Прямоугольник - это геометрическая фигура, которая имеет четыре стороны и четыре угла. Одна из особенностей прямоугольника заключается в том, что его противоположные стороны параллельны и равны друг другу.
Строение прямоугольника удобно изучать через его стороны, обозначенные буквами "а" и "б". Стоит отметить, что эти буквы являются произвольными обозначениями и зависят от контекста задачи или условия к изучаемому прямоугольнику.
В общем случае, стороны прямоугольника могут быть разными и определяться условиями задачи. Но также существует специальный тип прямоугольника, в котором стороны равны друг другу. Такой прямоугольник называется квадратом.
Если стороны прямоугольника обозначаются символами "а" и "б", то можно записать, что длина одной стороны равна "а", а длина другой стороны равна "б". Такое обозначение позволяет установить соотношение между сторонами прямоугольника и отобразить их в математической форме.
Размеры и свойства сторон прямоугольника

Стороны прямоугольника обозначаются буквами а и b. Часто сторона а называется основанием, а сторона b - высотой. Об этом говорят, когда речь идет о прямоугольнике, который образован линией, параллельной оси ординат и перпендикулярной оси абсцисс.
Строго говоря, значения сторон прямоугольника зависят от конкретного прямоугольника, поэтому мы не можем назначить точные числовые значения для сторон а и b. Однако можно сказать, что стороны прямоугольника всегда положительны и действительны числа.
Стороны прямоугольника могут быть равными или разными. Если стороны а и b равны, то прямоугольник является квадратом. Если стороны а и b разные, то прямоугольник является прямоугольником общего вида.
Зная значения сторон а и b, можно вычислить такие характеристики прямоугольника, как его периметр и площадь. Периметр прямоугольника равен сумме длин всех его сторон, а площадь равна произведению длины стороны а на длину стороны b.
Когда мы знаем значения сторон прямоугольника, мы также можем вычислить его диагонали. Длина главной диагонали равна квадратному корню из суммы квадратов сторон а и b, а длина побочной диагонали равна квадратному корню из разности квадратов сторон а и b.
Строение прямоугольника
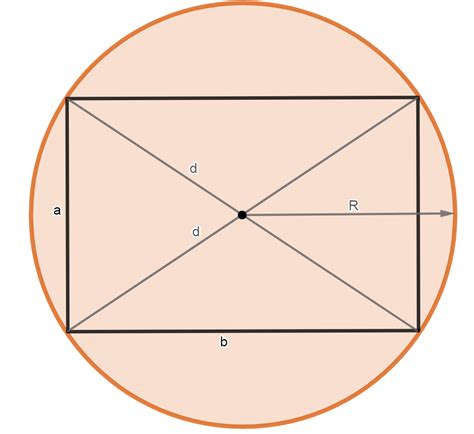
У прямоугольника всегда есть две пары сторон, противоположные друг другу и равные по длине. Обозначим эти стороны как стороны "а" и "b".
Стороны "а" и "b" могут быть любой длины в пределах, допустимых для прямоугольника. Длина стороны "а" может быть больше или меньше длины стороны "b", и наоборот.
Например, если сторона "а" равна 5 см, а сторона "b" равна 3 см, то мы можем сказать, что сторона "а" превышает сторону "b" на 2 см. Если же сторона "а" равна 3 см, а сторона "b" равна 5 см, то сторона "b" превышает сторону "а" на 2 см.
Таким образом, стороны прямоугольника "а" и "b" не имеют фиксированного значения, они могут быть любой длины, но всегда будут параллельны друг другу и иметь прямые углы.
Длина и ширина прямоугольника
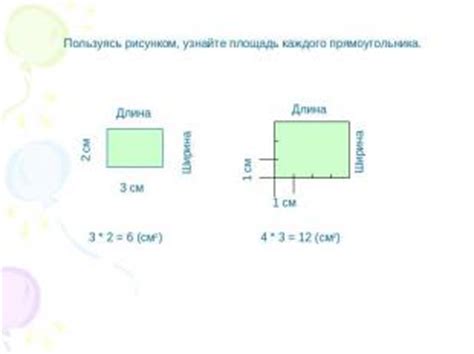
Длина прямоугольника - это размер, который измеряется в направлении, параллельном его длинной стороне. Чтобы измерить длину, необходимо провести линию от одного конца прямоугольника до другого.
Ширина прямоугольника - это размер, который измеряется в направлении, параллельном его короткой стороне. Чтобы измерить ширину, необходимо провести линию от одного края прямоугольника до другого.
Длина и ширина прямоугольника могут быть разными, т.е. не равны друг другу. Например, если длина равна 5 единицам, а ширина равна 3 единицам, то стороны прямоугольника равны 5 и 3 соответственно.
Длина и ширина прямоугольника влияют на его площадь и периметр. Для вычисления площади прямоугольника необходимо умножить его длину на ширину, а для вычисления периметра - сложить все его стороны.
Взаимосвязь между длиной и шириной

Когда мы говорим о прямоугольнике, нередко встает вопрос о взаимосвязи между его сторонами. Важно понимать, что длина и ширина прямоугольника тесно связаны друг с другом.
Для начала, необходимо отметить, что длину и ширину прямоугольника обычно измеряют в одних и тех же единицах измерения, например, в сантиметрах или метрах. Таким образом, стороны прямоугольника имеют общую меру и могут быть сравнимыми между собой.
Установить взаимосвязь между длиной и шириной прямоугольника можно с помощью математической формулы - "площадь прямоугольника равна произведению его длины на ширину". Или в более формальной записи:
S = а * b
Где:
S - площадь прямоугольника;
а - длина прямоугольника;
b - ширина прямоугольника.
Из этой формулы следует, что длина и ширина прямоугольника взаимосвязаны и являются существенными характеристиками фигуры. Если одна из сторон увеличивается, то площадь прямоугольника тоже увеличивается. А если одна из сторон уменьшается, то площадь прямоугольника также уменьшается.
Это свойство прямоугольников делает их очень удобными для решения различных задач, связанных с расчетом площадей и объемов. Благодаря взаимосвязи между длиной и шириной, можно легко определить, как изменится площадь прямоугольника при изменении длины или ширины.
Периметр прямоугольника
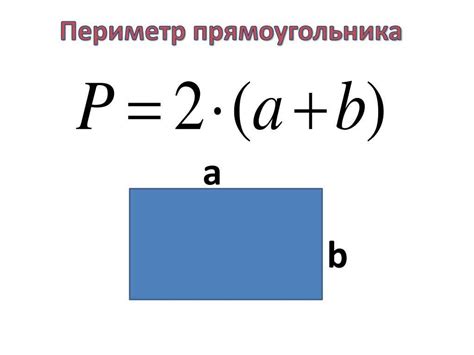
P = 2a + 2b
Или, что то же самое:
P = 2(a + b)
Таким образом, чтобы найти периметр прямоугольника, нужно знать длины его сторон и просто сложить их.
Площадь прямоугольника
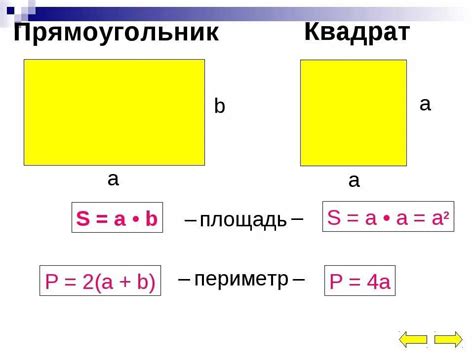
Площадь прямоугольника вычисляется по формуле:
S = а × б
Где а и б - стороны прямоугольника.
Чтобы вычислить площадь, необходимо знать значения обеих сторон. Первая сторона прямоугольника, обозначенная как а, указывает длину, а вторая сторона, обозначенная как б, указывает ширину. После того как значения сторон известны, достаточно перемножить их между собой, чтобы получить площадь прямоугольника.
Например, если длина прямоугольника равна 5 единицам, а ширина - 3 единицы, то площадь можно вычислить следующим образом:
S = 5 × 3 = 15
Таким образом, площадь прямоугольника со сторонами 5 и 3 равна 15 единицам.
Соотношение сторон прямоугольника
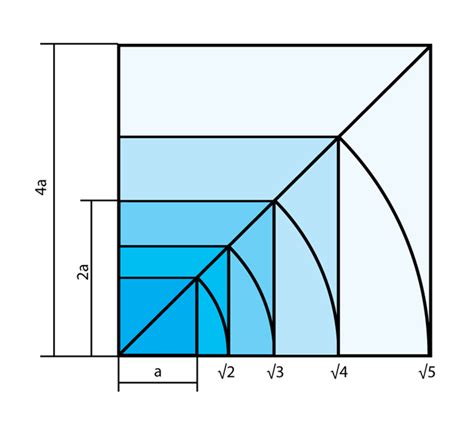
Соотношение сторон прямоугольника определяется отношением длины одной стороны к длине другой. Если обозначить длину одной стороны прямоугольника как "а", а длину другой стороны как "b", то соотношение сторон можно записать в виде "а:б" или "а/б".
Коэффициент пропорциональности между сторонами прямоугольника показывает, как изменяется одна сторона по отношению к другой. Например, если соотношение сторон прямоугольника равно 2:3, это означает, что одна сторона прямоугольника в 2 раза больше другой стороны.
Соотношение сторон прямоугольника может быть различным в зависимости от его формы и размеров. Однако, независимо от соотношения сторон, площадь прямоугольника всегда вычисляется как произведение длин его сторон: S = а * б.
Изучение соотношения сторон прямоугольника позволяет лучше понять его геометрические свойства и применять их в практических задачах.



