Промежутки возрастания и убывания функции являются важными концепциями в математике. Они позволяют нам анализировать поведение функции на определенном интервале и определять области, где значения функции увеличиваются или уменьшаются.
Промежуток возрастания функции - это интервал на оси x, на котором значения функции увеличиваются. Другими словами, если мы возьмем две точки на этом интервале, то значение функции во второй точке будет больше значения функции в первой точке. Чтобы найти промежутки возрастания, мы можем использовать производную функции.
Производная функции - это показатель скорости изменения функции в определенной точке. Если производная положительна в определенной точке, то функция возрастает в этой точке. Промежуток, на котором производная положительна, является промежутком возрастания функции. Мы также можем использовать монотонность функции для определения промежутка возрастания.
Промежуток убывания функции - это интервал на оси x, на котором значения функции уменьшаются. Если мы возьмем две точки на этом интервале, то значение функции во второй точке будет меньше значения функции в первой точке. Чтобы найти промежутки убывания, мы можем использовать производную функции.
Определение и характеристики
Промежуток возрастания функции - это интервал, на котором значение функции возрастает. То есть, если для любых двух точек x₁ и x₂ из этого интервала, выполняется неравенство f(x₁) < f(x₂), то говорят, что функция возрастает на данном промежутке.
Аналогично, промежуток убывания функции - это интервал, на котором значение функции убывает. Если для любых двух точек x₁ и x₂ из этого интервала, выполняется неравенство f(x₁) > f(x₂), то говорят, что функция убывает на данном промежутке.
Промежутки возрастания и убывания функции тесно связаны с производной функции. Для возрастания функции на интервале, производная должна быть положительной на этом интервале. Для убывания функции на интервале, производная должна быть отрицательной на этом интервале.
Промежутки возрастания и убывания функции могут быть как конечными, так и бесконечными. Они могут быть выражены в виде интервалов или использовать знаки бесконечности. Например, промежуток возрастания функции может быть записан как (a, b), где a и b - конечные числа, или как (a, +∞), если интервал бесконечный.
Изучение промежутков возрастания и убывания функции важно для понимания ее свойств и поведения. Они помогают определить экстремумы функции, промежутки строго возрастания или убывания, и многое другое.
Принципы поиска промежутков возрастания и убывания

Для определения промежутков возрастания и убывания функции необходимо учитывать изменение ее значения на заданном интервале.
Промежутки возрастания функции характеризуются тем, что значения функции на этих интервалах строго увеличиваются.
Для поиска промежутков возрастания необходимо выполнить следующие шаги:
- Вычислить первую производную функции.
- Решить неравенство f'(x) > 0.
- Найти интервалы, на которых производная строго положительна.
- Указать эти интервалы как промежутки возрастания функции.
Промежутки убывания функции отличаются тем, что значения функции на этих интервалах строго убывают.
Для поиска промежутков убывания необходимо выполнить следующие шаги:
- Вычислить первую производную функции.
- Решить неравенство f'(x) < 0.
- Найти интервалы, на которых производная строго отрицательна.
- Указать эти интервалы как промежутки убывания функции.
Помимо этого, необходимо также учитывать значения функции на границах интервалов, так как они могут влиять на результат.
Таким образом, принципы поиска промежутков возрастания и убывания функции сводятся к анализу производной и выявлению интервалов, на которых она положительна или отрицательна. Это позволяет наглядно представить изменение функции на заданном промежутке.
Как определить промежутки возрастания функции
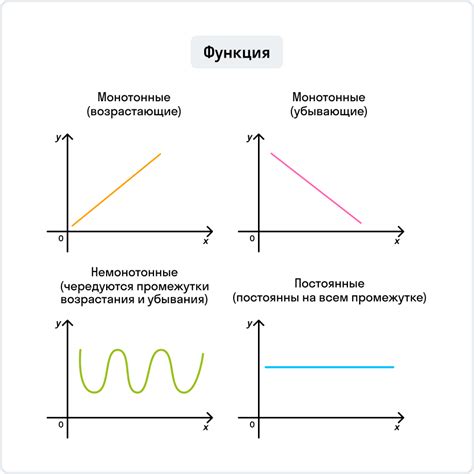
Для определения промежутков возрастания функции необходимо проанализировать ее производную. Промежуток называется возрастающим, когда значения производной положительны, то есть функция имеет положительную тенденцию роста на данном участке.
Чтобы найти промежутки возрастания функции, выполните следующие шаги:
- Найдите производную функции.
- Решите уравнение производной, приравняв его к нулю.
- Найдите значения х, для которых производная положительна (промежутки возрастания).
Примените полученные значения х для определения промежутков возрастания функции в исходной функции. Учитывайте, что функция может быть определена на различных участках, поэтому рассмотрите каждый из них отдельно.
Важно помнить, что промежутки возрастания функции являются лишь одной из характеристик функции и не дают полной картины ее поведения. Для полного анализа функции следует также оценивать ее монотонность, экстремумы, и другие аспекты.
Как определить промежутки убывания функции

Промежутки убывания функции можно определить, проанализировав ее производную на соответствующем интервале. Производная функции показывает наклон касательной к графику функции в каждой точке. Если значение производной отрицательно на каком-то интервале, то функция убывает на этом интервале.
Для определения промежутков убывания функции необходимо выполнить следующие шаги:
- Найти производную функции.
- Найти значения производной на интервалах, где функция определена и дифференцируема.
- Решить неравенство f'(x) < 0 для каждого интервала, где производная отрицательна.
Решение неравенства f'(x) < 0 даст нам интервалы, на которых функция убывает. Например, если решение неравенства имеет вид a < x < b, то на интервале (a, b) функция убывает.
Определение промежутков убывания функции имеет практическую значимость, так как это позволяет понять, как функция меняется при изменении аргумента. Это важно при решении задач оптимизации, поиске точек экстремума и анализе поведения функции в целом.
Примеры промежутков возрастания и убывания функции
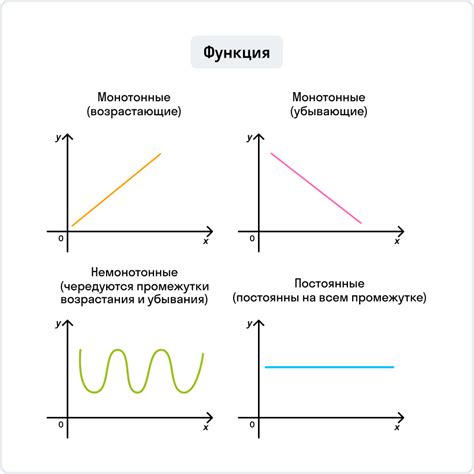
Например, функция f(x) = x^2 возрастает на всей числовой прямой (-∞, +∞), так как при увеличении x значение функции также увеличивается.
Промежуток убывания функции - это интервал, на котором значение функции убывает. В таком случае, график функции будет опускаться вниз.
Например, функция g(x) = -x^3 убывает на всей числовой прямой (-∞, +∞), так как при увеличении x значение функции уменьшается.
Промежутки возрастания и убывания функции могут также сменяться. Например, функция h(x) = x^2 - 3x + 2 возрастает на интервале (-∞, 1) и убывает на интервале (1, +∞).
Практическое применение промежутков возрастания и убывания

Одной из областей, где промежутки возрастания и убывания функций играют важную роль, является экономика. Анализ экономических данных и функций помогает предсказывать тренды и оптимизировать бизнес-процессы.
Например, в экономике, промежутки возрастания функции могут указывать на периоды роста спроса на товары или услуги. Это может быть полезной информацией для предпринимателей, которые могут адаптировать свои стратегии и решения соответственно.
Промежутки убывания функции, с другой стороны, могут указывать на периоды снижения спроса или рентабельности. Это может помочь предпринимателям принять важные решения, такие как сокращение издержек, изменение цен или пересмотр стратегии.
Промежутки возрастания и убывания также находят применение в физике, где функции могут описывать движение объектов или другие процессы. Например, знание промежутков возрастания функции скорости может помочь определить максимальную скорость движения тела и его ускорение.
В медицине промежутки возрастания и убывания могут использоваться для анализа изменения показателей здоровья пациента, таких как давление, пульс или уровень глюкозы в крови. Это может помочь врачам определить наличие патологических процессов и разработать оптимальный план лечения.
Использование промежутков возрастания и убывания функций также находит применение в анализе данных и машинном обучении. Анализируя промежутки функций, можно определить значимые точки или экстремумы, которые могут быть полезными при обработке данных или разработке моделей прогнозирования.
Таким образом, понимание и использование промежутков возрастания и убывания функций имеет широкий спектр практического применения, помогая нам лучше понять и описать мир вокруг нас, принимать обоснованные решения и разрабатывать эффективные стратегии в различных областях науки и бизнеса.



