Проекция вектора на координатную ось - это длина отрезка, проведенного из начала координат до точки, при которой этот отрезок перпендикулярен оси. Определение проекции вектора на ось является важным понятием в линейной алгебре и находит широкое применение в различных областях науки и инженерии.
Проекция вектора на ось часто используется для анализа направления движения объектов в физике и геометрии. Она позволяет определить, насколько объект движется вдоль оси, и является ключевым понятием при решении задач на векторное исчисление и механику. Проекция вектора на ось также может быть использована для определения угла между вектором и осью.
Приведем пример проекции вектора на ось. Пусть у нас есть вектор в трехмерном пространстве с координатами (3, 4, 5). Мы хотим найти проекцию этого вектора на ось x. Для этого мы должны найти длину отрезка, проведенного из начала координат до точки, на которой этот отрезок перпендикулярен оси x. В данном случае, проекция вектора на ось x будет равна 3, так как вектор имеет только одну ненулевую координату по оси x.
Проекция векторов на координатную ось
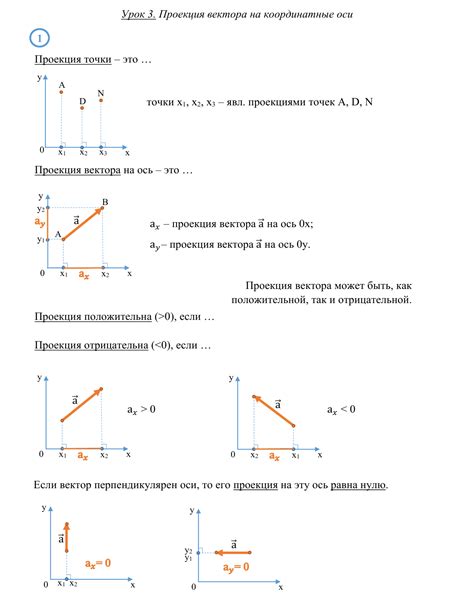
Для нахождения проекции вектора на ось необходимо умножить длину вектора на косинус угла между вектором и осью. Если вектор задан координатами (x, y, z), то его проекция на ось OX равна x, на ось OY - y, на ось OZ - z.
Например, рассмотрим вектор V = (3, 4, 5). Чтобы найти его проекцию на ось OX, нужно умножить x-координату вектора на единичный вектор OX. В данном случае, проекция на ось OX будет равна 3. Аналогично для осей OY и OZ.
Проекция векторов на координатные оси находит применение в решении различных задач. Например, в физике проекция вектора силы на оси системы координат может быть использована для нахождения работ, совершаемых вектором силы. В компьютерной графике, проекция вектора на экран может определить конечную позицию объекта при его движении.
Таким образом, проекция векторов на координатные оси является важным инструментом для анализа векторов и решения различных задач, связанных с их действием и перемещением.
| Ось | Проекция |
|---|---|
| OX | x |
| OY | y |
| OZ | z |
Определение проекции векторов на координатную ось
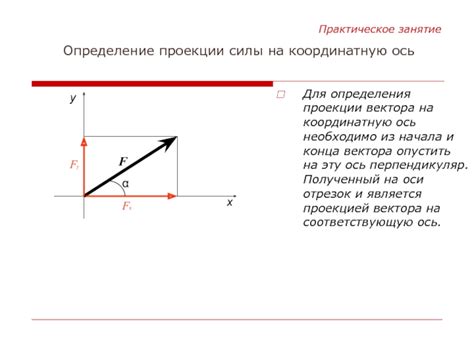
Проекции векторов на координатную ось представляют собой разложение векторов на компоненты, параллельные данной оси. Как известно, векторы могут быть представлены в виде направленных отрезков, их длина и направление определяются началом и концом вектора.
Проекции векторов на ось обычно обозначаются как Px (проекция на ось x), Py (проекция на ось y) и Pz (проекция на ось z) в трехмерном пространстве. Для двумерного пространства используется обозначение Px и Py.
Проекция вектора на определенную координатную ось является скалярной величиной, поскольку она представляет только длину вектора вдоль этой оси. Она рассчитывается с использованием скалярного произведения вектора и единичного вектора, направленного вдоль оси.
Проекция вектора V на ось a может быть рассчитана по формуле:
P = (V • a) / |a|
где V - вектор, а - ось, • - скалярное произведение, |a| - длина вектора a.
Зная проекции вектора на все три координатные оси, можно восстановить исходный вектор, объединив все проекции.
Примеры проекции векторов на координатную ось
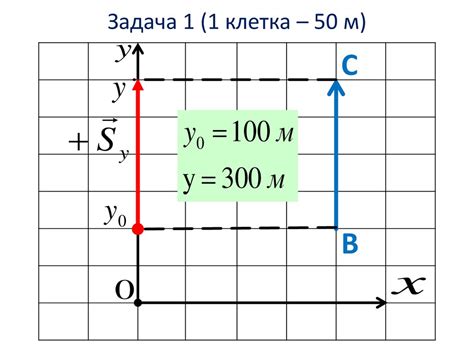
Проекция вектора на координатную ось представляет собой проекцию этого вектора на ось, параллельную этой оси. Такая проекция позволяет нам получить числовое значение, которое показывает, насколько вектор направлен вдоль данной оси.
Рассмотрим несколько примеров проекции векторов на ось:
1. Пусть у нас имеется вектор AB, заданный координатами A(2, 3) и B(4, 5). Для того чтобы получить проекцию этого вектора на ось Ox, необходимо проецировать каждую из координат точек A и B на эту ось. Таким образом, проекция вектора AB на ось Ox будет равна вектору CD, заданному координатами C(2, 0) и D(4, 0).
2. Рассмотрим вектор EF, заданный координатами E(1, 2) и F(3, 4). Проекция этого вектора на ось Oy будет равна вектору GH, который задан координатами G(0, 2) и H(0, 4).
3. Если вектор PQ задан координатами P(0, 0) и Q(-2, -3), то его проекция на ось Ox будет равна вектору RS, который задан координатами R(-2, 0) и S(-2, 0).
Таким образом, проекция вектора на координатную ось позволяет нам определить, в каком направлении и насколько велик вектор, если он направлен вдоль соответствующей оси. Это важный инструмент в линейной алгебре и нахождении числовых значений векторов.



