Деление чисел на 8 – одна из основных операций в арифметике, которую нам приходится выполнять ежедневно. Знание основных признаков и правил деления на 8 поможет нам справиться с этой задачей безошибочно и с минимальными затратами времени.
Основными признаками деления числа на 8 являются:
- Число делится на 8, если его последние три цифры являются кратными 8. Например, число 1328 делится на 8, так как последние три цифры – 328 – образуют кратное 8 число.
- Число делится на 8, если сумма его цифр является кратной 8. Например, число 376 делится на 8, так как его цифры 3 + 7 + 6 = 16, что делится на 8.
Правила деления на 8:
- Если число делится и на 2, и на 4, то оно делится и на 8. Например, число 984 делится и на 2, и на 4, а значит, оно делится и на 8.
- Если число заканчивается на 0, 8 или 4, то оно делится на 8. Например, числа 240, 728 и 856 все делятся на 8.
Знание признаков и правил деления на 8 позволяет производить эту операцию с уверенностью и точностью. Эти знания также могут быть полезными при решении других математических задач и применении арифметических навыков в повседневной жизни.
Признаки деления числа на 8
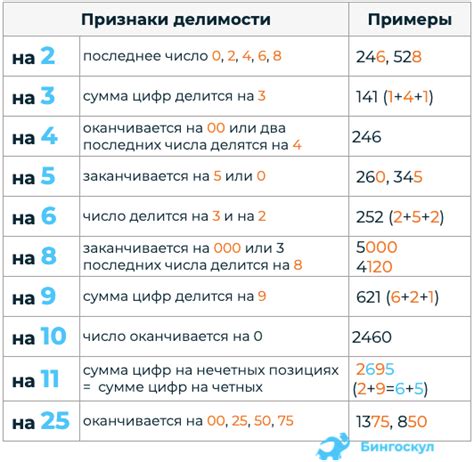
Деление чисел на 8 имеет свои особенности и признаки, которые позволяют определить, делится ли число на 8 без остатка. В данном разделе мы рассмотрим основные признаки и правила деления на 8.
- Признак деления на 8: последние три цифры числа образуют число, делящееся на 8 без остатка. Например, число 4328 делится на 8, так как 328 делится на 8 без остатка.
- Если число заканчивается на 0, 8 или 6, то оно делится на 8 без остатка. Например, число 560 делится на 8, так как последняя цифра 0 делится на 8 без остатка.
- Если сумма цифр числа делится на 8 без остатка, то само число также делится на 8 без остатка. Например, число 264 делится на 8, так как 2 + 6 + 4 = 12, что делится на 8 без остатка.
Зная эти основные признаки, можно легко определить, делится ли число на 8 без остатка. Это может быть полезно, например, при работе с большими числами или в задачах, где требуется определить кратность числа 8.
Основные признаки
При делении числа на 8 есть несколько основных признаков, которые помогут определить, делится ли число на 8 без остатка:
- Последние три цифры числа должны быть кратны 8. Если они кратны 8, то весь остаток от деления числа на 8 равен 0.
- Если сумма цифр числа, слева от последних трех цифр, кратна 8, то число делится на 8 без остатка. Например, число 1040 можно делить на 8, так как 1 + 0 + 4 = 5, что не кратно 8. А число 1048 можно делить на 8, так как 1 + 0 + 4 = 5, что кратно 8.
Таким образом, зная эти основные признаки, можно легко определить, делится ли число на 8 без остатка или нет. Эти признаки очень полезны, особенно при работе с большими числами, чтобы избежать лишних вычислений.
Правила деления на 8
Основные правила деления на 8 следующие:
- Число должно быть кратно 8. Если число не кратно 8, то его нужно расширить, добавив нули справа.
- Взять первые три разряда числа справа налево и проверить их делимость на 8. Если это число делится на 8 без остатка, то исходное число делится на 8.
- Если число не делится на 8, то нужно проверить левые разряды и продолжить этот процесс, пока не найдется число, которое делится на 8 без остатка.
- Если число оканчивается на ноль или является двузначным и делится на 8 без остатка, то исходное число тоже делится на 8 без остатка.
- Если число оканчивается на ноль или является двузначным и при делении на 8 дает остаток, то исходное число не делится на 8 без остатка.
Правила деления на 8 очень полезны в математике и помогают упростить процесс деления и получить точный результат. Они основаны на свойствах чисел и формулах, что позволяет эффективно выполнять деление и решать математические задачи, где требуется деление на 8.
Признаки делимости числа на 8
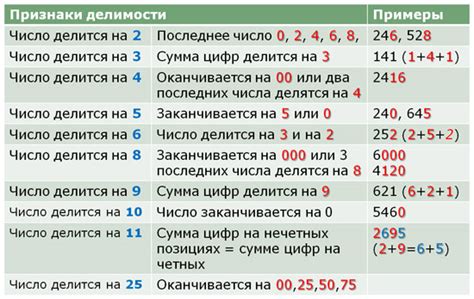
Основным признаком деления числа на 8 является то, что последние три цифры числа должны быть кратны 8. Если число удовлетворяет этому условию, то оно делится на 8 без остатка.
Также существуют правила деления на 8:
- Если число оканчивается на 0, 8 или 4, то оно делится на 8 без остатка.
- Если сумма цифр числа, умноженных на их разряды, делится на 8 без остатка, то и само число делится на 8.
Примеры:
- Число 248 делится на 8, так как последние три цифры (248) кратны 8.
- Число 360 делится на 8, так как оно оканчивается на 0 и сумма цифр (3 + 6 + 0) делится на 8.
- Число 573 не делится на 8, так как последние три цифры (573) не кратны 8.
Таким образом, признаки деления числа на 8 позволяют быстро определить, делится ли число на 8 без необходимости выполнения самого деления.
Признаки окончания числа на 8

Деление числа на 8 имеет свои особенности и признаки окончания, которые могут помочь в определении кратности числа этому делителю. При делении числа на 8, его последние три числа должны быть кратны 8, что можно проверить по следующим правилам:
| Последние три цифры числа | Признак окончания |
|---|---|
| 000 | Число кратно 8 |
| 008, 016, 024, 032, 040, 048, 056, 064, 072 | Число кратно 8 |
| 080, 088, 096, 104, 112, 120, 128, 136, 144 | Число кратно 8 |
| 152, 160, 168, 176, 184, 192, 200, 208, 216 | Число кратно 8 |
| 224, 232, 240, 248, 256, 264, 272, 280, 288 | Число кратно 8 |
| 296, 304, 312, 320, 328, 336, 344, 352, 360 | Число кратно 8 |
| 368, 376, 384, 392, 400, 408, 416, 424, 432 | Число кратно 8 |
| 440, 448, 456, 464, 472, 480, 488, 496 | Число кратно 8 |
| 504, 512, 520, 528, 536, 544, 552, 560 | Число кратно 8 |
| 568, 576, 584, 592, 600, 608, 616, 624 | Число кратно 8 |
| 632, 640, 648, 656, 664, 672, 680, 688 | Число кратно 8 |
| 696, 704, 712, 720, 728, 736, 744, 752 | Число кратно 8 |
| 760, 768, 776, 784, 792, 800, 808, 816 | Число кратно 8 |
| 824, 832, 840, 848, 856, 864, 872, 880 | Число кратно 8 |
| 888, 896, 904, 912, 920, 928, 936, 944 | Число кратно 8 |
| 952, 960, 968, 976, 984, 992 | Число кратно 8 |
Таким образом, если последние три цифры числа совпадают с одним из указанных в таблице, то число является кратным 8.
Правила деления больших чисел на 8
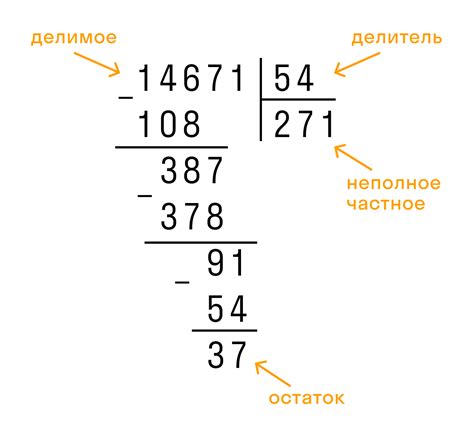
При делении больших чисел на 8 существуют особые правила и признаки, которые могут значительно упростить процесс деления. Вот основные правила, которых стоит придерживаться при делении чисел на 8:
1. Последние три цифры числа должны быть кратны 8.
Если последние три цифры числа кратны 8, то само число также будет кратно 8.
2. Исключение при делении чисел с единичным остатком.
Если число оканчивается на 1, 3, 5 или 7, то оно не делится на 8 без остатка.
3. Деление числа с нулевыми конечными цифрами.
Если числа оканчивается на 000, то оно делится на 8 без остатка. Это можно проверить, разделив все цифры числа на 8, и если получится число без десятичной части, то исходное число делится на 8.
4. Деление суммы чисел с нулевыми конечными цифрами.
Если числа оканчиваются на 000 и их сумма тоже оканчивается на 000, то эта сумма также делится на 8 без остатка.
Учитывая эти правила и признаки, деление больших чисел на 8 может быть очень простым и быстрым процессом.
Примеры деления чисел на 8
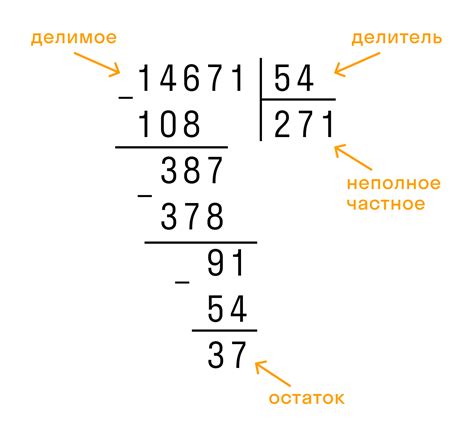
Пример 1:
Делимое: 48
48 ÷ 8 = 6
Остаток: 0
48 можно разделить на 8 без остатка.
Пример 2:
Делимое: 72
72 ÷ 8 = 9
Остаток: 0
72 также делится на 8 без остатка.
Пример 3:
Делимое: 56
56 ÷ 8 = 7
Остаток: 0
В случае числа 56, результатом деления на 8 также будет целое число без остатка.
Пример 4:
Делимое: 85
85 ÷ 8 = 10
Остаток: 5
В этом примере, при делении числа 85 на 8, результатом будет целое число 10, а остаток будет равен 5.
Таким образом, деление чисел на 8 позволяет быстро определить, можно ли разделить число на 8 без остатка, или какой будет остаток при делении. Этот навык может быть полезен при выполнении математических операций или при решении различных задач из реального мира.



