Математика - это невероятно интересная и разнообразная наука, которая помогает нам понять и описать мир вокруг нас. В ее рамках есть множество различных концепций и понятий, одним из которых является модуль числа.
Модуль числа представляет собой его абсолютное значение, то есть независимо от его знака. Например, модуль числа -5 равен 5, а модуль числа 8 равен 8. Именно поэтому модули часто используются для определения расстояний и величин, которые не могут быть отрицательными.
Противоположные числа - это пара чисел, которые находятся на равном расстоянии от нуля, но находятся по разные стороны от него. Например, противоположными числами являются -3 и 3, -10 и 10 и так далее.
Одна из интересных особенностей модулей противоположных чисел заключается в том, что их модули всегда одинаковы. Независимо от того, насколько большими или маленькими могут быть числа, их модули всегда равны. Это свойство помогает нам решать различные задачи и делает работу с числами более удобной и простой.
Особенности модулей противоположных чисел
Модуль числа представляет собой абсолютное значение числа, то есть его положительную величину.
Одной из особенностей модулей противоположных чисел является то, что модуль отрицательного числа равен модулю соответствующего положительного числа. Например, модуль числа -5 будет равен модулю числа 5, то есть оба эти числа имеют значение 5.
Еще одной особенностью модуля является его сокращенная запись. Вместо использования ключевого слова "модуль", часто используется символ "|" вокруг числа. Например, модуль числа -2 может быть записан как |-2|. Такая запись позволяет легче и более компактно обозначать модуль числа.
Модули противоположных чисел обладают следующим свойством: сумма модулей противоположных чисел равна нулю. Например, модуль числа -3 плюс модуль числа 3 будет равен 0, так как оба модуля имеют значение 3 и складываются в итоге в ноль.
Модули противоположных чисел также взаимодействуют с операциями сравнения. Например, модуль отрицательного числа всегда будет меньше, чем модуль положительного числа. Также, если модуль числа равен нулю, то само число является нулем. Например, модуль числа 0 равен 0.
Модули в математике

Модуль числа всегда является неотрицательным. Например, модуль числа 5 равен 5, а модуль числа -5 также равен 5.
Модуль числа можно выразить следующей формулой:
| Модуль числа х | = | { х, если х ≥ 0 |
|---|---|---|
| { -х, если х < 0 |
Модули используются в различных областях математики, физики и других наук. В геометрии, например, модуль вектора позволяет измерить его длину, без учета направления. В теории вероятностей модули используются для определения вероятности событий.
Особенности модулей могут быть полезными при решении различных математических задач. Например, модули противоположных чисел имеют одинаковые значения, что позволяет сократить вычисления и упростить работу с числами.
Изучение свойств модулей чисел позволяет более глубоко понять и использовать их в различных математических и физических задачах. Например, модуль разности двух чисел может быть использован для определения расстояния между этими числами на числовой прямой.
Противоположные числа
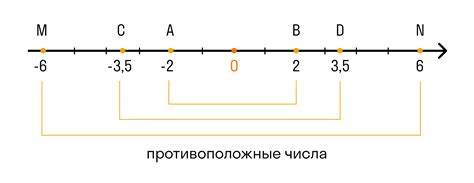
В математике противоположное число обозначается символом "−" (минус) перед числом. Если дано число x, его противоположное число будет −x.
Свойства противоположных чисел:
- Сумма противоположных чисел всегда равна нулю. Например, 5 + (-5) = 0.
- Умножение противоположных чисел всегда дает отрицательный результат. Например, 5 * (-5) = -25.
- Абсолютная величина противоположного числа совпадает с абсолютной величиной исходного числа. Например, |-5| = 5.
Противоположные числа используются в решении математических задач, а также в физике и других науках. Они позволяют удобно работать с отрицательными значениями и выражать противоположность различных величин.
Основные свойства модулей противоположных чисел

Определение модуля вводит понятие противоположного числа. Если a - это число, то -a называется противоположным числом к числу a.
Основные свойства модулей противоположных чисел:
- Модуль противоположного числа равен модулю данного числа: |a| = |-a|.
- Модуль произведения числа на -1 равен модулю данного числа: |-1 * a| = |a|.
- Модуль суммы двух чисел равен сумме модулей этих чисел: |a + b| = |a| + |b|.
- Модуль разности двух чисел равен разности модулей этих чисел: |a - b| = |a| - |b|.
Также стоит отметить, что модуль противоположного числа a всегда равен модулю самого числа a.
Применение модулей противоположных чисел

Модули противоположных чисел находят применение в различных областях науки и техники.
Одним из основных применений модулей противоположных чисел является решение задач, связанных с определением расстояния или разницы между двумя точками. Модуль разности двух чисел позволяет найти абсолютное значение этой разности, игнорируя ее знак. Например, в задачах геометрии, модули противоположных чисел могут быть использованы для определения расстояния между двумя точками на плоскости.
Модули противоположных чисел также широко используются в программировании. Они могут быть применены, например, для проверки условий или определения порядка событий. Модуль разности двух чисел может быть использован для определения того, какое из чисел больше или меньше. Такая проверка может быть полезной при написании программ, где нужно определить, выполнить ли определенное действие или нет.
В физике модули противоположных чисел могут быть использованы для определения величин, которые не зависят от их знака. Например, модуль определенного числа может представлять амплитуду колебаний или расстояние до объекта.



