Уравнения играют важную роль в математике и во многих других науках. Они позволяют нам описывать различные явления и взаимосвязи между переменными. Однако в уравнениях часто встречаются параметры, значения которых могут варьироваться. Важным вопросом является определение знака этих параметров. От чего же это зависит?
Существует несколько основных факторов, которые определяют знак параметров в уравнениях. Первый фактор - это физический или математический смысл параметра. Например, если параметр описывает массу объекта, то положительное значение будет означать, что масса объекта положительна, а отрицательное значение - что масса отрицательна, что может не иметь физического смысла. Таким образом, физические или математические законы могут задавать определенный знак параметра.
Второй фактор - это условия задачи или контекст, в котором рассматривается уравнение. Например, если решается задача о движении объекта, то параметр может обозначать его скорость. Если движение происходит вперед, то скорость будет положительной, а если назад - отрицательной. Это зависит от выбранной системы отсчета и описания направлений движения.
В конечном итоге значение параметров в уравнении зависит от его особенностей и контекста, в котором оно используется. Правильное определение знаков параметров является важным шагом в решении уравнений и позволяет получить правильный ответ на поставленную задачу.
Раздел 1: Значение параметров в уравнении

Знак параметров в уравнении зависит от нескольких основных факторов, которые определяются в контексте конкретной задачи. Рассмотрим основные из них:
| Фактор | Значение параметра |
|---|---|
| Физический смысл | Знак параметра может зависеть от физического значения, которое он имеет в данной задаче. Например, в уравнениях движения тела знак параметра может определять направление движения (положительное значение - движение вперед, отрицательное - движение назад). |
| Математическая модель | В некоторых математических моделях знак параметра может быть установлен заранее в соответствии с конвенцией или условием задачи. Например, в уравнении для нахождения корней квадратного уравнения знак перед квадратным корнем может быть установлен как "+", чтобы получить положительный корень. |
| Анализ данных | При анализе экспериментальных данных знак параметра может быть определен на основе полученных результатов. Например, если параметр отвечает за увеличение или уменьшение значения исследуемой величины, то его знак будет зависеть от направления изменения. |
Значение параметров в уравнении может быть как положительным, так и отрицательным в зависимости от указанных факторов. Поэтому важно учитывать контекст задачи и осознавать физический или математический смысл параметров при их определении.
Параметры и их влияние в уравнении

В уравнениях различных математических моделей, параметры играют важную роль и влияют на поведение системы. Знак параметров в уравнении зависит от нескольких основных факторов:
1. Физического значения параметра
В зависимости от физического значения параметра, его знак может быть положительным или отрицательным. Например, в уравнении движения материальной точки, масса материала может быть положительной величиной, так как масса не может быть отрицательной. Однако, в уравнении демпфированного колебания, коэффициент демпфирования может иметь как положительное, так и отрицательное значение, в зависимости от типа демпфирования.
2. Вида уравнения
В разных уравнениях зависимости между параметрами могут быть разными. Например, в уравнении роста популяции, параметр, описывающий прирост численности, будет иметь положительный знак, так как он увеличивает численность популяции. Однако, параметры, описывающие смертность или эмиграцию, могут иметь отрицательный знак, так как они уменьшают численность популяции. В уравнении реакции химической реакции, значения параметров также могут быть как положительными, так и отрицательными, в зависимости от типа реакции и ее направления.
3. Точки отсчета
В некоторых случаях, знак параметра в уравнении может зависеть от точки отсчета или системы отсчета, выбранной для математической модели. Например, при рассмотрении движения объекта вдоль оси координат, знак скорости объекта может меняться в зависимости от выбранного направления положительной оси.
Раздел 2: Константы и переменные
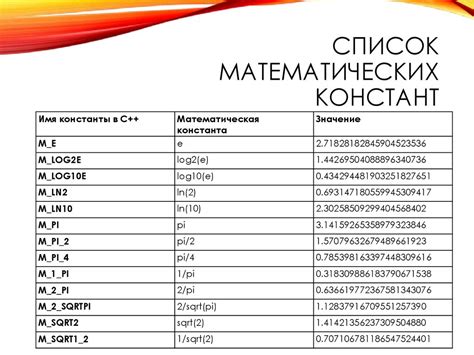
Переменные, в свою очередь, представляют собой неизвестные величины, которые мы пытаемся найти в процессе решения уравнения. Знак переменных также зависит от ситуации. В зависимости от поставленной задачи, переменные могут быть положительными или отрицательными.
Важно отметить, что знаки констант и переменных не всегда указываются явным образом в уравнении. Иногда мы можем определить их значения по контексту задачи или по условиям, которые включены в задачу. Поэтому при решении уравнений необходимо внимательно анализировать условия задачи и правильно определять знаки констант и переменных.
Чтобы решить уравнение и определить знак параметров, необходимо использовать математические методы и правила, которые позволяют найти корни уравнения. Корень уравнения - это значение переменной, при котором уравнение становится верным.
Роли констант и переменных в уравнении

Переменные, в свою очередь, представляют собой неизвестные значения, которые мы ищем при решении уравнения. В данном примере переменной является x. Значение переменной может быть различным в зависимости от конкретной ситуации.
Знаки параметров в уравнении зависят от роли констант и переменных. Константы могут быть положительными, отрицательными или нулевыми. Их знаки влияют на ход решения уравнения и определяют возможные значения переменных. Например, в уравнении 2x + 5 = 10 константа 5 положительна.
Переменные могут принимать разные значения и быть как положительными, так и отрицательными. Знак переменной в уравнении определяет, в каком направлении будет изменяться значение переменной при решении уравнения. Например, в уравнении -3x + 8 = 2 переменная x является отрицательной.
Таким образом, знаки параметров в уравнении играют важную роль в процессе решения и определяют допустимые значения переменных, а также направление и ход решения уравнения.
Раздел 3: Определение знака параметров
Определение знака параметров в уравнении зависит от нескольких факторов. Рассмотрим основные из них:
- Физический смысл параметра. Часто знак параметра в уравнении связан с его физическим смыслом. Например, если параметр отражает температуру, то положительное значение будет соответствовать повышению температуры, а отрицательное - понижению.
- Взаимосвязь с другими параметрами. Знак параметра может зависеть от взаимосвязи с другими параметрами в уравнении. Например, если изменение параметра приводит к увеличению другого параметра, то их знаки будут согласованы.
- Физические ограничения. Некоторые физические явления имеют определенные физические ограничения, которые могут определить знак параметра. Например, если параметр описывает массу объекта, то он не может быть отрицательным значением.
- Экспериментальные данные. Определение знака параметров часто происходит на основе экспериментальных данных. Анализ результатов эксперимента может позволить определить, какие знаки параметров соответствуют реальным явлениям.
- Математические модели. Использование математических моделей и уравнений может помочь определить знаки параметров. Например, анализ дифференциальных уравнений может показать, какие значения параметров приводят к положительным или отрицательным изменениям в системе.
Использование указанных факторов может помочь определить знак параметров и лучше понять, как изменения величин влияют на решение уравнения.
Методы определения знака параметров в уравнении

При решении уравнений, исследовании функций и анализе их графиков, очень важно определить знаки параметров в уравнении.
Существует несколько методов, которые позволяют определить знаки параметров:
1. Исследование знакопостоянства при определенных значениях аргумента. Для этого выбирают несколько значений аргумента и подставляют их в уравнение, а затем анализируют знак полученных значений функции. Если все значения положительные, то значки параметров будут одного знака, если все значения отрицательные, то будут другого знака.
2. Исследование поведения функции при аргументе стремящемся к бесконечности. Проверяют, как ведет себя функция при стремлении аргумента к бесконечности. Если функция возрастает или убывает при стремлении аргумента к бесконечности, то параметр будет иметь тот же знак.
3. Применение математических зависимостей и свойств. В некоторых случаях можно использовать математические зависимости и свойства функций, чтобы определить знаки параметров. Например, если параметр входит в уравнение с положительным знаком, то его знак будет зависеть от знака остальных параметров и функции в целом.
Знание методов определения знаков параметров в уравнении очень полезно при анализе математических моделей и решении различных задач. Оно позволяет более точно описывать и предсказывать поведение функций и их влияние на другие переменные.
Раздел 4: Взаимосвязь параметров

Знак параметров в уравнении может зависеть от нескольких факторов:
- Физического значения параметров: В зависимости от своей природы, параметры могут иметь положительное или отрицательное значение. Например, в уравнении движения тела в вертикальной плоскости, положительное значение параметра гравитации означает притяжение тела к земле, а отрицательное значение - отталкивание тела от земли.
- Математических условий задачи: В некоторых задачах может быть задано, что параметр должен быть положительным или отрицательным. Например, при решении квадратного уравнения может потребоваться найти только положительные корни. В таком случае знак параметра также будет положительным.
- Смысла переменных и других параметров: Возможно, что значения переменных и других параметров в уравнении могут указывать на то, какой знак должен быть у данного параметра. Например, если переменная, зависящая от параметра, имеет положительное значение, то можно предположить, что параметр тоже должен быть положительным.
Взаимосвязь между параметрами в уравнении может быть сложной и зависит от конкретной задачи. Важно учитывать все факторы, чтобы правильно определить знак параметров и достичь верных решений.
Как взаимосвязь параметров влияет на знак уравнения

Знак уравнения зависит от соотношения параметров, входящих в него. Взаимосвязь параметров может быть прямой или обратной, что определяет положительный или отрицательный знак уравнения.
При прямой взаимосвязи параметров, увеличение одного из них приводит к увеличению знака уравнения. Например, при увеличении положительного параметра, знак уравнения сохраняет свой знак: если уравнение было положительным, то оно остается положительным, и наоборот.
Если же взаимосвязь параметров обратная, то увеличение одного из них приводит к изменению знака уравнения. Например, увеличение отрицательного параметра может изменить знак уравнения с отрицательного на положительный или наоборот.
Также следует учесть, что уравнение может содержать несколько параметров, взаимосвязь которых может быть сложной. В этом случае изменение одного параметра может привести к изменению знаков других параметров и, как следствие, знака всего уравнения.
Поэтому при анализе уравнения необходимо учитывать взаимосвязь параметров и применять соответствующие методы и подходы для определения их влияния на знак уравнения.



