Векторы – это математические объекты, которые характеризуются не только своей величиной, но и направлением. Сложение векторов – одна из основных операций, которая позволяет находить результат суммы двух или более векторов.
Для сложения векторов применяется так называемое правило параллелограмма. Согласно этому правилу, если имеются два вектора, то их сумма будет равна вектору, который образует диагональ параллелограмма, построенного на этих векторах.
Рассмотрим пример. Пусть имеются два вектора: A и B. Вектор A задан своей длиной и углом с некоторой опорной осью, вектор B – своей длиной и углом с той же опорной осью. Для сложения векторов A и B нужно применить правило параллелограмма: отложить от начала координат вектор A и вести из его конца вектор B. Тогда диагональ параллелограмма, образованная из векторов A и B, будет искомым результатом – суммой векторов A и B.
Что такое векторы?
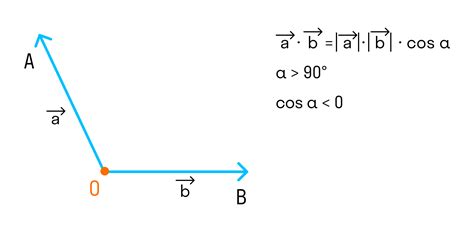
Векторы могут быть представлены в виде стрелок, где направление стрелки указывает на направление вектора, а длина стрелки соответствует величине вектора. Они могут быть двухмерными (состоять из двух компонентов) или трехмерными (состоять из трех компонентов).
Основные свойства векторов:
| Свойство | Описание |
|---|---|
| Направление | Векторы имеют определенное направление, которое указывается со стрелкой. |
| Длина | Величина вектора определяется его длиной, которая обозначает силу или мощность вектора. |
| Сложение | Векторы могут быть сложены вместе, чтобы получить новый вектор. Это выполняется путем суммирования соответствующих компонентов векторов. |
| Вычитание | Векторы могут быть вычтены друг из друга, чтобы получить новый вектор. Это выполняется путем вычитания соответствующих компонентов векторов. |
| Умножение на скаляр | Векторы могут быть умножены на скаляр (число), чтобы получить новый вектор, длина и направление которого будут изменены. |
Примеры применения векторов:
- В физике, векторы используются для описания силы, скорости и ускорения объектов.
- В геометрии, векторы используются для определения координат точек в пространстве и решения геометрических задач.
- В компьютерной графике, векторы используются для представления позиции и направления объектов на экране.
Сложение векторов: основные принципы

- Коммутативность: порядок слагаемых не влияет на результат сложения. То есть, вектор a + вектор b равно вектору b + вектор a.
- Ассоциативность: при сложении трех или более векторов, результат не зависит от порядка их суммирования. То есть, (вектор a + вектор b) + вектор c равно вектору а + (вектор b + вектор c).
- Уникальность нулевого вектора: сумма вектора и нулевого вектора равна исходному вектору. То есть, вектор a + 0 = вектор a.
- Существование противоположного вектора: для каждого вектора существует вектор с противоположным направлением и такой же длиной, сумма которого с исходным вектором равна нулевому вектору. Иными словами, для вектора a существует вектор -a, такой что a + (-a) = 0.
Векторы могут быть представлены с помощью различных методов, например, в виде графических стрелок или в виде упорядоченных наборов чисел, называемых компонентами. Для сложения векторов в виде компонент необходимо сложить соответствующие компоненты каждого вектора.
Принципы сложения векторов могут быть наглядно проиллюстрированы с помощью таблицы:
| Вектор A | Вектор B | Вектор A + B |
|---|---|---|
| 2 | 3 | 5 |
| -1 | 4 | 3 |
В данной таблице представлены два вектора A и B, их компоненты и результат их сложения вектор A + B.
Важно отметить, что сложение векторов может быть использовано не только для определения суммы двух векторов, но и для определения результатантного вектора, который представляет собой сумму всех векторов в системе.
Графический метод сложения векторов

Для визуализации сложения векторов достаточно нарисовать два вектора, начиная с одной точки и указав их направления и длины. Затем, используя правило параллелограмма, проводятся соответствующие стороны и диагонали параллелограмма. Вектор, соединяющий начало и конец диагонали, будет результатом сложения исходных векторов.
| Шаг | Описание | Пример |
|---|---|---|
| 1 | Начните с рисования первого вектора, задав его направление и длину. |  |
| 2 | Из начала первого вектора постройте второй вектор, указав его направление и длину. |  |
| 3 | Постройте параллелограмм, используя начало первого вектора, начало второго вектора и конец первого вектора. |  |
| 4 | Проведите диагональ параллелограмма от начала второго вектора до конца первого вектора. |  |
| 5 | Вектор, соединяющий начало и конец диагонали, является результатом сложения исходных векторов. |  |
Графический метод сложения векторов позволяет наглядно представить результат сложения исходных векторов и использовать его в решении задач из различных областей, таких как физика, геометрия и другие.
Алгебраический метод сложения векторов

Для применения алгебраического метода сложения векторов необходимо знать их компоненты. Компоненты вектора могут быть представлены числами или переменными и обозначаются обычно буквами с индексами. Например, вектор A может быть представлен в виде а = (a1, a2, a3), где a1, a2, a3 - компоненты вектора A.
Чтобы сложить два вектора с использованием алгебраического метода, нужно сложить соответствующие компоненты каждого вектора по отдельности. Например, чтобы сложить векторы A и B с компонентами a1, a2, a3 и b1, b2, b3 соответственно, получим новый вектор C с компонентами c1, c2, c3, где c1 = a1 + b1, c2 = a2 + b2, c3 = a3 + b3.
Алгебраический метод сложения векторов позволяет работать с векторами в виде алгебраических объектов, что значительно упрощает вычисления и позволяет получить точные значения для суммы векторов.
Примеры сложения векторов в графическом и алгебраическом виде
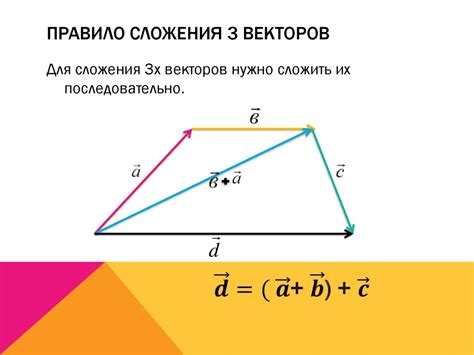
Графическое представление сложения векторов основано на использовании стрелок, где начальная точка первого вектора выступает в качестве начальной точки второго вектора. Затем конечная точка первого вектора становится начальной точкой итогового вектора. Таким образом, итоговый вектор представляет собой прямую от начальной точки первого вектора до конечной точки последнего вектора.
Например, если у нас есть два вектора: AB и BC, где вектор AB имеет направление на север, а вектор BC имеет направление на восток, то результатом сложения этих векторов будет вектор AC, который будет иметь направление на северо-восток.
Алгебраическое представление сложения векторов основано на их координатах. Каждый вектор представлен в виде упорядоченной пары чисел (x, y), где x - горизонтальная составляющая вектора, а y - вертикальная составляющая вектора. Для сложения векторов их соответствующие составляющие складываются по отдельности, чтобы получить итоговые составляющие итогового вектора.
Например, если у нас есть два вектора: AB = (2, 3) и BC = (4, -1), то итоговым вектором будет AC = AB + BC = (6, 2).
- Сложение векторов может быть представлено как графически, так и алгебраически.
- Графическое представление основывается на использовании стрелок и начальных и конечных точек векторов для построения итогового вектора.
- Алгебраическое представление основывается на сложении горизонтальных и вертикальных составляющих векторов для получения итоговых составляющих.
- В обоих случаях результат сложения векторов - это новый вектор, объединяющий характеристики исходных векторов.
Умножение вектора на число: суть и примеры

Для умножения вектора на число, каждая компонента вектора умножается на это число отдельно. Например, для вектора 𝜃 = (2, 3), умножение на 2 даёт вектор 𝜃 = (4, 6) и умножение на -3 даёт вектор 𝜃 = (-6, -9).
Умножение вектора на число имеет широкое применение в различных областях, включая физику, информатику и экономику. Например, векторы могут представлять силы или скорости, и умножение на число позволяет изменять их интенсивность или масштаб.
Условия коммутативности и ассоциативности сложения векторов

Условие коммутативности гласит, что порядок слагаемых не влияет на результат сложения векторов. То есть, для любых векторов A и B справедливо равенство:
| A + B = B + A |
|---|
| где A и B - векторы |
Это означает, что если мы поменяем местами слагаемые, результат сложения не изменится.
Условие ассоциативности гласит, что при сложении трех векторов порядок скобок не имеет значения. То есть, для любых векторов A, B и C справедливо равенство:
| (A + B) + C = A + (B + C) |
|---|
| где A, B и C - векторы |
Это означает, что можно сначала сложить два произвольных вектора, а затем прибавить к результату третий вектор, или можно сначала прибавить первый вектор ко второму, а затем сложить получившуюся сумму с третьим вектором - результат будет одинаковым.
Знание условий коммутативности и ассоциативности сложения векторов позволяет упростить вычисления и дает возможность менять порядок операций без изменения результата.



