Ядро и образ линейного оператора – это ключевые понятия в линейной алгебре, которые играют важную роль в понимании и исследовании линейных преобразований и их свойств.
Ядро линейного оператора обозначается как $\ker(T)$ (от немецкого "керн", что означает "ядро") и представляет собой множество всех векторов, которые проецируются оператором в ноль или, другими словами, не изменяются под его действием. То есть, если $\mathbf{x} \in \ker(T)$, то оператор $T$ при действии на вектор $\mathbf{x}$ превращает его в нулевой вектор $\mathbf{0}$. Ядро линейного оператора является линейным подпространством и может быть интерпретировано как множество всех решений однородного уравнения $T(\mathbf{x}) = \mathbf{0}$.
Образ линейного оператора обозначается как $\operatorname{Im}(T)$ (от англ. "image", что означает "образ") и представляет собой множество всех векторов, в которые можно преобразовать исходные векторы оператором $T$. То есть, если $\mathbf{y} \in \operatorname{Im}(T)$, то существует вектор $\mathbf{x}$ такой, что $T(\mathbf{x}) = \mathbf{y}$. Образ линейного оператора является линейным подпространством и может быть интерпретировано как множество всех возможных значений оператора $T$.
Рассмотрим пример. Пусть линейный оператор $T$ действует на пространстве $\mathbb{R}^3$ и имеет матрицу $A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$. Необходимо найти ядро и образ оператора $T$. Для этого решим уравнение $T(\mathbf{x}) = \mathbf{0}$. Для нахождения образа оператора $T$ применим оператор к базисным векторам пространства $\mathbb{R}^3$ и запишем их линейные комбинации.
Что такое ядро и образ линейного оператора?
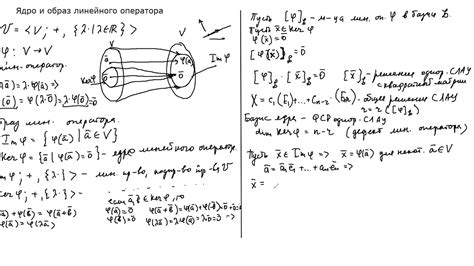
Ядро линейного оператора - множество векторов, которые отображаются в нулевой вектор. Другими словами, ядро содержит все векторы, на которые оператор действует их вектор нуля. Обозначается как Ker(T) или N(T), где T - сам оператор.
Образ линейного оператора - множество всех векторов, в которые может быть отображен исходный вектор. Образ линейного оператора является подпространством целевого векторного пространства. Обозначается как Im(T) или R(T).
Ядро и образ линейного оператора связаны друг с другом. В частности, ядро является подпространством исходного векторного пространства, а образ является подпространством целевого векторного пространства. Также справедлива размерность образа, которая равна разности размерности целевого векторного пространства и размерности ядра.
Знание ядра и образа линейного оператора помогает в анализе его свойств, например, определении его инъективности (инъективный оператор имеет тривиальное ядро) или сюръективности (сюръективный оператор имеет образ, совпадающий с целевым векторным пространством).
Примеры использования ядра и образа линейного оператора включают решение линейных систем уравнений, нахождение базиса векторного пространства, анализ графа связей в задачах оптимизации и многих других математических и научных областях.
Основы работы с ядром линейного оператора
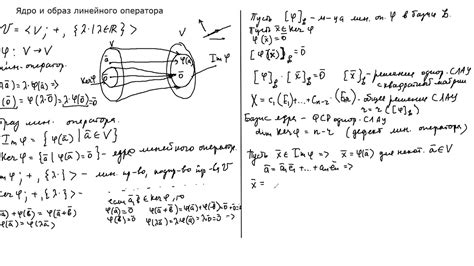
Работа с ядром линейного оператора важна для понимания его свойств и возможностей. В частности, ядро позволяет установить, есть ли нетривиальные решения у линейных уравнений, связанных с оператором.
Для работы с ядром линейного оператора можно использовать следующие основные шаги:
- Найти все векторы, на которых оператор превращается в нулевой вектор. Для этого нужно решить уравнение A(x) = 0, где A - матрица оператора, x - вектор.
- Составить базис ядра. Это набор линейно независимых векторов, которые образуют ядро оператора.
- Определить размерность ядра. Размерность ядра равна количеству векторов в базисе.
Работа с ядром линейного оператора позволяет понять его сущность и дает возможность решать различные задачи линейной алгебры, связанные с оператором.
Применение ядра линейного оператора: примеры

Пример 1: Линейные системы уравнений
Рассмотрим систему линейных уравнений вида Ax = 0, где A - матрица коэффициентов, а x - вектор неизвестных. Чтобы найти решение этой системы, необходимо найти ядро линейного оператора A. Ядро линейного оператора в данном случае представляет собой множество всех решений системы уравнений Ax = 0. Знание ядра линейного оператора позволяет определить все возможные решения системы и понять, существует ли ненулевое решение.
Пример 2: Сжатие данных
В области обработки сигналов и сжатия данных использование ядра линейного оператора может быть очень полезно. Например, можно использовать ядро линейного оператора для нахождения главных компонент (principal components) в многомерных данных. Главные компоненты представляют собой линейные комбинации исходных признаков, которые содержат максимально возможное количество информации. Нахождение ядра линейного оператора в данном случае позволяет снизить размерность данных, сохраняя при этом значимую информацию.
Пример 3: Разложение матрицы
Ядро линейного оператора также может быть использовано для разложения матрицы на сумму двух подматриц. В этом случае ядро линейного оператора представляет собой множество всех линейных комбинаций столбцов матрицы, которые равны нулю. Разложение матрицы с использованием ядра линейного оператора может быть полезно при решении систем линейных уравнений, а также в других задачах линейной алгебры.
| Пример | Применение ядра линейного оператора |
|---|---|
| Линейные системы уравнений | Нахождение решений системы уравнений Ax = 0 |
| Сжатие данных | Нахождение главных компонент в многомерных данных |
| Разложение матрицы | Разделение матрицы на две подматрицы |
Понятие образа линейного оператора и его свойства

Свойства образа линейного оператора:
- Образ линейного оператора всегда является подпространством векторного пространства, в котором определен оператор.
- Образ линейного оператора может быть нулевым пространством, если все векторы из области определения преобразуются в нулевой вектор.
- Образ линейного оператора может совпадать с векторным пространством, в котором определен оператор, если пространство полностью заполняется его образами.
- Размерность образа линейного оператора не превышает размерность векторного пространства, в котором определен оператор.
- Если размерность образа линейного оператора равна размерности векторного пространства, то образ является всем векторным пространством.
Образ линейного оператора играет важную роль в линейной алгебре и может использоваться для анализа и решения различных задач в математике и прикладных науках.
Пример:
Рассмотрим линейный оператор, заданный матрицей:
$$
A =
\begin{pmatrix}
2 & 1 & 3 \\
1 & 0 & 2 \\
3 & 2 & 5 \\
\end{pmatrix}
$$
Область определения этого оператора состоит из всех трехмерных векторов, а векторами являются столбцы данной матрицы. Пусть вектор $$\mathbf{v}$$ является произвольным вектором из этой области определения.
Применяя линейный оператор к вектору $$\mathbf{v}$$, получим новый вектор $$\mathbf{w}$$, который будет являться образом данного оператора для вектора $$\mathbf{v}$$. Множество всех векторов-образов будет образовывать образ линейного оператора.
Используя данную матрицу, мы можем найти образ линейного оператора путем умножения матрицы на каждый вектор из области определения. Таким образом, мы можем найти множество всех векторов-образов.
Образ линейного оператора может быть использован для определения свойств оператора, нахождения его ранга, а также для решения системы линейных уравнений и других задач линейной алгебры.
Примеры работы с образом линейного оператора

Для наглядности рассмотрим несколько примеров работы с образом линейного оператора:
- Пусть дан линейный оператор A: R^3 -> R^2, который преобразует трехмерные векторы в двумерные. Образ оператора A - это все возможные двумерные векторы, которые можно получить путем применения оператора A к трехмерным векторам.
- Рассмотрим линейный оператор B: R^2 -> R^2, который осуществляет поворот вектора на 90 градусов по часовой стрелке. Образ оператора B будет представлять собой все возможные векторы, которые можно получить путем поворота любого двумерного вектора на 90 градусов по часовой стрелке.
- Пусть имеется линейный оператор C: R^3 -> R^2, который проецирует трехмерные векторы на плоскость XY, игнорируя координату по оси Z. Образ оператора C будет представлять собой все двумерные векторы, полученные при проецировании трехмерных векторов на плоскость XY.
Это лишь несколько примеров работы с образом линейного оператора. В каждом случае образ оператора будет зависеть от его конкретного определения и действия, осуществляемого на векторы.
Понимание образа линейного оператора позволяет анализировать его свойства и осуществлять различные преобразования и операции с векторами.



