Кратные числа - это числа, которые делятся на другое число без остатка. В курсе математики в 5 классе дети начинают знакомиться с понятием кратных чисел и учатся определять их с помощью особых правил.
Для понимания этого понятия важно знать, что каждое натуральное число имеет бесконечно много кратных чисел. Например, число 2 имеет бесконечное количество кратных чисел: 4, 6, 8, 10 и т.д.
Определить, является ли число кратным заданному числу, можно с помощью такого правила: если остаток от деления числа на данное число равен нулю, то число является кратным. Например, число 15 является кратным числу 3, так как 15 делится на 3 без остатка.
Определение кратных чисел
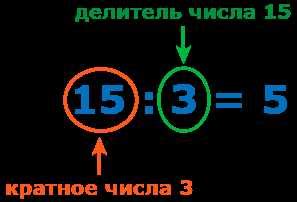
Для определения кратности числа A числу B, необходимо проверить, делится ли число A на число B без остатка. Если деление происходит без остатка, то число A является кратным числом числа B, в противном случае - не является.
Например, для числа 6 кратными числам будут: 1, 2, 3 и 6. Поскольку 6 делится на все эти числа без остатка.
Кратные числа имеют ряд свойств. Например, если число A является кратным числу B, то число B является делителем A. Также, если число A является кратным числу B, то число A также является кратным числу, на которое делится число B.
Примеры кратных чисел

Давайте рассмотрим некоторые примеры кратных чисел:
Пример 1: Число 10. Его кратными будут числа 0, 10, 20, 30 и т.д.
Пример 2: Число 3. Его кратными будут числа 0, 3, 6, 9 и т.д.
Пример 3: Число 7. Его кратными будут числа 0, 7, 14, 21 и т.д.
Кратные числа могут быть положительными и отрицательными. Например, для числа 5 его кратными будут числа -5, 0, 5, 10 и т.д.
Запомните, что для определения кратных чисел нужно смотреть, делится ли число на заданное число без остатка. Если делится без остатка, то оно является кратным числом, в противном случае - не кратным.
Правила определения кратных чисел

- Число, которое делится на какое-то другое число без остатка, называется кратным этому числу.
- То число, на которое делится другое число, называется делителем.
- Одинаковым делителем для двух чисел является их наименьший общий делитель.
Например, число 15 является кратным числу 3, так как 15 делится на 3 без остатка. Также 15 является кратным числу 5, потому что 15 делится на 5 без остатка.
Одинаковым делителем для чисел 15 и 25 является число 5, а для чисел 15 и 9 - число 3.
Зная эти правила, вы сможете легко определить, является ли одно число кратным другому и найти их общий делитель.
Кратные числа являются важным понятием в математике, и их изучение поможет вам лучше понять взаимосвязи чисел и различные математические операции.



