Геометрия - одна из важнейших наук, изучающая пространственные и фигурные отношения между объектами. Одним из основных понятий геометрии являются образ и прообраз. Образ и прообраз - это два взаимно обратных понятия, тесно связанных с понятием функции.
Образ - это результат применения функции к некоторому объекту. Например, если функция описывает отображение точек плоскости, то образом может быть другая точка плоскости. Образ может быть сконструирован по различным правилам и законам, заложенным в функции. Он является результатом применения функции и может иметь различную геометрическую интерпретацию.
Прообраз, напротив, является объектом, который после применения функции становится образом. Он является исходным объектом, который задает функцию и определяет ее действие. Прообраз может быть точкой, прямой или другой геометрической фигурой, которая подвергается отображению. Понимание прообраза играет важную роль в процессе понимания функций и их геометрической интерпретации.
Что такое геометрия и для чего она нужна?

Цель геометрии - понять и объяснить фундаментальные законы и принципы, которые управляют формой и структурой реального мира. Геометрия помогает нам развивать представление о пространстве, в котором мы живем, и понимать, как оно устроено.
Геометрия используется в различных областях науки и техники. Например, в архитектуре геометрия позволяет проектировать здания с определенными формами и пропорциями, которые обладают эстетической и функциональной ценностью. В физике геометрические концепции используются для описания движения тел и взаимодействия частиц. В компьютерной графике геометрия используется для создания реалистичных трехмерных моделей и анимаций.
Геометрия также развивает абстрактное мышление, логику и аналитические навыки. Она помогает развить способность анализировать форму и структуру объектов, решать проблемы и находить новые способы решения задач. Геометрические рассуждения часто используются в математических и логических задачах, а также в повседневной жизни, например, при планировании пространства или строительстве.
Таким образом, геометрия является неотъемлемой частью нашей жизни и играет важную роль в понимании мира вокруг нас. Она позволяет нам визуализировать и анализировать пространственные объекты и помогает развить важные когнитивные навыки, которые применимы в различных сферах деятельности.
Чем образ отличается от прообраза?

Образ - это результат применения какого-либо преобразования или отображения к исходному объекту. В случае геометрических фигур, образ может быть получен путем их поворота, отражения, масштабирования и т.д. Образ содержит точно такие же элементы исходного объекта, но может иметь другую форму, положение или размер.
Прообраз - это исходный объект, который является исходной точкой перед преобразованием или отображением. Прообраз содержит исходное положение, форму и размер. Он может быть использован для получения образа путем применения соответствующего преобразования или отображения.
Основное отличие между образом и прообразом заключается в том, что образ - это результат преобразования или отображения, тогда как прообраз - это исходный объект, который используется для получения образа. Образ отражает изменения, которые произошли с исходным объектом, в то время как прообраз остается без изменений.
Примеры образов и прообразов в геометрии

Пример 1: Поворот
Пусть имеется прямоугольник ABCD с координатами вершин:
A(0, 0), B(4, 0), C(4, 2), D(0, 2).
Если осуществить поворот прямоугольника относительно точки O(0, 0) на 90 градусов по часовой стрелке, то получим новый прямоугольник A'B'C'D':
A'(0, 0), B'(0, 4), C'(2, 4), D'(2, 0).
Здесь прямоугольник ABCD является образом, а A'B'C'D' - прообразом.
Пример 2: Отражение
Рассмотрим треугольник ABC с координатами вершин:
A(0, 0), B(3, 0), C(0, 2).
Если осуществить отражение треугольника относительно оси OY, то получим новый треугольник A'B'C':
A'(0, 0), B'(-3, 0), C'(0, 2).
Здесь треугольник ABC является образом, а A'B'C' - прообразом.
Пример 3: Растяжение
Рассмотрим прямоугольник ABCD с координатами вершин:
A(0, 0), B(4, 0), C(4, 2), D(0, 2).
Если увеличить координаты каждой вершины прямоугольника в 2 раза, то получим новый прямоугольник A'B'C'D':
A'(0, 0), B'(8, 0), C'(8, 4), D'(0, 4).
Здесь прямоугольник ABCD является образом, а A'B'C'D' - прообразом.
Это лишь несколько примеров из множества возможных образов и прообразов в геометрии. Понимание этих понятий позволяет прояснить связь между исходным пространством и его отображением, а также обнаружить закономерности и особенности преобразований.
Какие свойства имеют образы и прообразы?

Свойства образов и прообразов зависят от типа преобразования, которое применяется. Вот некоторые основные свойства:
- Сохранение длин и углов: Некоторые преобразования, например, параллельное перенос и поворот, сохраняют длины отрезков и величины углов. Это значит, что образ фигуры будет иметь те же длины и углы, что и исходная фигура.
- Изменение размеров: Некоторые преобразования, такие как сжатие или растяжение, изменяют размеры фигуры. Образ будет иметь другие длины и углы, чем исходная фигура.
- Инверсия: Некоторые преобразования меняют ориентацию фигуры, например, отражение относительно прямой. Образ будет "зеркальным отражением" исходной фигуры.
- Сохранение параллельности и перпендикулярности: Некоторые преобразования сохраняют параллельность линий и перпендикулярность отрезков, например, параллельное перенос и отражение относительно оси.
Использование понятий образа и прообраза в решении задач

В задачах на определение образа и прообраза, необходимо учитывать тип преобразования. Например, при рассмотрении преобразования как отражение относительно прямой, нужно найти образ исходного объекта, исходя из его симметричного положения относительно заданной прямой. В таких задачах используется таблица с двумя столбцами - исходный объект и его образ.
| Исходный объект | Образ |
|---|---|
| Точка A | Точка A' |
| Прямая BC | Прямая B'C' |
| Отрезок DE | Отрезок D'E' |
Другой пример использования понятий образа и прообраза - задачи на нахождение прообраза в результате преобразования. Например, если заданы координаты точки B' после сдвига на вектор (3, 4), то необходимо найти исходную точку B. Для решения таких задач используется обратное преобразование, которое позволяет найти исходный объект по его образу.
Таким образом, понятия образа и прообраза играют важную роль в геометрии и позволяют решать разнообразные задачи по отображению и преобразованию геометрических объектов.
Образы и прообразы в преобразованиях геометрических фигур
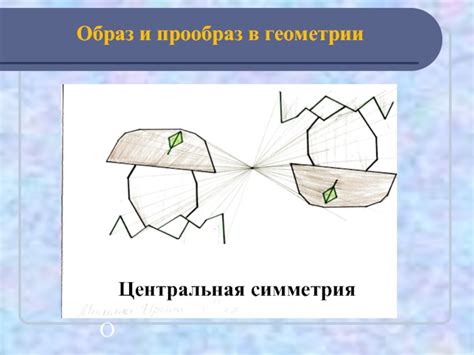
Образом точки, отрезка, фигуры или другого геометрического объекта называется результат применения преобразования к исходному объекту. Образ может отличаться от исходного объекта по позиции, размерам или форме. Например, при повороте треугольника на 90 градусов, его образом будет новый треугольник, который ориентирован в другом направлении.
Прообразом точки, отрезка, фигуры или другого геометрического объекта называется исходный объект, который был преобразован в результате применения обратного преобразования к его образу. Прообраз позволяет определить, какой объект является исходным до преобразования. Например, при зеркальном отражении треугольника, его прообразом будет исходный треугольник, который отображается относительно оси симметрии.
Понятия образа и прообраза важны, так как они позволяют анализировать и сравнивать геометрические фигуры до и после преобразований. Они также помогают решать задачи на нахождение и определение свойств фигур, основываясь на их преобразованиях.
Образы и прообразы в геометрических аналогиях и метафорах
Понятие образа и прообраза, хорошо известное в геометрии, также находит применение в различных аналогиях и метафорах, позволяя нам лучше понять и описать различные явления и отношения.
Образ - это то, что получается в результате отображения или преобразования исходного объекта или явления. В геометрии, образом точки после преобразования может быть другая точка, линия или фигура. Аналогично, в контексте аналогий и метафор, образ может быть представлен в виде абстрактной концепции, слова, образа мыслей или ощущений.
Прообраз, с другой стороны, это исходный объект или явление, которое подвергается отображению или преобразованию. В геометрии, прообразом может быть начальная точка, линия или фигура, которые претерпевают преобразование и превращаются в образ. В аналогичных контекстах, прообраз может быть тем, что мы пытаемся описать или представить через образ.
Использование образов и прообразов в аналогиях и метафорах может помочь нам уяснить сложные и абстрактные понятия через геометрический язык и представления. Например, мы можем говорить о "отражении" человеческой натуры в искусстве или "поворотах" судьбы в жизни. Эти метафоры используют геометрические понятия образов и прообразов для создания более ярких и понятных описаний.
Таким образом, понимание образов и прообразов в геометрии помогает нам не только в изучении и практическом применении математических концепций, но и в расширении нашего лингвистического и когнитивного аппарата для описания мира вокруг нас.



