Полярная система координат – это система, которая используется для описания точек на плоскости с помощью угла и радиус-вектора. В отличие от привычной Декартовой системы координат, где точка определяется двумя числами (координатами x и y), в полярной системе координат точка описывается углом φ и радиусом r.
Ось радиуса в полярной системе координат направлена от начала координат (полюса) к точке, а угол φ измеряется от положительной полуоси x против часовой стрелки. Таким образом, каждая точка в плоскости имеет уникальные значения угла и радиуса, которые позволяют ее однозначно идентифицировать в полярной системе координат.
Полярная система координат находит широкое применение в различных областях науки и техники. Например, она используется для описания движения тел в физике, анализа колебаний и волн в математике, построения графиков функций и много других приложений.
Определение полярной системы координат
Первая координата r представляет собой расстояние от начала координат (полюса) до точки, а угол θ (тета) – это угол между положительным направлением оси абсцисс и лучом, соединяющим начало координат с точкой.
Таким образом, полярная система координат позволяет описывать положение точки в зависимости от угла и расстояния до нее от начала координат.
Преимущества использования полярной системы координат
Использование полярной системы координат обладает несколькими преимуществами:
| Преимущество | Описание |
|---|---|
| Простота и интуитивность | Полярная система координат позволяет более естественным образом описывать и визуализировать некоторые геометрические объекты, такие как окружности, спирали и радиальные симметричные фигуры. Она также более проста для понимания и использования в некоторых задачах, таких как описание движения по окружности или определение полярных координат объекта. |
| Удобство в навигации | Полярная система координат имеет особую значимость в навигации, особенно при указании направления и расстояния относительно определенной точки. Например, когда указывается направление судна относительно севера, часто используются полярные координаты. |
| Гибкость при работе с циклическими данными | Полярная система координат особенно полезна при работе с циклическими данными, такими как моменты времени или последовательности углов. Они позволяют более естественным образом отображать и анализировать периодические изменения данных. |
Использование полярной системы координат может быть полезным в ряде прикладных областей, включая физику, инженерию, географию, навигацию и многие другие. Она позволяет более удобным способом описывать и анализировать определенные геометрические и физические явления.
Применение полярной системы координат в различных областях
1. Математика: Полярные координаты широко используются в математике для представления графиков функций. Они часто используются для исследования кривых, спиралей, логарифмических спиралей и других геометрических фигур.
2. Физика: Полярная система координат часто используется в физике при изучении движения объектов или векторных полей. Она позволяет более удобно и понятно описывать направление и величину вектора в радиус-угловых координатах.
3. Инженерия: В инженерных расчетах и строительстве полярная система координат может быть использована для определения направления и расстояния между двумя точками. Она также может быть приложена в геодезии для измерения углов и расстояний на местности.
4. Радио и навигация: Полярная система координат часто используется в радио и навигационных системах, таких как радиолокация и GPS. Она позволяет определить точное положение объекта и его направление относительно определенной отправной точки.
5. Компьютерная графика: В компьютерной графике полярная система координат может быть использована для создания различных эффектов и анимаций, таких как вращение объектов или создание радиальных шаблонов и фигур.
6. Фотография и искусство: Полярная система координат может быть использована в фотографии и искусстве для создания любопытных перспективных эффектов или выравнивания объектов относительно определенных углов и линий.
Конвертация между полярной и прямоугольной системами координат
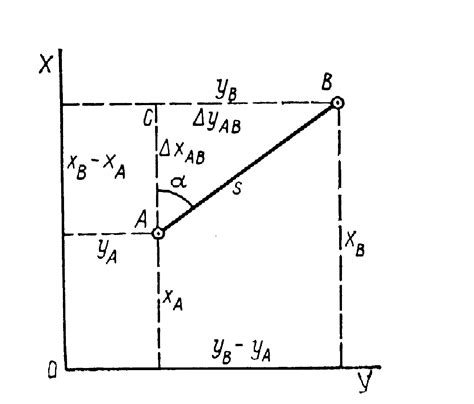
Для конвертации координат из полярной системы в прямоугольную систему можно использовать следующие формулы:
- Декартовы координаты (x, y) можно вычислить по полярным координатам (r, θ) с помощью формул:
- x = r * cos(θ)
- y = r * sin(θ)
Для конвертации координат из прямоугольной системы в полярную систему можно использовать следующие формулы:
- Полярные координаты (r, θ) можно вычислить по декартовым координатам (x, y) с помощью формул:
- r = sqrt(x^2 + y^2)
- θ = atan2(y, x)
Применение этих формул позволяет легко переходить от одной системы координат к другой и выполнять необходимые вычисления.



