Треугольники - это одна из самых основных геометрических фигур, изучаемая еще в школьной программе. Однако, когда дело доходит до определения и вычисления их площадей, возникают вопросы. Какие есть формулы для расчета площади треугольника? Как правильно решить задачу, если даны длины сторон или высота? В этой статье мы рассмотрим основные формулы и способы решения задач на вычисление площади треугольников.
Одной из самых известных формул для расчета площади треугольника является формула Герона. Она основана на полупериметре треугольника и длинах его сторон. Используя эту формулу, можно вычислить площадь треугольника, зная длины всех его сторон. Однако, есть и другие способы выразить площадь треугольника в формулах, например, через основание и высоту или через две стороны и угол между ними. Каждый из этих методов может быть использован в зависимости от данных, которые у вас есть.
Решение задач на вычисление площади треугольника не всегда является сложной задачей. Если известны длины всех сторон треугольника, то можно использовать формулу Герона. Если известны основание и высота, то можно воспользоваться формулой для прямоугольного треугольника. Если даны две стороны и угол между ними, то можно использовать формулу площади треугольника по формуле "половина произведения двух сторон на синус угла между ними". Важно правильно выбрать формулу в зависимости от данных, чтобы получить точный результат.
Что такое площади треугольников и зачем они нужны
Знание площадей треугольников может быть полезно в различных сферах жизни. Например, в строительстве и архитектуре оно позволяет точно рассчитывать количество материалов, необходимых для создания треугольных элементов конструкций.
В геодезии площади треугольников используются для определения площадей участков земли или перемеров, а также для построения геометрических карт.
Использование площадей треугольников в физике и инженерных науках позволяет решать разнообразные задачи, связанные с расчетом напряжений и деформаций в материалах.
Кроме того, площади треугольников имеют и образовательное значение. Изучение понятия площади и способов её измерения помогает развивать логическое мышление, аналитические и геометрические навыки.
В общем, знание площадей треугольников полезно в самых разных областях жизни и деятельности и помогает сделать точные и качественные расчеты и оценки.
Как выразить площадь треугольника в формуле
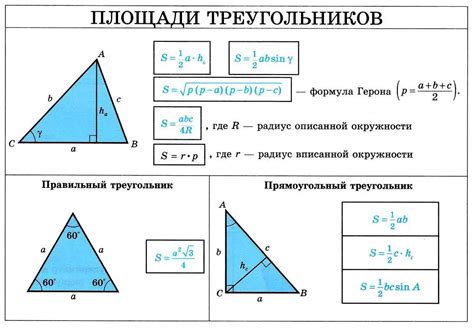
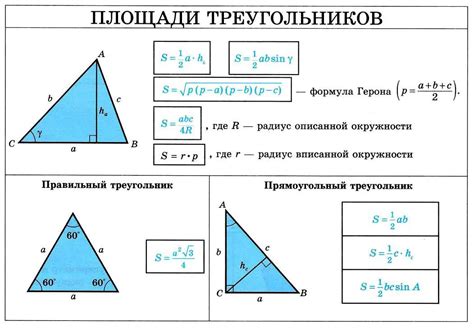
Формула Герона: Площадь треугольника можно выразить через длины его сторон, используя формулу Герона:
S = √(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, a, b, c - длины его сторон, а p - полупериметр треугольника, вычисляемый по формуле p = (a + b + c) / 2.
Формула полупериметра и радиуса описанной окружности: Площадь треугольника также можно выразить через полупериметр треугольника и радиус r окружности, описанной вокруг треугольника:
S = (a * b * c) / (4R),
где S - площадь треугольника, a, b, c - длины его сторон, и R - радиус описанной окружности.
Формула одной стороны и высоты: Если известна длина одной стороны треугольника и его высота, можно выразить площадь треугольника по формуле:
S = (a * h) / 2,
где S - площадь треугольника, a - длина одной стороны, и h - высота, опущенная на эту сторону.
Выберите соответствующую формулу в зависимости от известных данных о треугольнике, чтобы выразить его площадь в формуле. Зная значения всех необходимых величин, можно легко решить задачу на нахождение площади треугольника.
Площадь треугольника по формуле Герона

Пусть a, b и c - длины сторон треугольника, а p - полупериметр (p = (a + b + c) / 2). Тогда площадь треугольника можно вычислить по следующей формуле:
S = √(p(p - a)(p - b)(p - c)),
где S - площадь треугольника.
Чтобы вычислить площадь треугольника по формуле Герона, необходимо знать длины всех трех его сторон. Если их значения известны, то можно подставить их в формулу и выполнить необходимые вычисления.
Формула Герона особенно полезна, когда длины сторон треугольника известны, но его высота неизвестна или сложно найти. В этом случае она позволяет быстро и точно вычислить площадь треугольника без необходимости выполнять дополнительные действия.
Если известны только координаты вершин треугольника, то можно воспользоваться формулой Герона для вычисления его площади. Для этого необходимо сначала вычислить длины сторон треугольника, используя формулу расстояния между двумя точками в пространстве.
Площадь треугольника по формуле Герона является одним из основных способов вычисления площадей треугольников и широко применяется в геометрии и ее приложениях.
Что такое формула Герона и как ее использовать

Формула Герона выглядит следующим образом:
| S = √(p(p - a)(p - b)(p - c)) |
Где S – площадь треугольника, a, b, c – длины сторон треугольника, а p – полупериметр треугольника, который можно найти по формуле:
| p = (a + b + c) / 2 |
Для использования формулы Герона, необходимо знать длины всех трех сторон треугольника. Подставив эти значения в формулу, можно расчитать площадь треугольника.
Пример использования формулы Герона:
| a = 5, b = 7, c = 9 |
| p = (5 + 7 + 9) / 2 = 10 |
| S = √(10(10 - 5)(10 - 7)(10 - 9)) = √(10 * 5 * 3 * 1) = √150 = 12.247 |
Таким образом, площадь треугольника со сторонами 5, 7 и 9 равна примерно 12.247
Формула Герона является удобным инструментом для нахождения площади треугольников, особенно в случае, когда треугольник задан своими сторонами, а не высотой и основанием.
Шаги для вычисления площади треугольника по формуле Герона
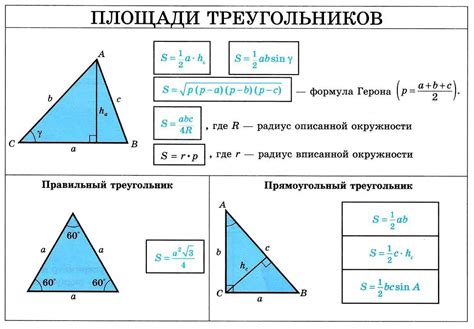
Шаг 2: Вычислите полупериметр треугольника, который рассчитывается по формуле:
p = (a + b + c) / 2
где p - полупериметр, a, b и c - длины сторон треугольника.
Шаг 3: Используя полученное значение полупериметра (p) и длины сторон треугольника (a, b и c), вычислите площадь треугольника по формуле Герона:
S = √(p * (p - a) * (p - b) * (p - c))
где S - площадь треугольника, p - полупериметр, a, b и c - длины сторон треугольника.
Шаг 4: Подставьте значения длин сторон треугольника в формулу Герона и выполните вычисления, чтобы найти площадь треугольника.
Шаг 5: Полученное значение является площадью треугольника. Убедитесь, что все единицы измерения согласованы и правильно округлите результат, если необходимо.
Площадь треугольника по формуле полувысоты и основания
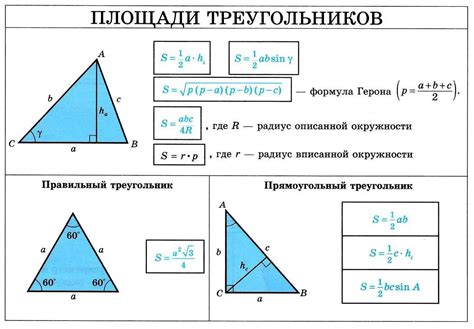
Для вычисления площади треугольника по формуле полувысоты и основания нужно знать длину основания треугольника (в большинстве случаев принимается за основание его наиболее длинная сторона) и длину проведенной к этому основанию полувысоты.
Формула для вычисления площади треугольника по формуле полувысоты и основания:
S = (1/2) * a * h
где S - площадь треугольника, a - длина основания, h - длина полувысоты, опущенной на это основание.
Применение этой формулы позволяет с легкостью вычислять площадь треугольника, когда известны его основание и полувысота. Такой метод особенно полезен, когда измерить все стороны и углы треугольника затруднительно или невозможно.
Обратите внимание, что в данной формуле полувысота проводится к основанию перпендикулярно, то есть создает прямой угол с основанием треугольника.
Примеры использования формулы полувысоты и основания
Рассмотрим несколько примеров применения данной формулы:
Пример 1:
Дан треугольник со сторонами a = 5, b = 7 и c = 9.
Вычислим площадь треугольника по формуле полувысоты и основания:
S = (1/2) * b * h,
где h - полувысота треугольника.
Сначала найдем полупериметр треугольника:
p = (a + b + c) / 2 = (5 + 7 + 9) / 2 = 21 / 2 = 10.5.
Затем найдем полувысоту треугольника, используя формулу:
- h = 2 * sqrt(p * (p - a) * (p - b) * (p - c)) / a = 2 * sqrt(10.5 * (10.5 - 5) * (10.5 - 7) * (10.5 - 9)) / 5 = 2 * sqrt(10.5 * 5.5 * 3.5 * 1.5) / 5 ≈ 6.02.
Теперь, подставив значения в формулу площади, получим:
- S = (1/2) * b * h = (1/2) * 7 * 6.02 = 3.51.
Таким образом, площадь треугольника равна 3.51.
Пример 2:
Дан треугольник со сторонами a = 8, b = 6 и c = 10.
Вычислим площадь треугольника по формуле полувысоты и основания:
S = (1/2) * b * h,
где h - полувысота треугольника.
Сначала найдем полупериметр треугольника:
p = (a + b + c) / 2 = (8 + 6 + 10) / 2 = 24 / 2 = 12.
Затем найдем полувысоту треугольника, используя формулу:
- h = 2 * sqrt(p * (p - a) * (p - b) * (p - c)) / a = 2 * sqrt(12 * (12 - 8) * (12 - 6) * (12 - 10)) / 8 = 2 * sqrt(12 * 4 * 6 * 2) / 8 ≈ 6.
Теперь, подставив значения в формулу площади, получим:
- S = (1/2) * b * h = (1/2) * 6 * 6 = 18.
Таким образом, площадь треугольника равна 18.
Пример 3:
Дан треугольник со сторонами a = 12, b = 16 и c = 20.
Вычислим площадь треугольника по формуле полувысоты и основания:
S = (1/2) * b * h,
где h - полувысота треугольника.
Сначала найдем полупериметр треугольника:
p = (a + b + c) / 2 = (12 + 16 + 20) / 2 = 48 / 2 = 24.
Затем найдем полувысоту треугольника, используя формулу:
- h = 2 * sqrt(p * (p - a) * (p - b) * (p - c)) / a = 2 * sqrt(24 * (24 - 12) * (24 - 16) * (24 - 20)) / 12 = 2 * sqrt(24 * 12 * 8 * 4) / 12 ≈ 15.49.
Теперь, подставив значения в формулу площади, получим:
- S = (1/2) * b * h = (1/2) * 16 * 15.49 = 123.92.
Таким образом, площадь треугольника равна 123.92.
Таким образом, формула полувысоты и основания позволяет быстро и точно вычислить площадь треугольника при наличии информации о его основании и полувысоте.
Как решить треугольник, если даны только полувысота и основание

Решение треугольника можно провести, даже если известны только полувысота и основание. Для этого применим формулу для вычисления площади треугольника, которая основана на полувысоте и основании.
Для начала вспомним формулу для вычисления площади треугольника по полувысоте и основанию:
S = (h * b) / 2,
где:
- S - площадь треугольника,
- h - полувысота треугольника,
- b - основание треугольника.
Чтобы найти площадь треугольника, имея только полувысоту и основание, нужно умножить полувысоту на основание и разделить полученное значение на 2.
Применяя эту формулу, можно решить треугольник и вычислить его площадь, даже если изначально известны только полувысота и основание, без дополнительных данных о сторонах.
Если вам известны значения полувысоты и основания треугольника, вы можете использовать эту формулу для быстрого и точного вычисления площади треугольника.



