Математика всегда нам предлагает интересные и необычные задачи. Одна из таких загадок связана с площадью многоугольника, описанного около окружности. Какую площадь он занимает? Эта вопрос может показаться довольно сложным, но на самом деле он имеет простое и удивительное решение.
Давайте вспомним, что такое описанная около окружности фигура. Это многоугольник, вершины которого касаются окружности, а стороны проходят через центр этой окружности. Таким образом, каждый угол многоугольника будет равен половине центрального угла окружности, созданного двумя пересекающимися сторонами.
Итак, как вычислить площадь такого многоугольника? Воспользуемся формулой площади треугольника, которая равна половине произведения длин стороны и высоты, проведенной к этой стороне. Затем умножим полученную площадь на количество треугольников, образующих многоугольник, и получим ответ.
Загадка: Решение формулы площади описанного около окружности многоугольника
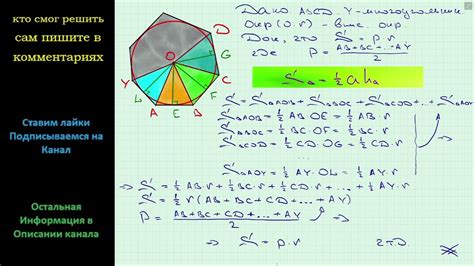
Для решения данной загадки необходимо знать формулу площади описанного около окружности многоугольника. Она выглядит следующим образом:
S = R² * n * sin(360° / n)
Где:
- S - площадь многоугольника;
- R - радиус описанной окружности;
- n - количество сторон многоугольника.
Эта формула позволяет вычислить площадь многоугольника, который описывает окружность с заданным радиусом.
Для расчета площади необходимо знать радиус описанной окружности и количество сторон многоугольника. После подстановки этих значений в формулу можно получить искомую площадь многоугольника.
Надеемся, что данная информация поможет вам разгадать загадку и найти площадь многоугольника.
Многоугольник описанный около окружности: особенности и свойства
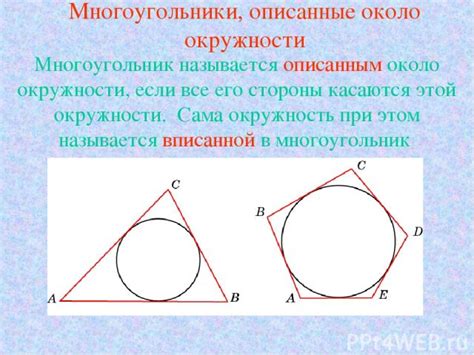
Важной характеристикой многоугольника описанного около окружности является его радиус. Радиус окружности, описанной вокруг многоугольника, будет равен радиусу окружности, если все его стороны и углы равны. В противном случае, радиус окружности будет различаться для каждого многоугольника.
Помимо радиуса, ещё одной важной характеристикой многоугольника описанного около окружности является его площадь. Площадь многоугольника описанного около окружности зависит от количества сторон этого многоугольника и длины каждой стороны.
Загадка: "Чему равна площадь многоугольника описанного около окружности?" оставляет ответ открытым, так как точный ответ будет зависеть от конкретных размеров и характеристик этого многоугольника.



