Площадь квадрата 48 см2 — вычисляем его периметр

Квадрат - это одна из самых простых и популярных геометрических фигур. У квадрата все стороны равны друг другу, а углы - прямые. Одно из основных свойств квадрата - его площадь. Если известна площадь квадрата, можно вычислить длину его стороны, а также периметр.

Представим, что площадь квадрата составляет 48 см². Для того чтобы найти периметр, нам нужно узнать длину его стороны. Площадь квадрата вычисляется по формуле: S = a², где S - площадь, а a - длина стороны.

Исходя из этой формулы, мы можем найти длину стороны квадрата, воспользовавшись корнем из площади. Так как площадь квадрата равна 48 см², то сторона будет равна корню из 48: a = √48 = 6√2 см.

Теперь, когда мы знаем длину стороны квадрата, можем вычислить его периметр. Периметр квадрата равен сумме всех его сторон, то есть 4a.

Как вычислить периметр квадрата с площадью 48 см2?

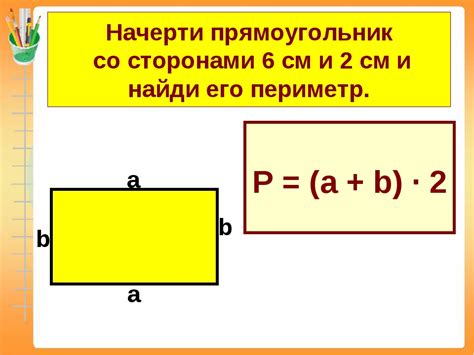
Площадь квадрата вычисляется по формуле: S = a2, где a - длина стороны квадрата. Выразим длину стороны квадрата из формулы площади: a = √S. В нашем случае S = 48 см2. Подставим значение площади в формулу и вычислим длину стороны: a = √48 = 6.93 см (округлим до сотых).

Теперь, когда мы знаем длину стороны квадрата, можем вычислить его периметр по формуле P = 4 * a: P = 4 * 6.93 = 27.72 см (округлим до сотых).

Таким образом, периметр квадрата с площадью 48 см2 равен 27.72 см.

Формула для вычисления периметра квадрата

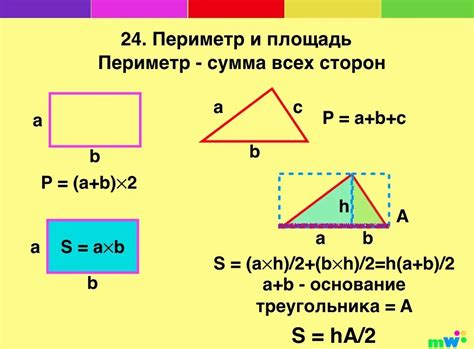
Для нахождения длины стороны квадрата по известной площади необходимо использовать следующую формулу:

S = a^2

где S – площадь квадрата, а a – длина стороны.

Для нахождения периметра квадрата, имея длину его стороны, следует использовать формулу:

P = 4a

где P – периметр квадрата.

В данном случае, если площадь квадрата равна 48 см², мы можем найти длину его стороны следующим образом:

48 = a^2

Для нахождения длины стороны a необходимо извлечь квадратный корень из обоих частей уравнения:

a = √48

После нахождения длины стороны квадрата, мы можем посчитать его периметр по формуле:

P = 4 * √48

Таким образом, периметр квадрата с площадью 48 см² равен 4 умножить на корень из 48. После вычислений, периметр можно округлить до нужного числа знаков после запятой.

Известная площадь квадрата и периметр

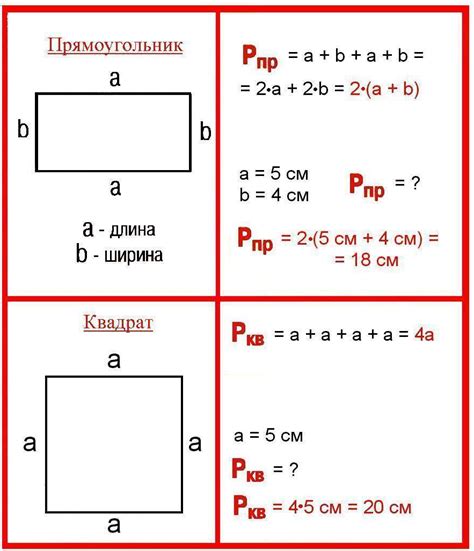
Зная площадь квадрата, можно найти его периметр, используя несколько простых математических формул. Площадь квадрата вычисляется как произведение длины одной из его сторон на эту же длину. Таким образом, если площадь квадрата равна 48 см2, то мы можем найти длину одной его стороны.

Для этого нужно найти квадратный корень из площади. В данном случае, квадратный корень из 48 равен примерно 6,93. Это значит, что длина стороны квадрата приблизительно равна 6,93 см.

Чтобы найти периметр квадрата, нужно умножить длину его стороны на 4, так как все стороны квадрата равны. В нашем случае, периметр квадрата будет равен приблизительно 27,72 см.

Итак, если известна площадь квадрата и нужно найти его периметр, необходимо выполнить следующие шаги:

1. Найти квадратный корень из площади, чтобы найти длину одной стороны квадрата.
2. Умножить длину стороны на 4, чтобы найти периметр квадрата.

Теперь мы можем использовать эти шаги, чтобы найти периметр квадрата с площадью 48 см2 и любой другой известной площадью.

Пример вычисления периметра квадрата с площадью 48 см²

Для вычисления периметра квадрата с заданной площадью 48 см² необходимо воспользоваться формулой, связывающей периметр и площадь квадрата.

Площадь квадрата вычисляется по формуле:

Площадь = сторона * сторона

Дано: площадь = 48 см²

Необходимо найти значение стороны квадрата и вычислить его периметр.

Решение:

1. Подставим известное значение площади в формулу площади квадрата:

48 см² = сторона * сторона

2. Решим полученное уравнение относительно стороны:

сторона = √48 см

3. Вычислим значение стороны:

сторона = √16 * √3 см = 4√3 см

4. Вычислим периметр квадрата, зная значение стороны:

Периметр = 4 * сторона = 4 * 4√3 см = 16√3 см

Таким образом, периметр квадрата с площадью 48 см² равен 16√3 см.