Сорок четыре избирателя

Однако, когда подводят итоги голосования, оказывается, что принято было 30 решений в пользу A и 14 решений в пользу B. Как такое возможно?
Дело в том, что каждый избиратель мог голосовать за оба предложения или воздержаться от голосования. И если из 26 человек, которые проголосовали за A, 4 также проголосовали за B, а 2 воздержались от голосования, то общее число решений в пользу A составляет 30 (26 + 4), а число решений в пользу B - 14 (18 - 4).
Таким образом, эта ситуация показывает, что количество голосов за каждое предложение не всегда отражает реальное мнение избирателей, так как люди могут голосовать за несколько предложений или воздержаться от голосования.
| Предложение | Количество голосов |
|---|---|
| A | 30 |
| B | 14 |
Парадокс Бертрана
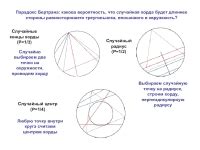
Идею парадокса впервые высказал французский математик Жозеф Бертран в 1889 году. Этот парадокс связан с размещением окружностей внутри треугольника.
Существует несколько способов размещения окружностей внутри треугольника: около вписанной окружности, описанной окружности и окружности минимального радиуса.
Парадокс Бертрана заключается в том, что необходимо указать, какое конкретное размещение окружностей имелось в виду, чтобы получить однозначный ответ.
Если вопрос сформулирован ясно и точно, то можно утверждать, что в треугольнике всегда можно найти окружности, которые удовлетворяют указанным условиям. Однако, если вопрос сформулирован с неопределенностью, то можно привести примеры, когда ответы будут различными.
Парадокс Бертрана демонстрирует важность ясной и точной формулировки задачи в математике, а также то, что одна и та же задача может иметь разные решения в зависимости от формулировки. Этот парадокс подчеркивает ограничения математических моделей и напоминает, что математика не всегда ведет нас к истине.
Парадокс Монти Холла
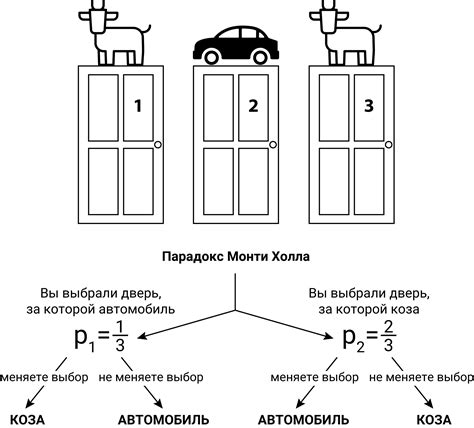
Парадокс заключается в следующей ситуации: у вас есть три закрытых двери, за одной из которых находится автомобиль, а за двумя остальными - козы. Вы выбираете одну из дверей, например, номер 1. После этого ведущий шоу, зная, что находится за каждой дверью, открывает одну из оставшихся дверей, за которой находится коза (например, дверь номер 3).
Затем ведущий предлагает вам пересмотреть свой выбор и выбрать другую из оставшихся закрытых дверей - дверь номер 2. И вот здесь происходит парадокс: ведущий утверждает, что вероятность выигрыша автомобиля у вас увеличивается, если вы измените свой выбор и выберете другую дверь.
Хотя на первый взгляд может показаться, что вероятность выигрыша должна быть равной 1/2 независимо от выбора, на самом деле это не так. Успех выбора новой двери возрастает до 2/3, а шансы на выигрыш при сохранении первоначального выбора - снижаются до 1/3.
Парадокс Монти Холла обычно объясняется с помощью условной вероятности. Когда вы выбираете дверь вначале, вероятность выбрать дверь с автомобилем составляет 1/3. При открытии ведущим одной из дверей с козой, шансы перевешивают на оставшуюся закрытую дверь. Вероятность выбрать новую дверь с автомобилем становится 2/3. Поэтому вы чаще выигрываете, если меняете свой выбор.
| Выбрал | Автомобиль | Коза | Коза |
|---|---|---|---|
| 1 | 2 | 3 | |
| 2 | 1 | 3 | |
| 3 | 1 | 2 |
Таблица выше иллюстрирует возможные расположения автомобиля и коз за дверьми при разных выборах игрока. Из нее видно, что при изменении выбора с первой двери на вторую, вы всегда выигрываете автомобиль.
Парадокс Монти Холла продолжает вызывать споры и дебаты среди математиков и логиков. Он демонстрирует, что интуитивные ожидания и логическое рассуждение могут противоречить друг другу. Он также показывает, что математика иногда может привести нас к неожиданным и контринтуитивным результатам, отличающимся от наших интуитивных ожиданий.
Задача про двух карликов

Однажды два карлика, Али и Боб, сражались в поединке. Каждый из них был вооружен мечом и щитом, и они оказались в необычной ситуации. Щиты карликов были сделаны из особого материала, который мог быть пронзен только мечом другого карлика. Они понимали, что в этой ситуации нельзя достичь победы, и решили взять друг у друга по одному удару и потом остановиться.
Первым ударил Али по щиту Боба, и его меч пронзил его щит. Затем Боб ударил по щиту Али, и его меч тоже пронзил его щит.
Теперь у карликов возник вопрос: кто победил? Они обсуждали эту задачу и не могли прийти к единому мнению. Некоторые считали, что побеждает тот, кто первым пронзил щит, то есть Али, в то время как другие считали, что побеждает тот, чей щит был пронзен последним, то есть Боб.
Возникает парадокс: оба карлика одновременно и победили, и проиграли. Данная ситуация показывает, что математика не всегда приводит нас к истине и может порождать парадоксы. В этой задаче есть логическая несостоятельность, которая показывает наличие противоречий в математических рассуждениях.
Таким образом, задача про двух карликов демонстрирует ограничения математического аппарата на пути к полной истины. Парадоксы и софизмы в математике служат напоминанием о том, что нельзя полностью полагаться на формулы и модели, и всегда нужно проводить анализ и критические рассуждения, чтобы достигнуть истинного понимания.
Парадокс Рассела
Парадокс Рассела звучит следующим образом: "Рассмотрим множество всех множеств, которые не содержат самих себя в качестве элементов. Вопрос: будет ли это множество содержать само себя?". Если ответ "да", то оно не удовлетворяет определению, поскольку содержит само себя в качестве элемента. Если ответ "нет", то оно должно быть включено в множество, так как все множества, не содержащие себя в качестве элементов, должны быть включены в это множество. В любом случае возникает противоречие.
| Множество | Содержит само себя |
|---|---|
| 1. Множество всех книг в библиотеке | Нет |
| 2. Множество всех кресел в комнате | Нет |
| 3. Множество всех множеств, которые не содержат себя в качестве элементов | ??? |
Парадокс Рассела подчеркивает сложность с абсолютной логикой и всегда вызывает размышления у математиков и философов. Он показывает, что некоторые вопросы и определения могут быть саморазрушающимися или вводящими в заблуждение.
Парадокс Рассела является примером того, как математика может не всегда вести нас к истине и показывает, что необходимо быть осторожными с саморефлексией и неоднозначностью в определениях и аксиомах. Он продолжает быть одним из основных камней преткновения в изучении логики и основ математики.
Неплохая трактовка

Парадоксы и софизмы – это явления, которые свидетельствуют о том, что математика не всегда ведет нас к истине. Они могут возникать из-за неправильного применения математических методов или из-за недостаточного понимания основных понятий и правил.
Одной из возможных трактовок этого явления является то, что математика – это искусство, а не только наука. В отличие от других искусств, математика стремится к абсолютной истине и логической последовательности.
Однако, как и в искусстве, в математике есть место для творчества и неопределенности. Иногда решение математической проблемы может иметь несколько вариантов, и выбор между ними может быть субъективным.
Также, в математике часто используются абстрактные понятия и модели, которые не всегда полностью отражают реальность. Например, в геометрии мы представляем прямую линию или окружность как идеальные объекты, хотя на самом деле они не могут быть достигнуты в реальном мире.
Цепочка отрицаний

Представим, что у нас есть три пропозиции: пропозиция А, пропозиция В и пропозиция С. Каждая из них может быть истинной (правдивой) или ложной (неправдивой).
Если мы предположим, что А истинно, то, в соответствии с первым утверждением, В должно быть ложно. Но тогда, в соответствии со вторым утверждением, С должно быть ложно. Однако, это приводит к противоречию с третьим утверждением, которое заявляет, что А ложно. Таким образом, наше предположение было неверным, и А на самом деле ложно.
Теперь мы можем предположить, что А ложно. Значит, в соответствии с третьим утверждением, С истинно. В свою очередь, в соответствии со вторым утверждением, В должно быть ложно. Однако, это противоречит первому утверждению, которое говорит, что А ложно. Таким образом, наше предположение было неверным, и А на самом деле истинно.
Мы можем сделать аналогичные рассуждения и для В и С. В конечном итоге мы приходим к противоречивым результатам независимо от начального предположения об истинности или ложности каждой из пропозиций.
Цепочка отрицаний показывает, что логические операции отрицания могут создавать парадоксы, где истинность и ложность пропозиций путаницы и противоречий. Эти парадоксы подчеркивают ограничения логики и осложняют установление истинности в математических рассуждениях.



