Тетраэдр и правильная треугольная пирамида – две геометрические фигуры, которые, на первый взгляд, могут показаться схожими. Однако, при более детальном рассмотрении, можно увидеть некоторые важные различия между ними.
Во-первых, основание тетраэдра и правильной треугольной пирамиды отличается формой. У тетраэдра основание является треугольником, состоящим из трех равных сторон. В то же время, у правильной треугольной пирамиды основание также является треугольником, но все его стороны и углы равны.
Во-вторых, количество граней у тетраэдра и правильной треугольной пирамиды также различается. Тетраэдр имеет четыре грани, в то время как у правильной треугольной пирамиды их количество может быть любым, но всегда больше четырех.
Наконец, важным отличием между этими двумя фигурами является количество вершин. У тетраэдра четыре вершины, которые образуют четыре треугольника. В правильной треугольной пирамиде количество вершин зависит от количества граней, но всегда больше четырех.
Таким образом, тетраэдр и правильная треугольная пирамида имеют несколько важных отличий. Они различаются формой основания, количеством граней и вершин. Понимание этих различий позволяет лучше понять их свойства и применение в различных областях геометрии и математики.
Структура тетраэдра и правильной треугольной пирамиды
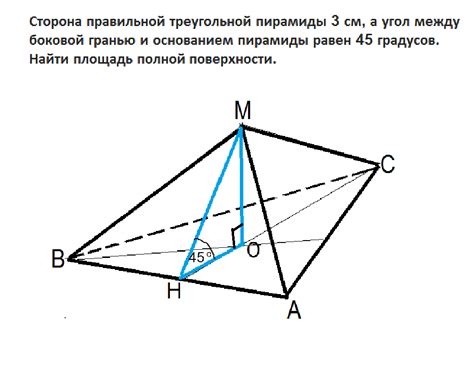
Тетраэдр - это многогранник, состоящий из четырех треугольных граней. Он имеет четыре вершины и шесть ребер. Такая структура делает тетраэдр стабильным и устойчивым к деформациям. Тетраэдр обладает симметрией, то есть каждая его грань и каждое его ребро имеют аналогичные соседние грани и ребра.
Правильная треугольная пирамида - это многогранник, состоящий из четырех треугольных граней и одной основной треугольной грани. У пирамиды также четыре вершины и шесть ребер. Однако, основной отличительной особенностью правильной треугольной пирамиды является равномерное распределение углов и сторон между всеми гранями и ребрами.
Оба многогранника имеют свои применения в разных областях. Тетраэдр широко используется в геометрии и физике, например, в численных методах и в моделировании структуры молекул. Правильная треугольная пирамида встречается в архитектуре и визуальных искусствах, так как ее симметрия и гармоничные формы являются привлекательными для глаза.
Количество граней, рёбер и вершин
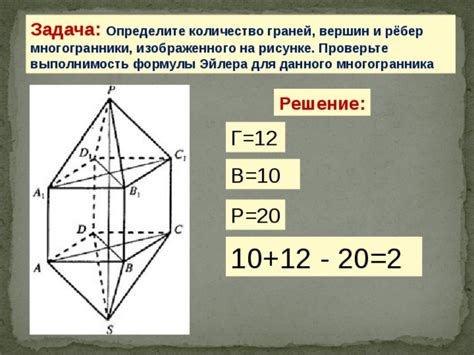
Тетраэдр, также известный как треугольная пирамида, имеет 4 грани, состоящие из треугольников, 6 рёбер и 4 вершины. Грани тетраэдра являются треугольными, а каждое ребро соединяет две из этих граней. Вершины тетраэдра являются точками, где пересекаются три его грани.
С другой стороны, правильная треугольная пирамида имеет 5 граней, составленных из треугольников, 9 рёбер и 4 вершины. Грани пирамиды также являются треугольными, однако они отличаются от граней тетраэдра по своему числу. Каждое ребро пирамиды соединяет две из её граней, а вершины пирамиды - точки пересечения трёх граней.
Таким образом, количество граней, рёбер и вершин различается для тетраэдра и правильной треугольной пирамиды, что отличает эти две фигуры друг от друга.
Форма и размеры фигур

Тетраэдр является многогранником, состоящим из четырех треугольных граней. У каждой из этих граней есть три стороны и три угла. Все грани встречаются в вершине, образуя три равносторонних треугольника. Тетраэдр имеет четыре вершины, шесть ребер и четыре грани.
Правильная треугольная пирамида, как и тетраэдр, имеет четыре грани. Однако, каждая из этих граней - равносторонний треугольник, у которого все стороны и углы равны между собой. Основание пирамиды также является треугольником. Такая пирамида имеет четыре вершины, шесть ребер и четыре грани.
Несмотря на то, что оба тела имеют четыре грани, их формы и размеры существенно отличаются. Тетраэдр выглядит как пирамида с треугольным основанием и треугольными боковыми гранями, тогда как правильная треугольная пирамида имеет четыре равносторонние треугольные грани.
Ориентация граней и ребер
Тетраэдр и правильная треугольная пирамида имеют различную ориентацию граней и ребер.
В тетраэдре каждая грань является треугольником, а у пирамиды каждая грань может быть любым многоугольником.
Тетраэдр имеет 4 грани и 6 ребер. У него также 4 вершины. Все грани тетраэдра имеют одинаковую ориентацию, то есть нормали граней направлены в одну и ту же сторону.
Правильная треугольная пирамида имеет 4 грани и 6 ребер, также как и тетраэдр. Однако у пирамиды ориентация граней может быть различной. Нормали граней пирамиды направлены в разные стороны.
У обоих тел нет параллельных ребер или граней.
Таким образом, ориентация граней и ребер является основным отличием между тетраэдром и правильной треугольной пирамидой.
Как обозначать имена вершин и ребер
В тетраэдре и правильной треугольной пирамиде вершины обозначаются заглавными буквами, например, А, В, С и D. Для каждой вершины тетраэдра существует соответствующая вершина на плоскости основания пирамиды, что и обозначено этими буквами.
Ребра тетраэдра и пирамиды обозначаются парами вершин, между которыми они проходят. Таким образом, ребро, соединяющее вершины А и В, обозначается AB.
Важно отметить, что порядок вершин при обозначении ребер имеет значение. Например, ребра AB и BA - это разные ребра, так как они соединяют вершины в разном порядке.
Использование обозначений вершин и ребер позволяет четко определить геометрическую структуру и связи в тетраэдре и правильной треугольной пирамиде.
Взаимное расположение граней и ребер
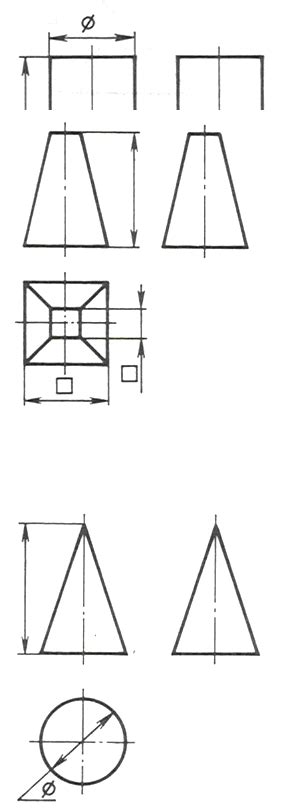
Правильная треугольная пирамида, в свою очередь, также имеет четыре грани, причем три из этих граней являются треугольниками, а одна - основанием пирамиды. Грани пирамиды не являются смежными между собой. Ребра пирамиды имеют разную длину, в отличие от тетраэдра.
Таким образом, взаимное расположение граней и ребер у тетраэдра отличается от правильной треугольной пирамиды. Тетраэдр является более симметричной фигурой, в которой грани и ребра тесно связаны друг с другом, в то время как пирамида имеет основание и грани, которые не смежны друг с другом.
Возможность разложения на составляющие треугольники
Технически, на первый взгляд, тетраэдр и правильная треугольная пирамида могут показаться похожими, ведь оба тела состоят из треугольных граней. Однако основное отличие между ними заключается в возможности разложения на составляющие треугольники.
Тетраэдр состоит из четырех треугольных граней, каждая из которых является частью его структуры. Это значит, что невозможно разложить тетраэдр на меньшие треугольники без изменения его формы.
В отличие от тетраэдра, правильная треугольная пирамида имеет треугольную основу и треугольные боковые грани. Такая пирамида может быть разложена на треугольные пластины, которые соединяются вокруг ее вершины. Это позволяет нам легко визуализировать и представить себе ее структуру.
Таким образом, главное отличие между тетраэдром и правильной треугольной пирамидой заключается в возможности разложения на составляющие треугольники. Это дает нам возможность лучше понять и представить структуру и форму данных тел.
Применение тетраэдра и правильной треугольной пирамиды
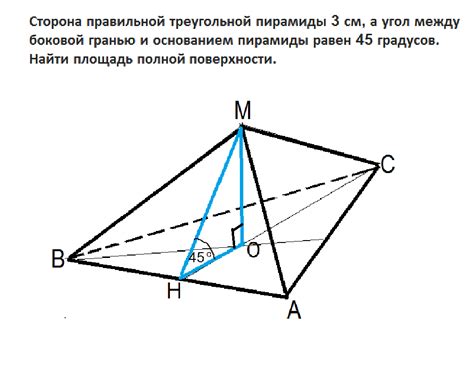
Тетраэдр является пространственной фигурой, состоящей из четырех треугольных граней. Его основные применения включают моделирование молекулярных структур в химии и биологии, конечно-элементный анализ в инженерии и архитектурном проектировании.
Тетраэдр используется для создания ячеистых структур в материалах, таких как пены и пористые материалы, которые обеспечивают свойства, такие как легкость, прочность и теплоизоляция. Он также играет важную роль в различных математических моделях и компьютерной графике.
С другой стороны, правильная треугольная пирамида - это фигура, у которой основание представляет собой равносторонний треугольник, а остальные грани - треугольники. Правильные треугольные пирамиды широко используются в геометрии при изучении свойств треугольников и объемных фигур.
Также элементы пирамидальной формы в архитектуре и скульптуре часто создаются с помощью правильных треугольных пирамид. Они придают конструкциям особую эстетическую привлекательность и стабильность.
В общем, тетраэдр и правильная треугольная пирамида играют важную роль в различных научных исследованиях, инженерных применениях и художественных проектах, продемонстрировав свою уникальность и функциональность.



