Машина поста и машина Тьюринга - два важных понятия в области вычислимости и теории автоматов. Эти понятия представляют собой модели вычислительных машин, которые помогают нам понять, что можно и что нельзя вычислить.
Машина поста, названная в честь американского математика Эмила Поста, является абстрактной вычислительной моделью, которая оперирует с понятием "программа". Она состоит из конечного числа состояний и принимает на вход некоторую строку символов (входные данные). Машина поста читает символы из этой строки и в зависимости от текущего состояния и считанного символа переходит в другое состояние, записывая на выход другой символ. Таким образом, машина поста осуществляет некоторое определенное вычисление над входными данными.
В отличие от машины поста, машина Тьюринга, предложенная английским математиком Аланом Тьюрингом, является более мощной вычислительной моделью. Она также состоит из конечного числа состояний, но вместо чтения строки символов, машина Тьюринга имеет неограниченную ленту, на которой записаны символы. Машина Тьюринга может перемещаться по этой ленте, изменять значения символов и переходить в другие состояния в зависимости от текущего состояния и символа, который она увидела.
Таким образом, основное отличие машины поста от машины Тьюринга заключается в их вычислительных возможностях. Машина Тьюринга является универсальной вычислительной машиной, что означает, что с ее помощью можно вычислить все, что можно вычислить на машинах поста, а также выполнить множество других вычислений, которые на машинах поста невозможны.
Машина поста и машина тьюринга: основные принципы идеи механического вычисления

Машина поста и машина тьюринга представляют собой две модели универсальных механических вычислительных устройств, разработанных в середине XX века математиками Эмилем Постом и Аланом Тьюрингом соответственно.
Обе машины построены на основе идеи создания абстрактной вычислительной машины, способной выполнять различные операции над символами в соответствии с заранее заданными правилами. Хотя их конструкция и функциональность отличаются, основные принципы их работы сходны.
Машина поста представляет собой последовательность шагов, которые выполняются над некоторым входным словом. Входное слово может быть представлено в виде бесконечной последовательности единиц и нулей, которые хранятся в бесконечной памяти машины. Каждый шаг машины поста состояит в перемещении машины влево или вправо, изменении символа в текущей ячейке и переходе к следующему шагу в соответствии с некоторыми заданными правилами. Работа машины поста продолжается до тех пор, пока не будет достигнута конечная ячейка или выполнено заданное условие остановки.
Машина тьюринга также использует понятие бесконечной памяти и заданных правил, но отличается от машины поста своей конструкцией и функцией. Она состоит из бесконечной ленты, разбитой на ячейки, которые могут содержать символы. Машина тьюринга имеет головку, которая может считывать и записывать символы на ленте, а также перемещать ленту влево или вправо. Основная идея машины тьюринга состоит в том, что она может выполнить любое вычисление, используя только ограниченное число операций и правил, которые предопределены перед началом выполнения. Работа машины тьюринга продолжается до достижения состояния остановки или выполнения заданного условия.
Обе машины являются абстрактными моделями, которые позволяют математикам и информатикам изучать основные принципы механического вычисления и разрабатывать новые алгоритмы и программы. Благодаря этим моделям была создана теория вычислимости, которая легла в основу современной информатики и компьютерных наук.
Машина поста: устройство и примеры применения
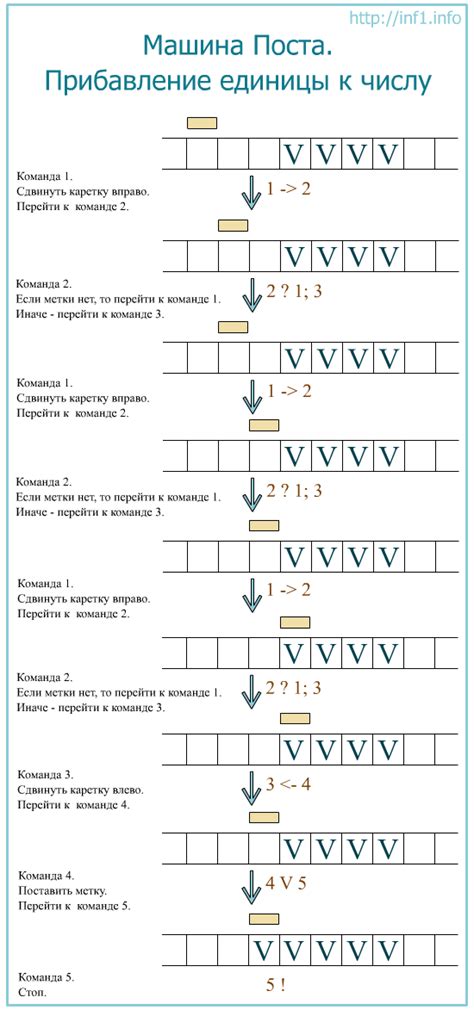
Устройство машины поста состоит из алфавита, правил перехода и управляющего устройства. Алфавит представляет собой ограниченный набор символов, которые могут быть использованы на ленте. Правила перехода определяют, какой символ заменить другим символом в определенной позиции, а управляющее устройство определяет порядок выполнения действий.
Машина поста может использоваться для решения различных задач, включая символьные вычисления, формальные грамматики, алгоритмы искусственного интеллекта и теорию языков. Она также может быть использована для исследования различных аспектов вычислений и исследования теоретических моделей вычислений.
Примером применения машины поста может быть решение задачи проверки грамматики. Машина поста может быть настроена на определенную грамматику и использоваться для проверки, принадлежит ли строка этой грамматике или нет. Она также может быть использована для решения задачи поиска и подстановки символов в строке или для генерации строк, удовлетворяющих определенным правилам.
Машина Тьюринга: инновационный подход и практические применения
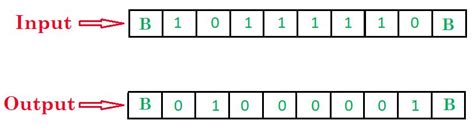
Инновационность подхода машины Тьюринга заключается в ее простоте и универсальности. Она стала основой для развития теории алгоритмов и теории вычислимости, а также является фундаментом для понимания основных принципов работы современных компьютеров и программного обеспечения.
Машина Тьюринга имеет огромное практическое значение в области информатики и вычислительной техники. Ее концепция активно применяется при разработке алгоритмов и программного обеспечения, в теории сложности вычислений, в криптографии, в искусственном интеллекте и многих других областях. Благодаря машине Тьюринга, компьютерные ученые и инженеры получили инструмент, с помощью которого можно формализовать и оптимизировать процессы и алгоритмы вычислений.
Следует отметить, что машина Тьюринга не ограничивается только вычислениями и разработкой алгоритмов. Она также находит свое применение в теории языков и формальных грамматиках, в численных методах, в теории игр и во многих других областях, где требуется формализация и моделирование процессов.



