Векторы являются одним из основных понятий в геометрии, и они играют важную роль в решении различных задач. Направление вектора - это одно из его ключевых свойств. Очень важно понимать, от чего зависит направление вектора и как его определить.
Направление вектора определяется с помощью двух точек: его начальной точки и конечной точки. Обозначается вектор стрелкой, указывающей от начальной точки к конечной точке. Зависит направление вектора от отношения между этими двумя точками.
Отношение между начальной и конечной точкой вектора определяется между другими векторами или особенностями пространства, в котором он находится. Вектор может быть направлен вдоль осей координат, от одной точки к другой, в направлении определенного угла относительно другого вектора или оси.
Направление вектора в геометрии также может иметь большую значимость при решении задач. Вектора могут быть сонаправлены, противоположно направлены или перпендикулярны друг другу. Понимание этой концепции помогает в решении задач на координатной плоскости, работе с фигурами и расчете углов между векторами.
Физическая природа векторов
Векторы отражают физические величины, которые имеют не только величину, но и направление. Физическая природа вектора определяется его геометрическим представлением и математическими операциями, которые можно выполнить с векторами.
Векторы могут представлять силы, скорости, ускорения и другие физические величины. Например, векторная сила указывает направление и силу, с которой действует тело на другое тело. Векторная скорость показывает направление и скорость движения тела.
Физическая природа векторов позволяет использовать их для анализа различных физических явлений. Векторные операции, такие как сложение, вычитание и умножение вектора на скаляр, позволяют моделировать и предсказывать различные физические процессы.
Кроме того, векторы используются для описания геометрических объектов в трехмерном пространстве, таких как отрезки, лучи и плоскости. Векторное представление обеспечивает более точное и компактное описание этих объектов, позволяя более удобно выполнять операции над ними.
Таким образом, физическая природа векторов является фундаментальной и важной для понимания многих физических явлений и их математического моделирования. Понимание этой природы позволяет глубже вникнуть в суть векторных величин и использовать их эффективно в различных областях науки и техники.
Свойства векторов в геометрии
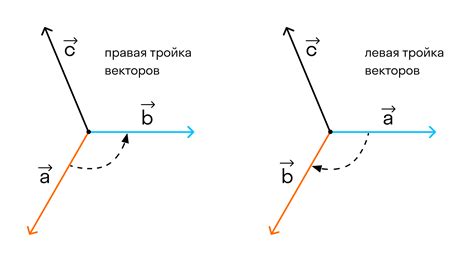
Векторы в геометрии обладают рядом важных свойств, которые определяют их направление и масштаб. Некоторые из этих свойств включают:
- Длина (модуль) - это свойство показывает, насколько "длинным" или "коротким" является вектор. Определение длины вектора основано на понятии расстояния между его началом и концом.
- Направление - это свойство указывает, в каком направлении движется вектор. Оно обычно определяется относительно осей координат или других точек в пространстве.
- Сложение - векторы можно складывать и получать новый вектор, который представляет комбинацию их свойств. Например, если два вектора направлены в одном направлении, то результат сложения будет иметь большую длину, чем каждый из отдельных векторов.
- Умножение на скаляр - вектор можно умножить на число, известное как скаляр. Эта операция изменяет длину вектора, но сохраняет его направление. Если скаляр отрицательный, то направление вектора будет изменено на противоположное.
- Единичный (нормированный) вектор - это вектор, который имеет длину равную единице. Единичные векторы обычно используются для определения направления без учета масштаба.
Эти свойства векторов в геометрии играют важную роль при решении различных задач, связанных с расположением точек и объектов в пространстве. Они позволяют определить направление и перемещение векторов, что в свою очередь помогает понять и анализировать различные геометрические ситуации.
Составляющие вектора
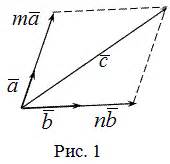
В зависимости от выбранной системы координат, вектор может иметь различные составляющие. Наиболее распространенные системы координат - прямоугольная и полярная системы координат.
В прямоугольной системе координат вектор разлагается на две составляющие - горизонтальную и вертикальную. Горизонтальная составляющая определяет изменение вектора вдоль оси Х, а вертикальная составляющая - вдоль оси Y.
В полярной системе координат вектор может быть разложен на радиальную и угловую составляющую. Радиальная составляющая определяет изменение вектора в направлении от начала координат до его конца, а угловая составляющая - угол между положительным направлением оси X и вектором.
При разложении вектора на составляющие, можно определить какая составляющая вносит больший вклад в его направление и длину. Это позволяет более точно описывать перемещение и изменение объектов в геометрии.
Основные компоненты вектора

Основные компоненты вектора включают:
1. Направление:
Направление вектора – это линия, на которой лежит точка начала и точка конца вектора. Определяется с помощью угла, который вектор образует с какой-либо фиксированной осью или направлением.
2. Длина:
Длина вектора – это величина, которая определяется расстоянием от точки начала до точки конца вектора. Величина длины вектора может быть измерена с использованием различных единиц измерения, таких как метры, сантиметры или пиксели.
3. Величина:
Величина вектора – это численное значение, которое характеризует вектор. Она может быть положительной или отрицательной и определяет силу, скорость, ускорение или другую физическую характеристику, которую представляет вектор.
4. Начало и конец:
Начало и конец вектора – это точки, которые определяют его положение и направление. Начало вектора – это точка, из которой начинается измерение его длины и направления. Конец вектора – это точка, в которой заканчивается его длина и направление.
Учитывая эти основные компоненты, векторы могут быть использованы для решения различных задач и применяются в разных областях науки и техники, включая физику, математику, компьютерную графику и дизайн.
Взаимное расположение компонент вектора

Векторы в геометрии представляют собой направленные отрезки, которые имеют определенную длину и направление. Каждый вектор может быть разложен на две или более компоненты, которые указывают на его направление в разных осях координатной системы.
Взаимное расположение компонент вектора зависит от выбора системы координат. В системе координат с двумя осями (например, оси X и Y) вектор может иметь только две компоненты, которые указывают на его направление по осям X и Y. В системе координат с тремя осями (например, оси X, Y и Z) вектор может иметь три компоненты, которые указывают на его направление по осям X, Y и Z.
Каждая компонента вектора может быть представлена числом или символической переменной, которая определяет длину этой компоненты. Например, вектор может иметь компоненты (3, 4) в двумерной системе координат, что означает, что вектор указывает на направление, образуя угол 45 градусов с положительным направлением оси X и имеющий длину 5.
Взаимное расположение компонент вектора также может быть представлено графически с помощью диаграммы векторов. Каждая компонента вектора изображается как отрезок на диаграмме с началом в начале вектора. Длина каждого отрезка соответствует длине соответствующей компоненты, а угол между отрезками указывает на направление вектора.
Взаимное расположение компонент вектора влияет на поведение и свойства вектора в геометрии. Например, если компоненты вектора имеют одинаковые знаки, то вектор будет направлен в одном направлении, в противном случае - в противоположных направлениях. Кроме того, сумма компонент вектора даст его общую длину, а угол между компонентами определит направление вектора.
Векторные операции

Сложение векторов осуществляется путем сложения соответствующих координат векторов. Если имеется два вектора A = (a₁, a₂, a₃) и B = (b₁, b₂, b₃), то их сумма A + B = (a₁ + b₁, a₂ + b₂, a₃ + b₃).
Вычитание векторов производится путем вычитания соответствующих координат. Если имеется два вектора A = (a₁, a₂, a₃) и B = (b₁, b₂, b₃), то их разность A - B = (a₁ - b₁, a₂ - b₂, a₃ - b₃).
Умножение вектора на число осуществляется умножением каждой координаты вектора на заданное число. Если имеется вектор A = (a₁, a₂, a₃) и число k, то произведение вектора на число kA = (ka₁, ka₂, ka₃).
Скалярное произведение векторов вычисляется путем умножения соответствующих координат векторов и последующей суммирования полученных произведений. Если имеется два вектора A = (a₁, a₂, a₃) и B = (b₁, b₂, b₃), то их скалярное произведение A · B = a₁b₁ + a₂b₂ + a₃b₃.
Векторное произведение векторов вычисляется с использованием правила правой руки и определяет новый вектор, перпендикулярный плоскости, образованной исходными векторами. Если имеется два вектора A = (a₁, a₂, a₃) и B = (b₁, b₂, b₃), то их векторное произведение A × B = (a₂b₃ - a₃b₂, a₃b₁ - a₁b₃, a₁b₂ - a₂b₁).
| Операция | Описание | Пример |
|---|---|---|
| Сложение | Сумма двух векторов | A + B = (a₁ + b₁, a₂ + b₂, a₃ + b₃) |
| Вычитание | Разность двух векторов | A - B = (a₁ - b₁, a₂ - b₂, a₃ - b₃) |
| Умножение на число | Умножение каждой координаты вектора на число | kA = (ka₁, ka₂, ka₃) |
| Скалярное произведение | Сумма произведений соответствующих координат векторов | A · B = a₁b₁ + a₂b₂ + a₃b₃ |
| Векторное произведение | Вектор, перпендикулярный плоскости, образованной исходными векторами | A × B = (a₂b₃ - a₃b₂, a₃b₁ - a₁b₃, a₁b₂ - a₂b₁) |
Сложение векторов
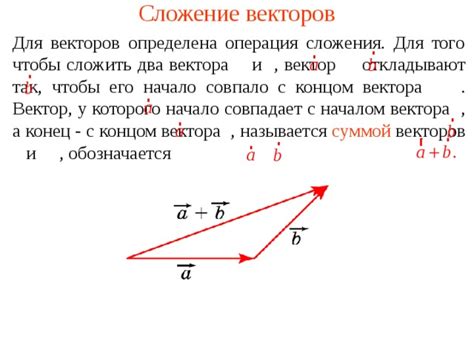
Для сложения векторов необходимо выполнить следующие шаги:
- Начать с первого вектора, определенного своей длиной и направлением.
- Определиться с направлением второго вектора и проложить его от конца первого вектора.
- Соединить начало первого вектора с концом второго вектора - получится новый вектор, который является суммой исходных векторов.
Сложение векторов также можно выполнять с использованием таблицы, где каждый столбец представляет собой компоненты вектора (например, координаты вектора в трехмерном пространстве). При сложении векторов увеличиваются соответствующие компоненты векторов.
| Компонента x | Компонента y |
|---|---|
| x1 + x2 | y1 + y2 |
Сложение векторов является основной операцией в геометрии, так как позволяет находить суммарный эффект от нескольких факторов или движений.
Определение направления вектора при сложении базируется на знании угла между исходными векторами и их относительной длины. Направление результирующего вектора может быть различным в зависимости от сочетания направлений и длин векторов.
Умножение вектора на число

Вектор можно умножить на число, получая в результате новый вектор, у которого длина и направление изменяются.
Умножение вектора на положительное число приводит к увеличению длины вектора в заданное количество раз, при этом направление остается неизменным. Например, если умножить вектор a на число k, то результатом будет вектор ka, который будет иметь длину, равную начальной длине вектора a, умноженной на k.
Умножение вектора на отрицательное число приводит к изменению его направления на противоположное, а длина остается неизменной. Таким образом, если умножить вектор a на число -k, то результатом будет вектор -ka, который будет указывать в противоположную сторону от исходного вектора, но иметь такую же длину.
Умножение вектора на ноль приводит к получению нулевого вектора, который не имеет ни направления, ни длины. Это связано с тем, что при умножении на ноль любой вектор сокращается до точки, в которой он начинался.
Умножение вектора на число является одной из основных операций в линейной алгебре и находит применение в решении множества задач в геометрии и физике.
Воздействующие факторы
Вектор в геометрии может быть определен различными способами, и его направление зависит от нескольких воздействующих факторов. Ниже приведены основные из них:
| Точка приложения | Направление вектора зависит от точки, в которой он приложен. Малейшее изменение расположения точки приложения может значительно повлиять на направление вектора. |
| Система координат | Выбор системы координат также влияет на направление вектора. В различных системах координат вектор может иметь разное направление, даже если его координаты остаются неизменными. |
| Угол поворота | Изменение угла поворота может изменить направление вектора. Вектор может быть повернут вокруг своей точки начала или конца, что приведет к изменению его направления. |
| Воздействие других векторов | Если на вектор действуют другие векторы, то его направление будет зависеть от их взаимного расположения и силы воздействия. Даже слабое изменение вектора может повлечь за собой изменение направления. |
Все эти факторы могут влиять на направление вектора в геометрии. Понимание и учет этих факторов является важным для правильного определения и использования векторов в геометрических вычислениях и проблемах.



