Объединение множеств является одной из основных операций в теории множеств. Эта операция позволяет объединить два или более множества в одно множество, включающее все элементы из исходных множеств. Таким образом, объединение множеств позволяет собрать вместе все уникальные элементы из нескольких множеств и получить их общую сумму.
В третьем классе Петерсона школьники изучают базовые операции с множествами, включая объединение. Данная операция встречается в различных областях математики, начиная от теории множеств и заканчивая компьютерными науками. Она играет важную роль при работе с данными и помогает решать различные задачи, связанные с группировкой и анализом информации.
Знание операции объединения множеств позволяет ученикам лучше понять, как работает алгоритмы сбора данных и решать сложные задачи логического анализа. Безусловно, понимание базовых операций с множествами является важным шагом на пути к развитию математического и аналитического мышления.
Объединение множеств: определение и свойства
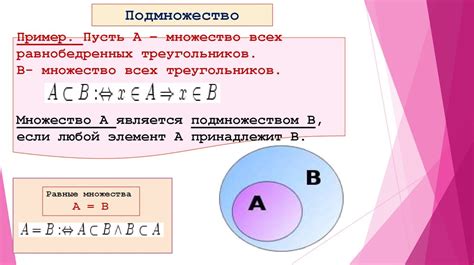
Свойства объединения множеств:
- Коммутативность: порядок объединения двух множеств не имеет значения. То есть, A ∪ B = B ∪ A.
- Ассоциативность: при объединении трех и более множеств порядок их объединения не имеет значения. То есть, (A ∪ B) ∪ C = A ∪ (B ∪ C).
- Идемпотентность: объединение множества с самим собой не изменяет это множество. То есть, A ∪ A = A.
- Дистрибутивность относительно пересечения: объединение множеств с пересечением друг с другом равно объединению отдельных множеств. То есть, A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
- Дистрибутивность относительно разности: объединение множества с разностью других множеств равно разности объединения каждого множества с этой разностью. То есть, A ∪ (B \ C) = (A ∪ B) \ (A ∪ C).
Объединение множеств может быть представлено в виде операции ∪, где A ∪ B обозначает объединение множества A и множества B.
Что такое объединение множеств
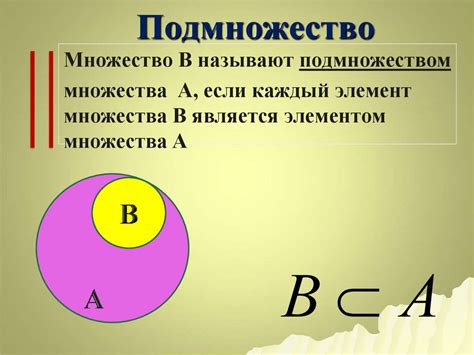
Обозначается операцией "∪" или последовательностью символов "Union" или " united ", в зависимости от способа записи. Например, объединение множеств A и B записывается как A ∪ B или A union B или A united with B.
Для объединения множеств необходимо выполнить следующие шаги:
- Взять все уникальные элементы из первого множества.
- Взять все уникальные элементы из второго множества.
- Объединить полученные элементы в новое множество.
Например, если есть множество A = {1, 2, 3} и множество B = {3, 4, 5}, то результатом их объединения будет новое множество C = {1, 2, 3, 4, 5}.
Объединение множеств применяется в различных областях математики, логики, программирования и других науках. Эта операция позволяет объединять данные или элементы из разных источников для получения общего набора информации.
Как выполняется объединение множеств

Для выполнения объединения множеств, необходимо следовать определенному алгоритму:
- Создать новое пустое множество, которое будет содержать объединение.
- Добавить все элементы из первого множества в новое множество.
- Добавить все элементы из второго множества в новое множество.
- Повторять пункт 3 для каждого следующего множества, если таковые имеются.
При выполнении объединения множеств нужно обратить внимание на два основных момента:
- Дублирующиеся элементы не добавляются в объединение. Если элемент уже содержится в объединении, то он будет проигнорирован.
- Порядок элементов в объединении не имеет значения. В результирующем множестве элементы могут следовать в произвольном порядке.
Пример:
Множество A: {1, 2, 3}
Множество B: {3, 4, 5}
Множество C: {5, 6, 7}
Объединение множеств A, B и C: {1, 2, 3, 4, 5, 6, 7}Таким образом, объединение множеств позволяет объединить элементы из нескольких множеств в одно множество без дублирования элементов и с произвольным порядком следования элементов в результирующем множестве.
Свойства объединения множеств
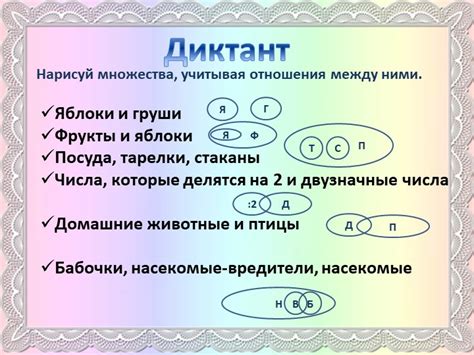
Свойства объединения множеств:
- Коммутативность: порядок объединения множеств не влияет на результат. То есть, для любых множеств A и B, A ∪ B = B ∪ A.
- Ассоциативность: объединение множеств ассоциативно. То есть, для любых множеств A, B и C, (A ∪ B) ∪ C = A ∪ (B ∪ C).
- Идемпотентность: объединение множеств с собой не меняет результат. То есть, для любого множества A, A ∪ A = A.
- Пустое множество: объединение пустого множества с любым множеством равно этому множеству. То есть, для любого множества A, A ∪ ∅ = A.
- Универсальное множество: объединение универсального множества с любым множеством равно универсальному множеству. То есть, для любого множества A, A ∪ ξ = ξ.
Объединение множеств 3 класса Петерсона обладает всеми указанными свойствами, а также дополнительными свойствами, которые присущи множествам 3 класса Петерсона.
Коммутативность объединения множеств

Для двух множеств A и B коммутативность объединения записывается как:
A ∪ B = B ∪ A
То есть, объединение множеств A и B будет содержать все элементы, которые есть в множестве A или в множестве B, вне зависимости от порядка множеств.
Например, если имеются два множества: A = {1, 2, 3} и B = {3, 4, 5}, то их объединение будет:
A ∪ B = {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5} = B ∪ A
Таким образом, коммутативность объединения множеств позволяет менять порядок множеств без влияния на результат операции объединения.
Ассоциативность объединения множеств
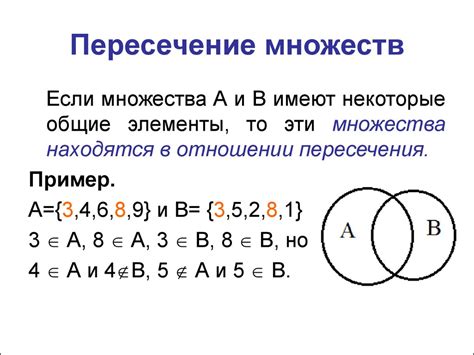
Операция объединения множеств обладает свойством ассоциативности, что означает, что результат ее применения на трех множествах не зависит от порядка, в котором она применяется.
Для любых множеств A, B и C выполнено следующее равенство:
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Геометрически это свойство можно представить с помощью диаграммы Венна: объединение множеств A, B и C образует множество, которое содержит все элементы, принадлежащие хотя бы одному из трех множеств.
Также стоит отметить, что при объединении множеств не происходит дублирования элементов. Если элемент уже содержится в одном из множеств, то он будет учтен только один раз в итоговом объединенном множестве.
Ассоциативность объединения множеств является одним из основных свойств этой операции и позволяет производить объединение множеств в любом порядке, не меняя их результат.
Примеры использования объединения множеств в классе Петерсона
Объединение множеств используется в классе Петерсона для комбинирования элементов из различных множеств и создания нового множества, которое содержит все уникальные элементы из исходных множеств.
Рассмотрим пример использования объединения множеств на наборе данных:
Множество A: {1, 2, 3, 4}
Множество B: {3, 4, 5, 6}
Множество C: {4, 5, 6, 7}
В данном примере мы имеем три множества: A, B и C. Используя операцию объединения множеств, мы можем создать новое множество D, которое будет содержать все уникальные элементы из множеств A, B и C:
Множество D: {1, 2, 3, 4, 5, 6, 7}
Таким образом, объединение множеств позволяет нам собрать все уникальные элементы из нескольких множеств в одно общее множество. Это может быть полезно, например, при работе с базами данных, где требуется объединение результатов запросов из разных таблиц.



