Математические функции описывают зависимость одной величины от другой. Одним из способов классификации функций является разделение их на четные и нечетные. Эта классификация основывается на свойствах функции относительно оси абсцисс.
Четная функция - это такая функция, у которой значения симметричны относительно оси абсцисс. Иными словами, значение функции в точке x равно значению функции в точке -x. График четной функции симметричен относительно оси y. Некоторые примеры четных функций: косинус, модульный квадрат, некоторые параболы.
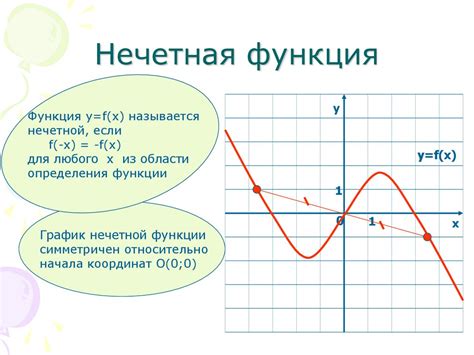
Нечетная функция - это такая функция, у которой значения антисимметричны относительно оси абсцисс. То есть значение функции в точке x равно противоположному значению функции в точке -x. График нечетной функции симметричен относительно начала координат O(0,0). Примеры нечетных функций: синус, линейная функция с нулевым свободным членом.
Четная функция: основные характеристики
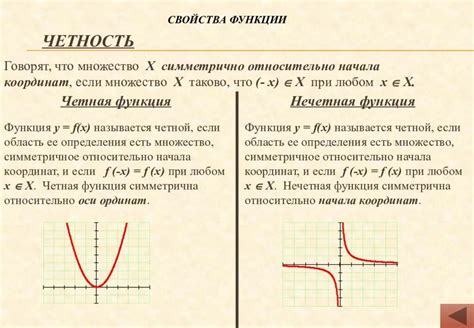
- Симметрию относительно оси ординат: если точка (x, y) принадлежит графику четной функции, то точка (-x, y) также принадлежит графику этой функции.
- Ось симметрии: у четной функции осью симметрии служит ось ординат (y-ось), поскольку график функции симметричен относительно нее.
- Четную функцию можно представить в виде суммы только четных степеней переменной: f(x) = a₀ + a₂x² + a₄x⁴ + ... + a₂𝑛x²𝑛, где a₀, a₂, a₄, ..., a₂𝑛 - коэффициенты функции.
- Примеры четных функций: парабола (f(x) = x²), косинус (f(x) = cos(x)), модуль квадратичной функции (f(x) = |x²|) и т.д.
Четные функции широко используются в математике и естественных науках, так как они обладают определенными свойствами, упрощающими анализ и решение уравнений. Также они являются важным инструментом в физике и инженерии для моделирования и предсказания различных явлений.
Определение, свойства и примеры

Четная функция - это функция, которая обладает особой симметрией, называемой четностью. Для четной функции значение функции в точке x равно значению функции в точке -x. Математически это можно записать следующим образом: f(x) = f(-x).
Свойства четных функций:
- График четной функции симметричен относительно оси y.
- Если функция задана в виде аналитической формулы, то в ней могут присутствовать только четные степени переменной.
- Примеры четных функций: cos(x), x^2, |x|.
Нечетная функция - это функция, которая обладает особой симметрией, называемой нечетностью. Для нечетной функции значение функции в точке x равно противоположному значению функции в точке -x. Математически это можно записать следующим образом: f(x) = -f(-x).
Свойства нечетных функций:
- График нечетной функции симметричен относительно начала координат.
- Если функция задана в виде аналитической формулы, то в ней могут присутствовать только нечетные степени переменной.
- Примеры нечетных функций: sin(x), x^3, sqrt(x).
Четные и нечетные функции являются важной концепцией в математике и широко применяются в различных областях, таких как физика, экономика и инженерия.
Нечетная функция: основные характеристики
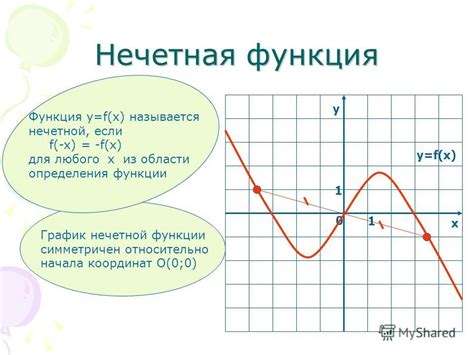
Основные характеристики нечетной функции включают следующее:
- График нечетной функции симметричен относительно начала координат. Точка (-x, -y) на графике соответствует точке (x, y).
- Если функция f(x) нечетная и задана на всей числовой оси, то f(0) = 0.
- Примеры нечетных функций включают функции синуса (sin(x)), косинуса (cos(x)), тангенса (tan(x)), котангенса (ctg(x)), арксинуса (arcsin(x)), арккосинуса (arccos(x)), арктангенса (arctan(x)) и другие.
Нечетные функции находят широкое применение в различных математических и физических моделях, а также играют важную роль в анализе и инженерии. Изучение свойств нечетных функций позволяет более глубоко понять их поведение и использовать их эффективно в практических задачах.
Определение, свойства и примеры

Нецное понятие функции описывает такую функцию, для которой значение функции при замене аргумента на его отрицание будет отрицанием значения функции для исходного аргумента. Это означает, что если значение функции для аргумента x равно f(x), то значение функции для -x будет равно -f(x).
Основные свойства четных и нечетных функций следующие:
| Свойство | Четная функция | Нечетная функция |
|---|---|---|
| Определение | f(x) = f(-x) | f(x) = -f(-x) |
| График | Симметричен относительно оси y | Симметричен относительно начала координат |
| Интеграл | Интеграл на симметричном интервале равен нулю | Интеграл на симметричном интервале равен нулю |
Примеры четных функций:
- f(x) = x2
- f(x) = |x|
- f(x) = cos(x)
Примеры нечетных функций:
- f(x) = x
- f(x) = sin(x)
- f(x) = ex
Отличия между четными и нечетными функциями
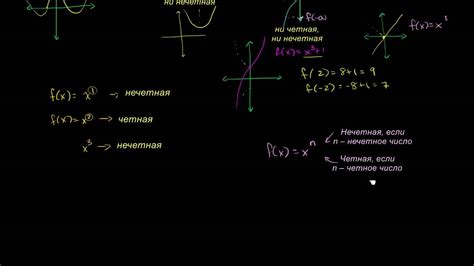
Четная функция - это функция, которая обладает осевой симметрией относительно оси ординат. Это означает, что значение функции для аргумента x равно значению функции для аргумента -x. Следовательно, график четной функции симметричен относительно оси ординат. Примером четной функции является f(x) = x^2, где значение функции f(x) равно квадрату аргумента x.
Нечетная функция - это функция, которая обладает осевой симметрией относительно начала координат. Это означает, что значение функции для аргумента x равно значению функции для аргумента -x с противоположным знаком. Следовательно, график нечетной функции симметричен относительно начала координат. Примером нечетной функции является f(x) = x^3, где значение функции f(x) равно кубу аргумента x.
Отличия между четными и нечетными функциями включают:
- Симметрию графика функции: четные функции симметричны относительно оси ординат, а нечетные функции - относительно начала координат.
- Свойства значений функции: значения четной функции для аргументов x и -x равны, в то время как значения нечетной функции для аргументов x и -x обладают противоположным знаком.
- Поведение функции в окрестности нуля: для четной функции f(x), f(0) = f(-0), а для нечетной функции g(x), g(0) = -g(-0).
- Часто четные функции содержат только четные степени x, а нечетные функции - только нечетные степени x.
Знание отличий между четными и нечетными функциями помогает в понимании и анализе их свойств, а также в решении математических задач и построении графиков функций.
Сравнение по свойствам и графикам
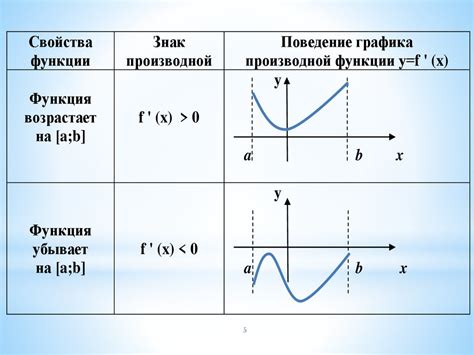
Четная и нечетная функции имеют некоторые общие свойства, но они также различаются по некоторым характеристикам.
Общие свойства четных и нечетных функций:
- Функции могут быть определены для всех действительных значений аргумента.
- Графики функций симметричны относительно оси ординат (ось симметрии).
- Для каждой точки (x, y) на графике функции, точка (-x, y) также принадлежит графику.
Характеристики четных функций:
- Значение функции f(x) равно значению функции f(-x) для любого значения x.
- На графике четной функции точки симметричны как по оси ординат, так и по оси абсцисс (начало координат является точкой симметрии).
- Примеры четных функций: cos(x), x^2.
Характеристики нечетных функций:
- Значение функции f(x) равно противоположному значению функции f(-x) для любого значения x.
- На графике нечетной функции точки симметричны только относительно начала координат (ось ординат является осью симметрии).
- Примеры нечетных функций: sin(x), x^3.
Примеры четных функций
Ниже приведены примеры четных функций:
- Парабола с вершиной в начале координат: f(x) = x^2
- Косинусная функция: f(x) = cos(x)
- Модуль функции: f(x) = |x|
- Произведение четных функций: f(x) = x^2 * cos(x)
Эти примеры демонстрируют, что четные функции могут быть разными по своему виду и характеру, но все они обладают общим свойством симметрии относительно оси ординат.
Популярные примеры и их особенности

f(-x) = f(x)
Эта функция симметрична относительно оси ординат и при этом принимает лишь положительные значения на промежутке [0, π/2] и отрицательные значения на промежутке [π/2, π].
Нечетной функцией является функция синуса. Синус обладает свойством:
f(-x) = -f(x)
Функция синуса также симметрична относительно начала координат и принимает положительные значения на промежутке (0, π/2) и отрицательные значения на промежутке (-π/2, 0).
Другими примерами четных функций могут служить парабола, гипербола симметричная относительно оси ординат. Примерами нечетных функций являются гипербола несимметричная относительно начала координат и график функции арктангенса.
Знание особенностей четных и нечетных функций позволяет решать множество задач из разных областей, таких как физика, математика, экономика и др.



