Пересечение двух плоскостей - это область математики, где изучаются точки, которые находятся на пересечении двух плоскостей в трехмерном пространстве. Эта тема имеет большое значение в геометрии, инженерии и других научных областях. Пересечение плоскостей обладает рядом уникальных свойств и характеристик, которые помогают в решении различных задач и проблем.
Пересечение двух плоскостей может быть представлено в виде прямой, точки или общей плоскости. Одна из основных характеристик пересечения плоскостей - это угол между плоскостями. Угол может быть острый, прямой или тупой, в зависимости от взаимного положения плоскостей.
Одним из важных свойств пересечения двух плоскостей является наличие или отсутствие общих точек. Если плоскости пересекаются, то общими точками будут линия, прямая или даже плоскость. Если плоскости не пересекаются, то общих точек не будет.
Важно отметить, что пересечение двух плоскостей может быть рассмотрено в различных геометрических системах, таких как евклидова геометрия, сферическая геометрия или геометрия Лобачевского. В каждой из них свой набор свойств и характеристик пересечения плоскостей.
Характеристики пересечения двух плоскостей
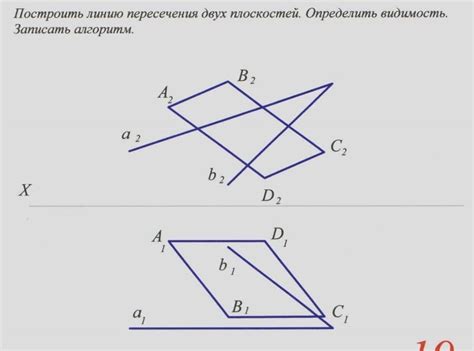
Возможные характеристики пересечения двух плоскостей включают:
1. Точка: Если две плоскости пересекаются только в одной точке, то это является наиболее простым случаем пересечения. Точка пересечения определяется как общая точка прямых линий пересечения двух плоскостей. Эта точка может быть описана своими координатами в трехмерном пространстве.
2. Линия: Если две плоскости пересекаются по прямой линии, то это является более сложным случаем пересечения. Линия пересечения является линией, которая лежит в обоих плоскостях и проходит через общую точку пересечения.
3. Плоскость: Если две плоскости пересекаются по плоскости, то это является наиболее сложным случаем пересечения. Плоскость пересечения является плоскостью, которая лежит в обоих плоскостях и проходит через общую линию пересечения. Плоскость может быть описана уравнением в трехмерном пространстве.
Ориентация и расположение плоскостей также могут оказывать влияние на свойства и характеристики пересечения. Например, плоскости могут быть параллельными и не пересекаться, они могут быть скрещивающимися и иметь только одну точку пересечения, или они могут быть наклонными и образовывать угол в пересечении.
Исследование и понимание характеристик пересечения двух плоскостей является важным аспектом геометрии и пространственного анализа, так как это позволяет анализировать и моделировать различные физические и геометрические явления.
Место пересечения

Если плоскости пересекаются, то у них есть общая точка, которая может быть одна или бесконечно много, в зависимости от взаимного расположения плоскостей.
Если плоскости имеют общую точку, то они называются скрещивающимися или пересекающимися. В этом случае они не обладают никакими особыми свойствами и просто пересекаются в какой-то точке.
Место пересечения плоскостей может быть выражено аналитически с помощью системы уравнений плоскостей. Для этого необходимо решить систему уравнений и найти координаты общей точки.
Если плоскости не имеют общих точек, то они называются параллельными. Параллельные плоскости могут быть строго параллельными, то есть не пересекаются ни в одной точке, или совпадать, то есть иметь бесконечно много общих точек.
Важно отметить, что место пересечения двух плоскостей не всегда существует. Например, если плоскости параллельны, то они не имеют общей точки и, следовательно, их место пересечения не существует.
Место пересечения плоскостей имеет важное значение в геометрии и в различных областях приложений, таких как инженерия, архитектура и компьютерная графика. Знание свойств и характеристик места пересечения плоскостей помогает решать задачи и строить модели, основанные на пересечении плоскостей.
Угол между плоскостями
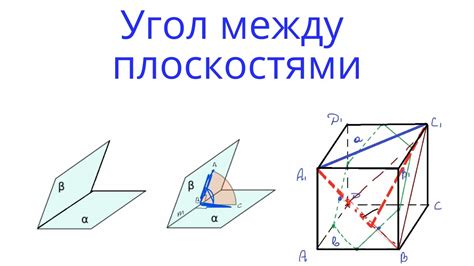
Нормаль к плоскости - вектор, перпендикулярный плоскости. Для двух плоскостей с нормалями n₁ и n₂ соответственно, угол между плоскостями определяется как угол между этими нормалями.
Угол между плоскостями можно вычислить с помощью скалярного произведения нормалей:
cos(α) = (n₁ · n₂) / (|n₁| |n₂|)
где α - угол между плоскостями, · - скалярное произведение, |n₁| и |n₂| - длины векторов нормалей.
Если нормали плоскостей единичные векторы, то можем упростить эту формулу:
cos(α) = n₁ · n₂
Угол между плоскостями может иметь значения от 0 до 180 градусов. Когда угол равен 0, плоскости совпадают. Когда угол равен 180 градусам, плоскости параллельны, но направление нормалей противоположно.
Угол между плоскостями может использоваться для определения взаимного расположения объектов в пространстве. Например, угол между плоскостью, заданной поверхностью стола, и плоскостью, заданной поверхностью тела, может определить, находится ли тело на столе или не соприкасается ли с ним.
Знание угла между плоскостями также имеет практическое значение для решения задач в геометрическом моделировании, компьютерной графике и других областях, связанных с трехмерной геометрией.
Линия пересечения плоскостей
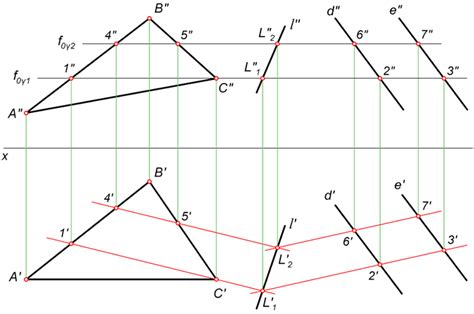
Линия пересечения может иметь различную направленность и форму. Она может быть вертикальной, горизонтальной, наклонной или даже принимать форму кривой. Форма и направленность линии пересечения определяются углами, под которыми плоскости пересекаются друг с другом.
Если плоскости пересекаются под острым углом, линия пересечения будет прямой линией. Если угол между плоскостями составляет 90 градусов, линия пересечения будет параллельна одной из осей координат. При наклонном пересечении, линия будет иметь форму кривой.
Линия пересечения двух плоскостей важна во многих областях, таких как геометрия, физика, инженерия и аэродинамика. Знание характеристик и свойств линии пересечения плоскостей позволяет более точно предсказывать и анализировать результаты пересечения двух плоскостей.



