Дроби - одна из основных тем в математике, которую мы изучаем уже на ранних ступенях образования. Многие из нас помнят непростые вопросы на уроках математики, связанные с дробями. Но зачастую мы забываем о том, что дроби - это не просто числа, а математическое понятие, имеющее свои особенности и свойства.
Одно из основных свойств дробей - их проявление и описание. Дроби являются частью числовой прямой, расположенной между целыми числами. Они представляют собой доли от целого числа и представляются в виде дробей, где числитель - это количественная часть, а знаменатель - это количественная единица. Например, дробь 1/2 означает, что имеется одна половина от целого числа.
Математические дроби имеют множество приложений в различных областях науки и жизни. Они позволяют нам точно и удобно выражать доли, долги, отношения и доли процента. Да и в повседневной жизни мы сталкиваемся с дробями: при дележе пиццы на части, измерении времени, расчете скидки и т.д.
Что такое дробь?
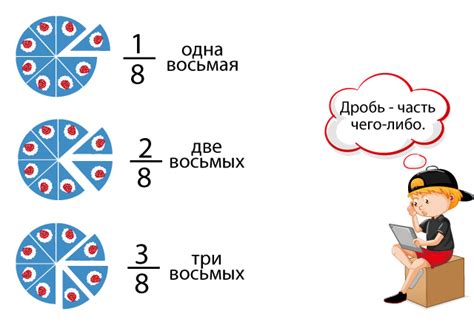
Дроби применяются в различных областях математики, физики, химии и других наук. Они позволяют точно описывать доли, доли процента, координаты на числовой оси, вероятности и другие сущности, которые не представляют собой целые числа.
Кроме того, дроби являются основой для дальнейших математических операций, таких как сложение, вычитание, умножение и деление. Они позволяют сравнивать и складывать доли, выполнять расчеты с долями и решать различные задачи.
Для наглядного представления и работы с дробями часто используются таблицы. В таблице числитель и знаменатель представлены в виде отдельных ячеек, что облегчает их сравнение, сложение и вычитание.
| Числитель | Знаменатель |
|---|---|
| 1 | 2 |
| 3 | 4 |
| 5 | 6 |
Это основная информация о дробях. Они позволяют представлять доли и выполнение различных операций с ними. Знание и понимание дробей имеет важное значение в образовании и повседневной жизни.
Описание понятия и основные характеристики

Основные характеристики дробей:
- Числитель - это число, расположенное над чертой. Он указывает на то, сколько частей мы имеем или рассматриваем.
- Знаменатель - это число, расположенное под чертой. Он показывает, сколько частей было разделено целое число.
- Целая часть - это целое число, которое больше или равно единице и добавляется к дроби. Она представляет собой число целых частей внутри дроби.
- Десятичное представление - это представление дроби в виде десятичной дроби. Оно получается путем деления числителя на знаменатель.
- Десятичная дробь - это дробь, где знаменатель является степенью 10, например, 0.25 или 0.75.
- Виды дробей - дроби могут быть обыкновенными (не имеющими целой части) или смешанными (содержащими целую часть).
Понимание и использование дробей в математике важно при работе с долями, процентами, различными единицами измерения и другими математическими операциями. Понимание основных характеристик дробей позволяет более эффективно работать с ними и применять их в реальных ситуациях.
Основное свойство дроби

Пример:
| Дробь | Числитель | Знаменатель |
|---|---|---|
| 1/2 | 1 | 2 |
| 3/4 | 3 | 4 |
| 2/5 | 2 | 5 |
Как видно из примеров, дробь 1/2 представляет половину от целого, дробь 3/4 – три четверти, а дробь 2/5 – две пятые. Таким образом, основное свойство дроби позволяет нам описывать доли от целых чисел и использовать их в различных контекстах, например, в математических вычислениях, физических задачах или финансовом планировании.
Проявление в математике и повседневной жизни

В математике дроби используются для представления долей и частей чисел. Они позволяют точно указывать на доли объектов или явлений, таких как часть целого числа, доля величины или отношение двух величин. Дроби используются в различных областях математики, включая алгебру, геометрию и статистику.
В повседневной жизни дроби приобретают особенное значение, например, при расчете доли скидки на товары в магазине или при дележе блюд между людьми. Они также используются для измерения времени, когда указывается доля часа или минуты, а также в кулинарии, где дроби используются для измерения объемов ингредиентов.
Проявление дробей в математике и повседневной жизни подчеркивает их важность и неотъемлемую роль в нашей жизни. Они помогают нам более точно и точно описывать и измерять различные явления и объекты, а также выполнять различные вычисления и расчеты. Понимание дробей и их свойств позволяет нам более глубоко понять окружающий мир и применять свои математические навыки в реальной жизни.
Как описать дробь?
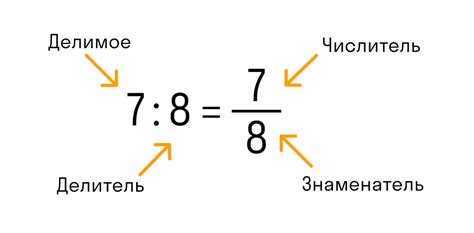
Для полного описания дроби также нужно указать ее тип. Дроби могут быть правильными, неправильными и смешанными. Правильная дробь - это дробь, у которой числитель меньше знаменателя. Неправильная дробь - это дробь, у которой числитель больше или равен знаменателю. Смешанная дробь - это комбинация целой части и правильной дроби.
Примеры:
- Правильная дробь: 2/3
- Неправильная дробь: 5/4
- Смешанная дробь: 1 1/2
Дроби также могут быть эквивалентными, то есть представлять одно и то же значение, но записанные различными образами. Для определения эквивалентных дробей необходимо сократить дробь до наименьших частей, то есть числитель и знаменатель должны быть взаимно простыми числами.
Описание дробей является важной частью математики и используется в различных областях знаний. Понимание свойств и способов описания дробей является фундаментальным для дальнейшего изучения математики и ее применения в реальных ситуациях.



