Трапеция - это четырехугольник, у которого две противоположные стороны параллельны. Одно из свойств трапеции заключается в том, что сумма длин двух ее оснований равна сумме длин боковых сторон. Но что делать, если нам нужно доказать, что основания трапеции равны по длине? В этой статье мы рассмотрим одно из возможных доказательств на основе подобия треугольников.
Предположим, что у нас есть трапеция ABCD, в которой AB и CD - ее основания. Нам нужно доказать, что |AB| = |CD|. Для начала, обратим внимание на то, что в трапеции достаточно много пар треугольников, построенных на ее сторонах: ABD и BCD, ABC и BCD, ACD и BCD. Обратимся к паре треугольников ABC и BCD.
Будучи трапецией, у которой AB и CD равны, треугольники ABC и BCD имеют общую сторону BC. Поскольку BD параллельна AC (по определению трапеции), то треугольники ABC и BCD, как известно из геометрии, подобны. Поэтому, соответствующие стороны треугольников, то есть |AB| и |CD|, должны быть пропорциональны. Но так как треугольники подобны, их пропорциональность означает, что их стороны пропорциональны по длине. Значит, |AB| = |CD|, что и требовалось доказать.
Типы трапеций
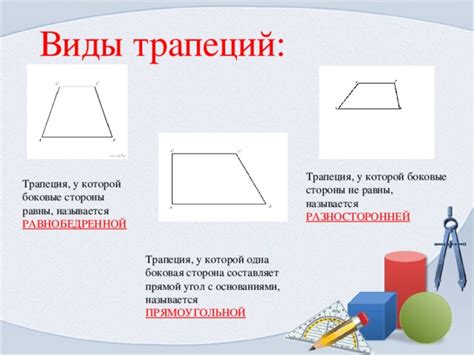
1. Равнобедренная трапеция
В равнобедренной трапеции основания равны, а боковые стороны равны друг другу. Также в этом типе трапеции углы на основаниях равны. Равнобедренная трапеция имеет одну ось симметрии, которая проходит через середину каждой боковой стороны и перпендикулярна основаниям.
2. Прямоугольная трапеция
Прямоугольная трапеция - это трапеция, у которой один из углов между основаниями является прямым углом. Это означает, что противоположные стороны трапеции параллельны и равны друг другу, а также углы на основаниях являются смежными.
3. Равносторонняя трапеция
Равносторонняя трапеция - это трапеция, у которой все стороны равны. В равносторонней трапеции все углы на основаниях равны и равны 60 градусам. Такой тип трапеции является особым случаем правильного многоугольника.
4. Прямоугольно-равнобедренная трапеция
Прямоугольно-равнобедренная трапеция - это трапеция, у которой одно из оснований является перпендикуляром к боковой стороне, а другое основание и другая боковая сторона равны. Углы на основаниях такой трапеции равны.
Условия равенства оснований

Условия равенства оснований:
| Условие | Объяснение |
|---|---|
| 1 | Длины одной основания равны. |
| 2 | Длины других сторон также равны. |
| 3 | Углы при основаниях равны. |
| 4 | Диагонали трапеции равны. |
Только при выполнении всех указанных условий мы можем сказать, что две трапеции равны построению. Эти условия позволяют нам определить подобные треугольники и применять соответствующие свойства при доказательстве геометрических утверждений.
Свойства равенства треугольников
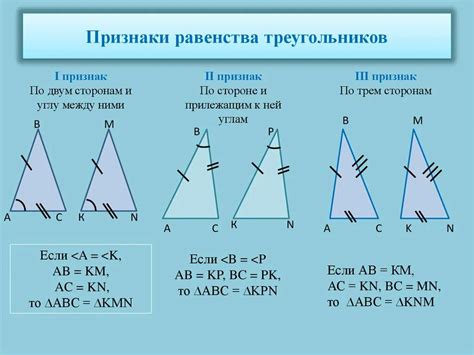
Теорема 1: Если у двух треугольников все стороны равны соответственно, то треугольники равны.
Доказательство: Пусть даны два треугольника ABC и DEF, у которых AB = DE, BC = EF и AC = DF. Возьмем точку G на AB, такую что AG = DE. Соединим точки G и C.
Так как AB = DE и AG = DE, то AG = GC.
Также, так как BC = EF и GC = EF, то GC = CF.
Значит, AG = GC = CF. Из этого следует, что треугольники AGC и CFE равны двух сторон и углу, так как угол AGC = угол CFE.
Из теоремы о равенстве треугольников по двум сторонам и углу следует, что треугольники ACG и DEF равны. Но тогда и треугольники ABC и DEF равны, так как они оба содержат одинаковые треугольники ACG и DEF.
Таким образом, если у двух треугольников все стороны равны соответственно, то треугольники равны.
Теорема 2: Если у двух треугольников равны две стороны и один угол между ними, то треугольники равны.
Доказательство: Пусть даны два треугольника ABC и DEF, у которых AB = DE, BC = EF и угол BAC = угол EDF. Рассмотрим отрезок ED.
Так как AB = DE и BC = EF, то AB + BC = DE + EF. Следовательно, AC = DF.
Также, так как угол BAC = угол EDF, то треугольники ABC и DEF подобны согласно признаку на равенство двух углов.
Пусть точка G лежит на отрезке AB и AG = DE. Соединим точки G и C.
Так как AB = DE и AG = DE, то AG = GC.
Также, так как BC = EF и GC = EF, то GC = CF.
Значит, AG = GC = CF. Из этого следует, что треугольники AGC и CFE равны двух сторон и углу, так как угол AGC = угол CFE.
Из теоремы о равенстве треугольников по двум сторонам и углу следует, что треугольники ACG и DEF равны. Но тогда и треугольники ABC и DEF равны, так как они оба содержат одинаковые треугольники ACG и DEF.
Таким образом, если у двух треугольников равны две стороны и один угол между ними, то треугольники равны.
Теоремы о подобии треугольников
- Теорема AA (угл-угл): Если два угла одного треугольника равны соответственно двум углам другого треугольника, то эти треугольники подобны.
- Теорема SAS (сторона-угл-сторона): Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а угол между этими сторонами равен, то эти треугольники подобны.
- Теорема SSS (сторона-сторона-сторона): Если все стороны одного треугольника пропорциональны всем сторонам другого треугольника, то эти треугольники подобны.
- Теорема RHS (прямоугольник-гипотенуза-сторона): Если гипотенуза и одна из катетов одного прямоугольного треугольника пропорциональны гипотенузе и одному из катетов другого прямоугольного треугольника, то эти треугольники подобны.
- Теорема SAA (сторона-угол-угол): Если две стороны одного треугольника пропорциональны двум углам другого треугольника, то эти треугольники подобны.
Вышеуказанные теоремы позволяют нам установить подобие треугольников и использовать его для решения разнообразных задач и построений в геометрии.
Доказательство равенства оснований
Для доказательства равенства оснований трапеции воспользуемся свойствами подобных треугольников. Предположим, что даны две трапеции ABCD и EFGH с основаниями AB и EF соответственно. Нам нужно показать, что AB = EF.
Рассмотрим треугольники ABC и EFG, которые образуются с основаниями AB и EF. По свойству подобия треугольников, мы знаем, что их соответствующие стороны пропорциональны. То есть:
| AB | BC | AC |
| : | : | : |
| EF | FG | EG |
Так как треугольники ABC и EFG подобны, мы можем написать следующее соотношение:
AB/EF = BC/FG = AC/EG
Нам известно, что сторона BC равна стороне FG, так как это боковая сторона трапеции. Также, известно, что сторона AC равна стороне EG, так как это другая боковая сторона трапеции. Поэтому, мы можем записать:
AB/EF = 1 = AC/EG
Из этого выражения следует, что AB = EF. Таким образом, мы доказали равенство оснований трапеции ABCD и EFGH.
Примеры задач на доказательство равенства оснований

- Дана трапеция ABCD, где AB



