Основание в восьмеричной системе счисления определяет количество различных цифр, которые используются для представления чисел. В данной системе используются восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричная система счисления является позиционной, что означает, что значение каждой цифры зависит от ее позиции в числе.
Основание является важным понятием в восьмеричной системе счисления, поскольку оно определяет основу выполнения математических операций в данной системе. Например, при выполнении сложения или умножения чисел в восьмеричной системе, необходимо учитывать основание системы.
Примеры использования восьмеричной системы счисления могут быть найдены в различных областях. Например, в информатике она используется при работе с битовыми операциями и с памятью компьютера. Восьмеричная система может быть полезной при выполнении преобразований или измерений в электронике или физике.
Основание в восьмеричной системе: значение и примеры

Основание 8 означает, что система содержит восемь цифр, и она является одной из часто используемых систем счисления. Она широко применяется в программировании, в том числе для представления битовых масок и флагов.
Для примера, давайте рассмотрим число 378 в восьмеричной системе счисления. Это число можно представить в десятичной системе счисления следующим образом:
| Позиция | 7 | 3 |
|---|---|---|
| Вес | 81 | 80 |
Чтобы перевести число 378 в десятичную систему счисления, мы умножаем каждую цифру числа на вес ее позиции и складываем результаты. В данном случае, это будет: (3 * 81) + (7 * 80) = 24 + 7 = 31.
Таким образом, число 378 в десятичной системе счисления равно 31.
Что такое основание в восьмеричной системе счисления?

Восьмеричная система счисления использует восемь цифр - от 0 до 7. Каждая цифра представляет определенную степень числа 8. Например, число 123 в восьмеричной системе счисления представляет собой:
1 * 8^2 + 2 * 8^1 + 3 * 8^0 = 64 + 16 + 3 = 83.
Основание влияет на способ записи и интерпретацию чисел. При использовании восьмеричной системы счисления, каждая цифра в числе имеет вес, равный степени основания, возведенной в соответствующую позицию цифры. Это позволяет более компактно записывать и передавать большие числа в компьютерных системах.
Как работает восьмеричная система счисления?

Восьмеричная система счисления широко используется в программировании, особенно при работе с компьютерами и операционными системами. Как и в двоичной системе, числа в восьмеричной системе счисления представляются последовательностью цифр, называемой восьмеричным числом. Это число имеет свою степень и вес каждого разряда. Например, восьмеричное число 2375 состоит из разрядов: 2 в разряде 10^2, 3 в разряде 10^1 и 5 в разряде 10^0.
Восьмеричная система счисления также может быть преобразована в другие системы счисления, такие как десятичная и двоичная, и наоборот. Для этого используются специальные правила и алгоритмы, которые позволяют переводить числа из одной системы в другую.
Например, пусть у нас есть восьмеричное число 53. Чтобы перевести его в десятичную систему счисления, нужно умножить каждую цифру числа на 8 в степени, соответствующей ее положению, и сложить полученные произведения для каждого разряда. В данном случае: 5 * 8^1 + 3 * 8^0 = 40 + 3 = 43.
Таким образом, восьмеричная система счисления предоставляет удобный способ представления чисел, особенно в информатике. Она позволяет компактно хранить числовые значения и выполнять различные математические операции. Поэтому понимание и использование восьмеричной системы счисления являются важными навыками для программистов и специалистов в области компьютерных наук.
Значение основания в восьмеричной системе

В восьмеричной системе счисления основание составляет 8. Это означает, что восьмеричная система использует 8 различных цифр для представления чисел: 0, 1, 2, 3, 4, 5, 6 и 7.
Восьмеричная система удобна для работы с компьютерными данными, так как каждая восьмеричная цифра эквивалентна трём двоичным цифрам. Таким образом, восьмеричное число проще представить в виде двоичного числа и наоборот.
Например, восьмеричное число 14 в двоичной системе счисления будет равно 1110. Каждая цифра в восьмеричном числе заменяется на соответствующие ей три двоичных цифры.
| Восьмеричная цифра | Двоичное представление |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Таким образом, основание в восьмеричной системе счисления, равное 8, обладает своей уникальной особенностью, с помощью которой можно эффективно представлять и обрабатывать числа.
Как преобразовать число из восьмеричной системы в десятичную?
Для преобразования числа из восьмеричной системы счисления в десятичную, каждую цифру в числе нужно умножить на соответствующую степень основания и сложить полученные значения.
Например, рассмотрим число 753 в восьмеричной системе. Для преобразования его в десятичную систему, нужно умножить каждую цифру на соответствующую степень числа 8:
7 * 8^2 + 5 * 8^1 + 3 * 8^0 = 7 * 64 + 5 * 8 + 3 = 448 + 40 + 3 = 491
Таким образом, число 753 в восьмеричной системе равно числу 491 в десятичной системе.
Аналогично можно преобразовать любое число из восьмеричной системы в десятичную, следуя тому же принципу.
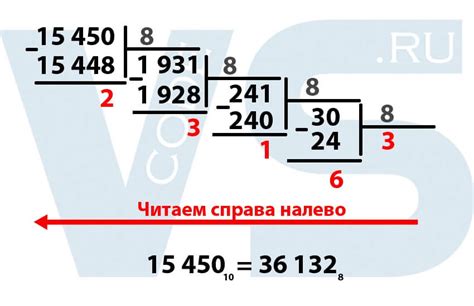
Как преобразовать число из десятичной системы в восьмеричную?
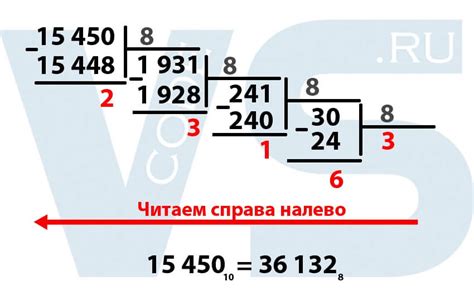
Преобразование числа из десятичной системы счисления в восьмеричную возможно с использованием простого алгоритма. Для этого достаточно разделить исходное число на 8 и записать остаток от деления в конечную восьмеричную запись числа. Затем повторять процесс, деля полученное частное на 8 и записывая остатки, пока оно не станет равным нулю.
Приведем пример преобразования числа 42 из десятичной системы в восьмеричную:
Шаг 1:
42 ÷ 8 = 5, остаток 2
Шаг 2:
5 ÷ 8 = 0, остаток 5
Теперь пишем остатки в обратном порядке и получаем восьмеричное представление числа 42 - 52.
Таким образом, любое число может быть преобразовано из десятичной системы в восьмеричную, следуя этому алгоритму. Этот метод основан на использовании деления с остатком и позволяет переводить числа из одной системы счисления в другую.
Примеры преобразования чисел из восьмеричной системы в десятичную

- Умножь каждую цифру числа в восьмеричной системе на 8 в степени, соответствующей позиции этой цифры.
- >Сложи полученные произведения.
Примеры:
| Восьмеричное число | Преобразование в десятичную систему |
|---|---|
| 12 | (1 * 8^1) + (2 * 8^0) = 10 |
| 53 | (5 * 8^1) + (3 * 8^0) = 43 |
| 777 | (7 * 8^2) + (7 * 8^1) + (7 * 8^0) = 511 |
Используя этот алгоритм, можно легко преобразовывать числа из восьмеричной системы в десятичную и наоборот.
Примеры преобразования чисел из десятичной системы в восьмеричную
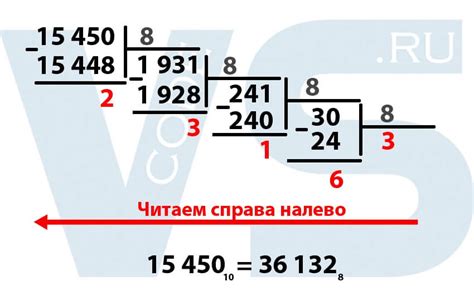
Преобразование числа из десятичной системы счисления в восьмеричную осуществляется путем деления числа на 8 и записи остатков в обратном порядке. Рассмотрим несколько примеров:
Пример 1:
Десятичное число: 25
Шаг 1: 25 / 8 = 3 (остаток 1)
Шаг 2: 3 / 8 = 0 (остаток 3)
Результат: Восьмеричное число 31
Пример 2:
Десятичное число: 100
Шаг 1: 100 / 8 = 12 (остаток 4)
Шаг 2: 12 / 8 = 1 (остаток 4)
Шаг 3: 1 / 8 = 0 (остаток 1)
Результат: Восьмеричное число 144
Пример 3:
Десятичное число: 987
Шаг 1: 987 / 8 = 123 (остаток 3)
Шаг 2: 123 / 8 = 15 (остаток 3)
Шаг 3: 15 / 8 = 1 (остаток 7)
Шаг 4: 1 / 8 = 0 (остаток 1)
Результат: Восьмеричное число 1733
Таким образом, мы видим, что для преобразования чисел из десятичной системы в восьмеричную достаточно последовательно делить число на 8 и записывать остатки. Полученные остатки, прочитанные в обратном порядке, составляют восьмеричное число.



