Ось симметрии отрезка порождает интересную и важную тему для изучения в 3 классе. Она позволяет нам представить себе отрезок, который является зеркальным отражением самого себя относительно некоторой линии. Это означает, что если мы сложим отрезок на свою ось симметрии, то получим такую же фигуру, но с точками отраженными относительно этой оси.
Определение оси симметрии отрезка может быть дано следующим образом: это прямая линия, которая делит отрезок на две равные части, так что каждая половина является зеркальным отражением другой.
Пример понимания оси симметрии отрезка может быть проиллюстрирован рассмотрением прямоугольника. Если мы нарисуем прямоугольник на листе бумаги и проведем ось симметрии относительно его, то получим две половинки этого прямоугольника, которые идентичны друг другу. Это позволяет нам восстановить прямоугольник, зная только половину его формы. Таким образом, ось симметрии помогает нам видеть симметричные фигуры и образовывать их с использованием зеркального отражения.
Что такое ось симметрии отрезка?
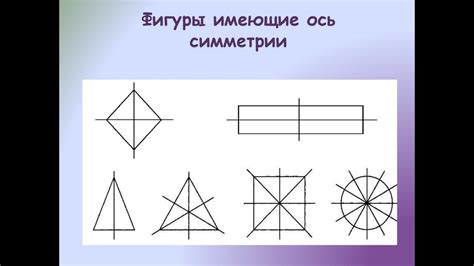
Отрезок имеет одну ось симметрии, которая является перпендикулярной самому отрезку и проходит через его середину. Это означает, что отрезок можно сложить вдоль оси симметрии, и полученные части будут полностью совпадать.
Например:
Ось симметрии на отрезке длиной 10 см будет проходить через его середину, на расстоянии 5 см от каждого конца. Если отрезок сложить вдоль оси симметрии, то правая и левая части будут полностью совпадать.
Определение и основные понятия

Для того чтобы найти ось симметрии отрезка, необходимо провести прямую линию, которая проходит через середину отрезка и перпендикулярна его направлению. Эта линия будет являться осью симметрии.
Ось симметрии отрезка имеет несколько основных свойств:
1. Симметрия:
Ось симметрии разделяет отрезок пополам, то есть левая и правая части отрезка являются существенно идентичными, симметричными относительно оси.
2. Равенство:
Левая и правая части отрезка, разделенного осью симметрии, имеют одинаковую длину и форму.
3. Отражение:
Если отразить одну часть относительно оси симметрии, получится другая часть абсолютно идентичной формы и размера.
Понимание основных понятий и определения оси симметрии отрезка поможет ученикам лучше понять геометрические принципы и улучшит их навыки в решении задач и конструировании фигур.
Способы определения оси симметрии отрезка
1. Геометрический способ. Для определения оси симметрии отрезка можно провести его серединную перпендикулярную линию. Это перпендикуляр, проходящий через середину отрезка и делящий его на две равные части. Ось симметрии будет проходить по этой серединной перпендикулярной линии.
2. Аналитический способ. Если известны координаты концов отрезка, то можно воспользоваться формулой для нахождения середины отрезка (xсер = (x1 + x2)/2, yсер = (y1 + y2)/2) и формулой для нахождения уравнения прямой, проходящей через две заданные точки. Уравнение этой прямой определяет ось симметрии отрезка.
3. Визуальный способ. Ось симметрии отрезка может быть определена визуально, если отрезок имеет явно выраженную симметричную форму. Например, отрезок между двумя точками, симметричными относительно вертикальной оси, будет иметь ось симметрии, совпадающую с этой вертикальной осью.
Определение оси симметрии отрезка позволяет лучше понять его свойства и структуру, а также использовать эти знания в решении геометрических задач.
Примеры оси симметрии отрезка
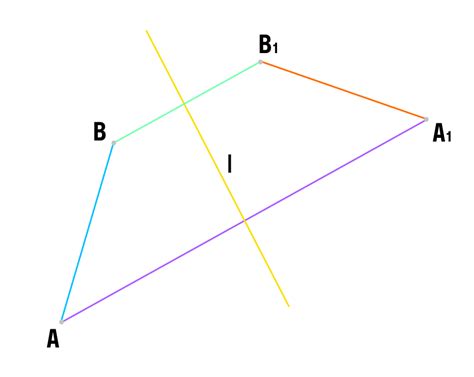
Пример 1:
Рассмотрим отрезок AB длиной 6 см. Ось симметрии отрезка может проходить по середине отрезка (то есть на расстоянии 3 см от точки A и точки B).
_________ A _________ B _________
_________ 3 см _________ 3 см _________
Пример 2:
Предположим, что отрезок CD длиной 8 см может иметь оси симметрии не только по центру, но и в других точках, например на расстоянии 2 см от точки C и 6 см от точки D:
_________ C _________ D _________
_________ 2 см _________ 2 см _________
_________ 2 см _________ 2 см _________
_________ 2 см _________ 2 см _________
_________ 6 см _________ 6 см _________
Пример 3:
Иногда ось симметрии отрезка может проходить не только по самому отрезку, но и через его продолжение. Например, рассмотрим отрезок EF длиной 5 см:
_________ E O _________
_________ 5 см • _________
Ось симметрии отрезка EF проходит через точку O, которая находится на расстоянии 2,5 см от точки E и на таком же расстоянии от точки F.
Это всего лишь примеры осей симметрии отрезка. Возможно много других вариантов осей, в зависимости от положения и длины отрезка.
Значимость оси симметрии отрезка в геометрии
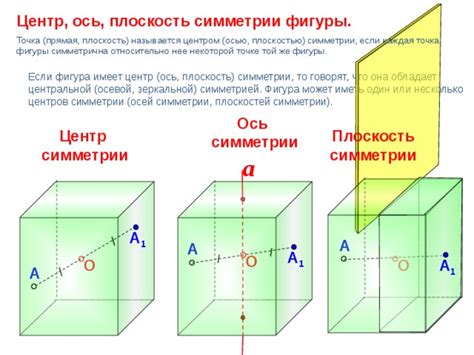
Ось симметрии отрезка – это воображаемая линия, которая делит данный отрезок на две равные части, таким образом, что отражая каждую точку первой части относительно этой оси, мы получим точку, совпадающую с соответствующей точкой второй части отрезка.
Знание о существовании оси симметрии отрезка дает нам не только визуальное представление о его симметричности, но и возможность дальнейшего изучения этих свойств в геометрии. Зная ось симметрии, мы можем узнать, как отразить каждую точку одной части отрезка относительно этой оси, чтобы она совпала с точкой другой части.
Ось симметрии отрезка важна при решении задач геометрии, позволяя нам определить точки симметрии на отрезке и использовать их для построения фигур или нахождения нужных значений.
Например: при построении симметричного отрезка относительно заданного отрезка, знание оси симметрии помогает нам точно определить положение точек симметрии и построить нужную фигуру.
Таким образом, понимание и использование оси симметрии отрезка играет важную роль в геометрии, позволяя нам анализировать и использовать симметричность относительно данного отрезка в различных геометрических задачах.
Математические выкладки и рассчеты для нахождения оси симметрии
Ось симметрии отрезка можно определить математическими выкладками и рассчетами. Процесс нахождения оси симметрии может быть разделен на несколько шагов.
1. Задается отрезок, для которого нужно найти ось симметрии.
2. Вычисляется длина отрезка. Для этого находится разница между координатами концов отрезка по оси X или Y, в зависимости от направления симметрии.
3. Длина отрезка делится на 2, чтобы найти середину отрезка. Это будет координата оси симметрии.
4. Ось симметрии отображается в виде прямой или точки на графике отрезка.
5. Проверяется, выполняется ли условие симметрии. Для этого выбираются точки с обоих концов отрезка и находится их симметричное расположение относительно оси симметрии.
6. Если все точки симметричны относительно оси, то она является осью симметрии отрезка. Если не все точки симметричны, то ось симметрии не существует.
Математические выкладки и рассчеты позволяют точно определить ось симметрии отрезка и проверить его симметричность. Этот метод может быть использован для любого отрезка, независимо от его длины и формы.



