Ортогональная проекция - это способ изображения трехмерных объектов на двумерной плоскости. Этот метод находит широкое применение в различных областях, таких как архитектура, графика и инженерное дело. Иногда также называют проекцией на плоскость.
Главной особенностью ортогональной проекции является то, что она сохраняет форму и размеры объекта, просто перенося его на плоскость. В этом случае применяются прямые или перпендикулярные линии, называемые линиями проекции. Такая проекция позволяет визуализировать трехмерный объект в двухмерном пространстве, что делает его более понятным и удобным для анализа и изучения.
Для выполнения ортогональной проекции требуется определенный набор правил и техник. Сначала выбирается плоскость проекции, которая может быть параллельна одной из координатных плоскостей, например, XY, XZ или YZ. Затем фигура проецируется на эту плоскость с использованием перпендикулярных или параллельных линий.
Понятие ортогональной проекции

При ортогональной проекции фигура располагается параллельно плоскости проекции, а прямые, соединяющие точки фигуры с соответствующими точками проекции, перпендикулярны этой плоскости.
Ортогональная проекция используется для удобного изображения объектов, в том числе архитектурных построек, деталей машин, графических моделей и других сложных фигур.
Пример:
Рассмотрим куб. Если мы хотим изобразить его на плоскости, мы можем использовать ортогональную проекцию. Для этого разместим куб параллельно плоскости проекции и проведем перпендикулярные линии от каждой точки куба до этой плоскости. Таким образом, мы получим двумерное изображение куба.
Что такое ортогональная проекция фигуры на плоскость

Ортогональная проекция основана на принципе параллельного проектирования лучей с фигуры на плоскость. При этом, проекционная плоскость должна быть перпендикулярна к оси обзора или плоскости, на которой лежит фигура. Такую проекционную плоскость называют также плоскостью проекции.
При ортогональной проекции все параллельные линии в трехмерном пространстве отображаются на параллельные линии на плоскости проекции. Это позволяет сохранить пропорции и формы объекта.
Для создания ортогональной проекции фигуры на плоскость используются различные виды проекций, такие как фронтальная проекция, горизонтальная проекция и плановая проекция. Каждая из проекций предоставляет определенный угол обзора и информацию о разных аспектах фигуры.
Ортогональная проекция фигуры на плоскость является важным инструментом при создании различных графических изображений и схем, а также при проектировании и строительстве зданий и сооружений. Она позволяет легко представить и анализировать различные аспекты объектов в двухмерном представлении, что упрощает восприятие и работу с информацией.
Как произвести ортогональную проекцию
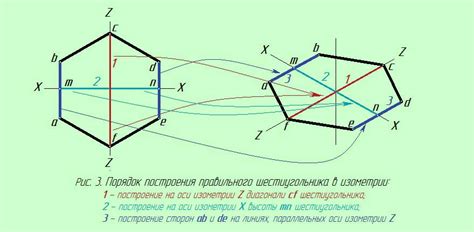
1. Выберите плоскость проекции. Это может быть любая плоскость, но обычно используется плоскость, перпендикулярная одной из осей координат.
2. Определите направление проекции. Выберите направление, в котором будут проецироваться точки фигуры на плоскость. Обычно это ось, параллельная плоскости проекции.
3. Проведите линии проекции. Проецируйте каждую точку фигуры на плоскость, соединяя их с точкой пересечения плоскости проекции и направления проекции.
4. Обозначьте полученные проекции. Каждая проекция будет представлять собой точку на плоскости проекции.
5. Постройте проекцию фигуры на плоскости. После того, как все точки фигуры будут проецированы на плоскость, соедините их линиями так, чтобы получился образ фигуры на плоскости.
Эти шаги помогут вам произвести ортогональную проекцию фигуры на плоскость. Практическое применение ортогональной проекции может быть найдено в архитектуре, инженерии, графике и других областях, где требуется изображение трехмерных объектов на плоскости.
Шаги выполнения ортогональной проекции
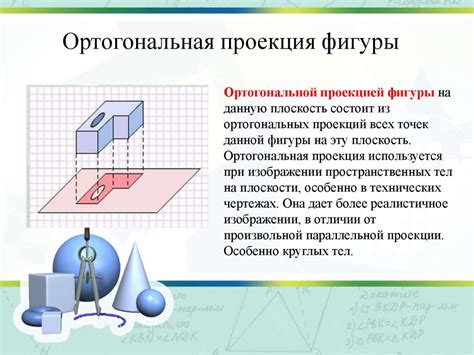
Для выполнения ортогональной проекции фигуры на плоскость необходимо следовать определенным шагам:
| Шаг 1: | Выбрать фигуру, которую нужно проецировать, и плоскость, на которую будет осуществляться проекция. |
| Шаг 2: | Найти точку проекции, которая будет являться основной точкой отсчета для проекционных линий. |
| Шаг 3: | Провести проекционные линии из точек фигуры к плоскости, проходящие через точку проекции. |
| Шаг 4: | Отметить точки пересечения проекционных линий с плоскостью. |
| Шаг 5: | Соединить полученные точки на плоскости линиями, чтобы получить проекцию фигуры. |
Таким образом, выполнение ортогональной проекции фигуры на плоскость включает последовательные действия выбора фигуры и плоскости, определение точки проекции, проведение проекционных линий и соединение точек на плоскости.
Инструменты для проведения ортогональной проекции
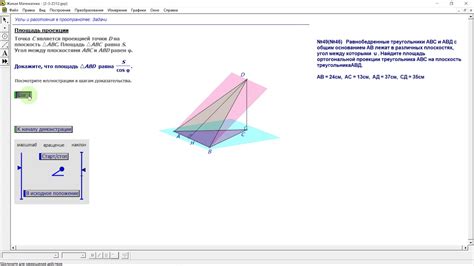
Для проведения ортогональной проекции фигуры на плоскость можно использовать различные инструменты и методы. Вот некоторые из них:
1. Геометрический компас
Геометрический компас является одним из основных инструментов для проведения ортогональной проекции. С его помощью можно точно определить и отметить точки на фигуре, которые необходимы для дальнейшего построения проекции.
2. Линейка
Линейка используется для проведения прямых линий при построении ортогональной проекции. Она помогает создать параллели и перпендикуляры, необходимые для правильного изображения фигуры на плоскости.
3. Карандаш и ручка
Карандаш и ручка служат для нанесения отметок и рисунков на фигуре в процессе проведения ортогональной проекции. Они помогают создать четкое и наглядное изображение фигуры на плоскости.
4. Уровень
Уровень используется для проверки горизонтальности и вертикальности линий при проведении ортогональной проекции. Он помогает достичь точности и точного пропорционального изображения фигуры.
5. Компьютерные программы
Современные компьютерные программы, такие как AutoCAD и SolidWorks, предоставляют возможность проводить ортогональную проекцию фигур на плоскость с высокой точностью и скоростью. Они используются в инженерии, архитектуре и других отраслях, где необходимо проводить проекции.
Важно понимать, что выбор инструментов для проведения ортогональной проекции зависит от задачи, требований к точности и индивидуальных предпочтений. Комбинация различных инструментов и методов может дать наилучший результат при построении ортогональной проекции фигуры на плоскость.
Примеры ортогональной проекции
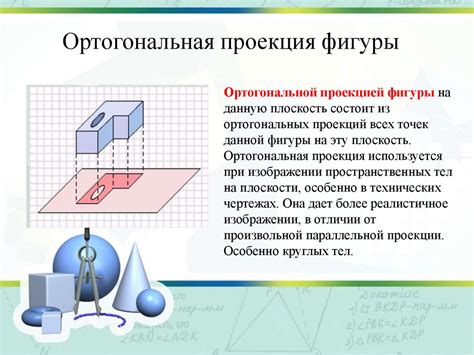
Ортогональная проекция широко используется в геометрии для представления трехмерных фигур в двумерном виде. Вот несколько примеров ортогональной проекции:
- Проекция точки на ось координат: если у нас есть точка P(x, y, z) в трехмерном пространстве, мы можем найти ее проекцию на плоскость, перпендикулярную оси z. В результате получим точку P(x, y, 0), которая будет являться проекцией точки на плоскость.
- Проекция отрезка на плоскость: если у нас есть отрезок AB в трехмерном пространстве, мы можем найти его проекцию на плоскость, перпендикулярную оси z. Для этого необходимо найти проекции конечных точек отрезка на плоскость и соединить их прямой.
- Проекция поверхности на плоскость: если у нас есть трехмерная поверхность, мы можем найти ее проекцию на плоскость, перпендикулярную оси z. Для этого необходимо найти проекции всех точек поверхности на плоскость и соединить их линиями.
- Проекция объемной фигуры на плоскость: если у нас есть объемная фигура, мы можем найти ее проекцию на плоскость путем нахождения проекций всех точек фигуры на плоскость и соединения их линиями или поверхностями.
Ортогональная проекция позволяет упростить изображение трехмерных объектов, делая их более понятными и легко воспринимаемыми. Она широко применяется в архитектуре, инженерии, компьютерной графике и других областях, где требуется работа с трехмерными моделями.



