В геометрии, точка - это одномерный объект, который не имеет длины, ширины или высоты. Точка обычно обозначается заглавной буквой латинского алфавита. Она является основным строительным блоком для конструирования фигур и решения геометрических задач.
Точка не имеет размеров, но она имеет определенные свойства. Одно из главных свойств точки - это ее положение в пространстве. Точка может находиться внутри фигуры, на границе фигуры или снаружи фигуры. Это свойство точки определяет ее принадлежность к определенной области и позволяет решать задачи, связанные с построением и определением геометрических объектов.
Еще одно важное свойство точки - это ее координаты. Координаты точки определяют ее положение относительно системы координат, которая вводится на плоскости или в пространстве. На плоскости точка определяется двумя координатами - абсциссой и ординатой. В трехмерном пространстве точка определяется тремя координатами - абсциссой, ординатой и аппликатой. Зная координаты точки, можно определить ее положение относительно других точек и фигур, а также вычислить расстояние между точками и угол между векторами.
Определение точки и ее роль в геометрии
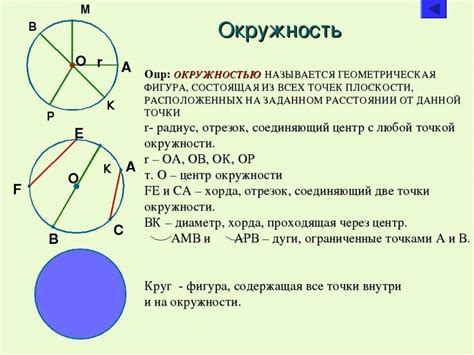
Точка обозначается обычно заглавной латинской буквой. Например, точку A или точку B.
Точка является фундаментальным элементом геометрии и имеет ряд важных свойств:
- Точка не имеет размеров: она не имеет ни длины, ни ширины, ни высоты. Она представляет собой математическую идею или концепцию.
- Точка не имеет направления: она не может быть направленной или повернутой. Точка не имеет ориентации в пространстве.
- Точка может быть определена двумя координатами: в декартовой системе координат точка может быть задана своими координатами (x, y).
- Точка может быть соединена с другими точками: две или более точки могут быть соединены прямой линией или отрезком. Это позволяет строить геометрические фигуры и определять отношения между точками.
Исследование точек и их свойств является основой для изучения различных геометрических объектов и фигур, таких как прямые, отрезки, окружности, многоугольники и т.д. Понимание понятия точки позволяет анализировать пространственные отношения и решать геометрические задачи.
Свойства точки в системе координат
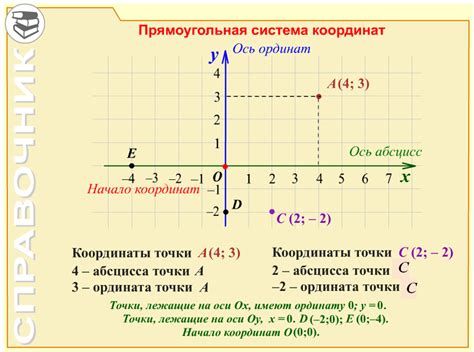
Точка в системе координат представляет собой абстрактный объект без размеров, который описывает положение объекта в пространстве.
У точки есть несколько важных свойств:
- Координаты: каждая точка в системе координат имеет две координаты - x и y. Координаты точки позволяют определить ее положение относительно начала координат.
- Расстояние до начала координат: расстояние от точки до начала координат можно вычислить с помощью теоремы Пифагора. Для точки с координатами (x, y) расстояние до начала координат равно квадратному корню из x^2 + y^2.
- Симметрия: точка с координатами (-x, -y) является симметричной к данной точке относительно начала координат.
Точки в системе координат широко используются в геометрии, физике, и других науках для описания положения и движения объектов. Они также играют важную роль в математических расчетах и графическом представлении данных.
Основные элементы геометрической точки
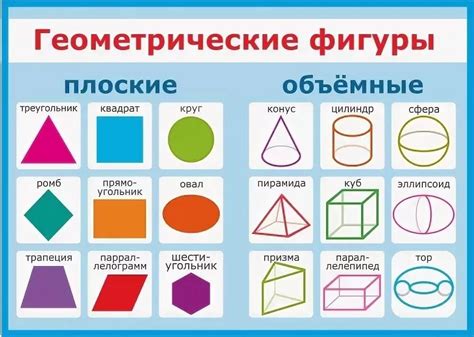
Свойства точки:
- Местоположение: Точка не имеет размеров и может быть расположена в пространстве в любом месте. Она может быть на горизонтали, вертикали или на плоскости.
- Идентичность: Каждая точка является уникальной и не может быть полностью совпадающей с другой точкой. Даже если точки находятся очень близко друг к другу, они все равно имеют свое собственное местоположение.
- Отношения: Точки могут быть связаны между собой различными отношениями. Например, можно провести прямую через две точки, соединить их отрезком или построить окружность с центром в точке.
- Координаты: Для удобства определения положения точки на плоскости или в пространстве используются координаты. В двумерном пространстве точка задается двумя числами - абсциссой (x) и ординатой (y), а в трехмерном пространстве - тремя числами - абсциссой (x), ординатой (y) и аппликатой (z).
Геометрическая точка является основой для построения других геометрических фигур и объектов. Она используется для определения прямых, отрезков, плоскостей, углов и т. д. Понимание основных свойств и элементов точки позволяет углубить знания о геометрии и применять их на практике.
Понятие расстояния между точками и его вычисление

В геометрии расстояние между двумя точками определяется как длина отрезка, соединяющего эти точки. Расстояние между точками может быть вычислено с помощью формулы, которая основана на теореме Пифагора.
Для вычисления расстояния между двумя точками A(x1, y1) и B(x2, y2) на плоскости используется формула:
d = √((x2 - x1)² + (y2 - y1)²)
где d - расстояние между точками A и B, x1 и y1 - координаты точки A, x2 и y2 - координаты точки B.
Данная формула основана на теореме Пифагора для прямоугольного треугольника, образованного отрезком, соединяющим точки A и B, и осями координат.
Таким образом, для вычисления расстояния между двумя точками на плоскости необходимо знать их координаты и воспользоваться формулой.
Точка как базовый элемент в фигурах и конструкциях
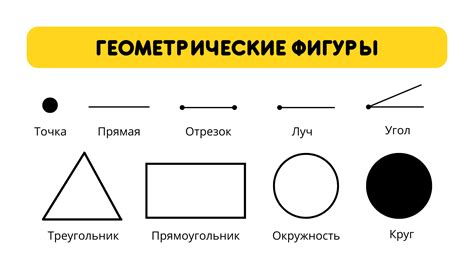
Точка может быть описана с помощью ее координат на плоскости. На плоскости каждая точка имеет две координаты - абсциссу (x) и ординату (y). Координатная ось x пересекает координатную ось y в точке, называемой началом координат или точкой О. Эта точка имеет координаты (0, 0) и служит нулевой точкой для определения координат других точек.
Точки можно соединять прямыми линиями, которые называются отрезками. Отрезки могут быть горизонтальными, вертикальными или наклонными. Если отрезок имеет концевую точку и начальную точку, то его можно представить в виде отрезка прямой, который соединяет две точки.
| Тип отрезка | Пример |
|---|---|
| Горизонтальный отрезок |  |
| Вертикальный отрезок |  |
| Наклонный отрезок |  |
Точки также используются для определения других фигур, таких как линии, окружности, треугольники, прямоугольники и многоугольники. Линия - это фигура, состоящая из бесконечного числа точек, расположенных вдоль одной линии. Окружность - это фигура, состоящая из всех точек на определенном расстоянии (радиусе) от данной точки, называемой центром окружности. Треугольник - это фигура, состоящая из трех отрезков, соединяющих три точки. Прямоугольник - это фигура, состоящая из четырех прямых отрезков, образующих прямые углы между собой.



