Диагональ – это отрезок, соединяющий две вершины многоугольника, не являющиеся соседними. В четырехугольнике, также известном как квадрат, диагонали играют важную роль и представляют собой особый элемент фигуры.
Квадрат – это четырехугольник, у которого все стороны равны друг другу и все углы равны 90 градусов. Вне зависимости от размеров и формы квадрата, его диагонали будут обладать определенными свойствами.
Первое свойство – диагонали квадрата равны друг другу. Это значит, что отрезок, соединяющий две противоположные вершины квадрата, имеет такую же длину, как и отрезок, соединяющий две другие противоположные вершины. Таким образом, диагонали квадрата являются равными сторонами прямоугольного треугольника.
Диагонали в четырехугольнике: основные принципы и свойства
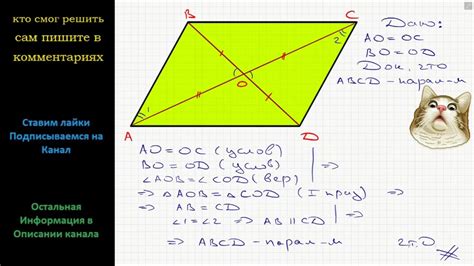
В четырехугольниках существует несколько основных свойств, связанных с диагоналями. Например, в выпуклом четырехугольнике сумма длин всех диагоналей равна полусумме периметра многоугольника. Это очень полезное правило, которое помогает нам вычислить длину диагонали, если известны длины сторон четырехугольника.
Еще одно важное свойство диагоналей связано с их взаимным пересечением. Две диагонали называются пересекающимися, если они имеют общую внутреннюю точку. При этом пересекающиеся диагонали делят четырехугольник на четыре треугольника. Заметим, что если диагонали равны между собой и пересекаются в точке, то четырехугольник является параллелограммом – фигурой с двумя парами параллельных сторон.
Другой интересный факт связан с диагоналями в равнобедренном трапеции. Диагональ, соединяющая основания трапеции, называется осью симметрии фигуры. Эта ось симметрии делит трапецию на две равные половины. Таким образом, диагонали в трапеции помогают раскрыть ее симметричность и выявить структурные особенности.
Диагонали в четырехугольнике представляют собой мощный инструмент для изучения и анализа свойств фигуры. Они помогают нам понять взаимосвязь между сторонами и углами, а также помогают выявить структурные и симметричные особенности четырехугольника. Изучение диагоналей играет важную роль в геометрии и поможет нам лучше понять мир окружающих нас фигур.
Отрезки, соединяющие вершины четырехугольника
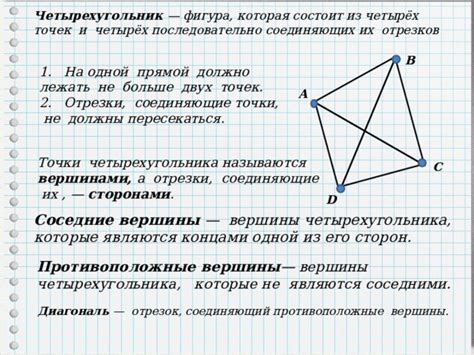
Диагонали делят четырехугольник на несколько треугольников. Количество таких треугольников зависит от количества вершин в четырехугольнике. Например, в четырехугольнике с вершинами A, B, C и D имеется две диагонали: AC и BD. Они делят четырехугольник на три треугольника: ABC, ACD и BCD.
Диагональ AC соединяет вершины A и C, а диагональ BD - вершины B и D. Каждая диагональ является отрезком прямой линии, который полностью лежит внутри четырехугольника.
Диагонали в четырехугольнике могут иметь разные свойства и выполнять различные функции. Например, некоторые диагонали могут быть равными по длине. Это значит, что отрезки, соединяющие определенные пары вершин, имеют одинаковую длину.
Диагонали также могут быть взаимно перпендикулярными. Это означает, что они пересекаются в прямом угле. Такое свойство диагоналей также имеет важное значение при решении геометрических задач и нахождении различных параметров четырехугольника.
Итак, диагонали в четырехугольнике - это отрезки, соединяющие вершины этой фигуры. Они имеют важную роль в структуре и свойствах четырехугольника и могут использоваться для решения геометрических задач.



