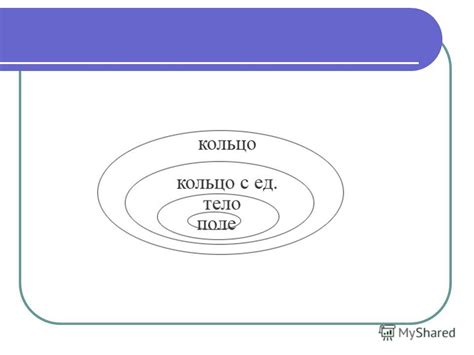
Кольцо - это алгебраическая структура, в которой определены операции сложения и умножения. Кольца широко применяются в различных областях математики, физики и информатики. Одно из самых известных примеров кольца - кольцо целых чисел.
В кольце должны выполняться следующие аксиомы:
- Закон коммутативности сложения: для любых элементов a и b из кольца a + b = b + a.
- Закон ассоциативности сложения: для любых элементов a, b и c из кольца (a + b) + c = a + (b + c).
- Существование нейтрального элемента по сложению: для любого элемента a из кольца существует элемент 0 такой, что a + 0 = 0 + a = a.
- Существование обратного элемента по сложению: для любого элемента a из кольца существует элемент -a такой, что a + (-a) = (-a) + a = 0.
- Закон коммутативности умножения: для любых элементов a и b из кольца a * b = b * a.
- Закон ассоциативности умножения: для любых элементов a, b и c из кольца (a * b) * c = a * (b * c).
- Дистрибутивность умножения относительно сложения: для любых элементов a, b и c из кольца a * (b + c) = a * b + a * c и (b + c) * a = b * a + c * a.
Если в кольце выполняется дополнительный закон ассоциативности умножения (то есть для любых элементов a, b и c из кольца (a * b) * c = a * (b * c)), то такое кольцо называется ассоциативным кольцом.
Поле - это кольцо, в котором для каждого ненулевого элемента существует обратный элемент по умножению. То есть для каждого элемента a из поля существует элемент 1/a такой, что a * (1/a) = (1/a) * a = 1. Примером поля является поле рациональных чисел.
Определение кольца

- Множество элементов должно быть замкнуто относительно операций сложения и умножения, то есть результат сложения или умножения двух элементов из множества также принадлежит этому множеству.
- Операция сложения должна быть ассоциативной, то есть для любых трех элементов a, b и c из множества верно равенство (a + b) + c = a + (b + c).
- В кольце должен существовать нулевой элемент, обозначаемый 0, такой что для любого элемента a из множества верно равенство 0 + a = a + 0 = a.
- Каждый элемент в кольце должен иметь противоположный элемент относительно сложения, то есть для каждого элемента a из множества должен существовать элемент b такой, что a + b = b + a = 0.
- Операция умножения также должна быть ассоциативной, то есть для любых трех элементов a, b и c из множества верно равенство (a * b) * c = a * (b * c).
- Должно выполняться свойство дистрибутивности умножения относительно сложения, то есть для любых трех элементов a, b и c из множества верно равенство a * (b + c) = (a * b) + (a * c) и (a + b) * c = (a * c) + (b * c).
Примеры кольцов включают множество целых чисел (Z), множество вещественных чисел (R) и множество комплексных чисел (C).
Кольцо в алгебре: общее понятие
- Множество элементов, обозначаемое как R, образует аддитивную абелеву группу с операцией сложения. Это означает, что сложение в кольце коммутативно, а также в нём существует нулевой элемент и к каждому элементу существует противоположный.
- Операция умножения в кольце ассоциативна и дистрибутивна относительно операции сложения. То есть, ассоциативность обеспечивает, что результат умножения не зависит от порядка выполнения операций, а дистрибутивность означает, что операция умножения распространяется на операцию сложения.
- В кольце существует единичный элемент, обозначаемый как 1, который удовлетворяет свойству a * 1 = 1 * a = a, где a - произвольный элемент кольца. Единичный элемент является нейтральным для умножения, то есть, умножение на него не меняет значение элемента.
Примерами кольца являются множество целых чисел (наиболее известное кольцо), множество вещественных чисел и множество матриц с операцией сложения и умножения.
Кольца могут быть различных типов, в зависимости от выполнения дополнительных свойств. Например, кольца могут быть коммутативными, если для умножения выполняется свойство коммутативности, или алгебраически замкнутыми, если в кольце любое уравнение имеет решение.
Кольца являются важным понятием в алгебре и находят применение в различных областях, включая линейную алгебру, теорию чисел и криптографию.
Свойства кольца и примеры
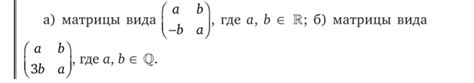
Кольцо, как алгебраическая структура, обладает рядом основных свойств:
| 1. Закон сложения | В кольце определена операция сложения, которая обладает свойствами ассоциативности, коммутативности и существования нулевого элемента. А именно, для любых элементов a, b и c из кольца, выполняется следующее равенство: a + (b + c) = (a + b) + c и a + b = b + a. Также существует элемент 0, такой что a + 0 = a для любого a из кольца. |
| 2. Закон умножения | В кольце определена операция умножения, которая обладает свойствами ассоциативности и дистрибутивности относительно сложения. А именно, для любых элементов a, b и c из кольца, выполняется следующее равенство: a * (b * c) = (a * b) * c и a * (b + c) = a * b + a * c. |
| 3. Существование нейтральных элементов | В кольце существуют нейтральные элементы относительно операций сложения и умножения. А именно, для любого элемента a из кольца существуют элементы 0 и 1, такие что a + 0 = a и a * 1 = a. |
| 4. Существование противоположных элементов | В кольце для каждого элемента a существуют противоположные элементы относительно операции сложения и обозначаются -a. А именно, a + (-a) = 0 и (-a) + a = 0. |
Некоторые примеры кольцов включают:
- Целочисленное кольцо: Множество целых чисел вместе с обычными операциями сложения и умножения образует кольцо.
- Кольцо вычетов по модулю: Множество вычетов по определенному модулю вместе с операциями сложения и умножения образует кольцо.
- Матричное кольцо: Множество матриц заданного размера вместе с операциями сложения и умножения матриц образует кольцо.
Это только некоторые примеры кольцов, которые используются в алгебре. Кольца играют важную роль в алгебре и имеют широкое применение в различных областях математики и физики.
Определение поля
Множество элементов поля должно удовлетворять следующим условиям:
- Закон сложения: для любых элементов a и b из поля, сумма a + b также является элементом поля.
- Закон умножения: для любых элементов a и b из поля, произведение a * b также является элементом поля.
- Законы коммутативности: операции сложения и умножения коммутативны, то есть для любых элементов a и b из поля, выполняются равенства a + b = b + a и a * b = b * a.
- Существование нейтральных элементов: существуют нейтральные элементы относительно сложения и умножения, которые обозначаются как 0 и 1 соответственно.
- Существование обратных элементов: для каждого ненулевого элемента a из поля существуют обратные элементы относительно сложения и умножения, которые обозначаются как -a и a-1 соответственно.
- Законы ассоциативности: операции сложения и умножения ассоциативны, то есть для любых элементов a, b и c из поля, выполняются равенства (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c).
- Распределительный закон: для любых элементов a, b и c из поля, выполняется равенство a * (b + c) = (a * b) + (a * c).
Примерами полей являются множества рациональных чисел, вещественных чисел и комплексных чисел. Поля играют важную роль в различных областях математики и имеют много применений в науке и технике.
Поле в алгебре: базовые понятия

Определение поля включает следующие основные понятия:
| Аксиомы сложения | Сложение в поле должно обладать свойствами коммутативности (a + b = b + a) и ассоциативности (a + (b + c) = (a + b) + c). Должен существовать нейтральный элемент 0, для которого a + 0 = a, а для каждого элемента a должен существовать противоположный элемент −a, такой что a + (−a) = 0. |
| Аксиомы умножения | Умножение в поле должно обладать свойствами коммутативности (a * b = b * a) и ассоциативности (a * (b * c) = (a * b) * c). Должен существовать нейтральный элемент 1, для которого a * 1 = a, а для каждого ненулевого элемента a должен существовать обратный элемент a^−1, такой что a * a^−1 = 1. |
| Распределительное свойство | Умножение в поле должно обладать свойством дистрибутивности относительно сложения: a * (b + c) = a * b + a * c. |
Примерами полей являются множества целых чисел, рациональных чисел и вещественных чисел с обычными операциями сложения и умножения.
Поля играют важную роль в алгебре, а также имеют множество приложений в различных областях науки, техники и других дисциплинах.
Свойства поля и примеры

| Свойство | Описание |
|---|---|
| Коммутативность сложения | a + b = b + a |
| Ассоциативность сложения | (a + b) + c = a + (b + c) |
| Существование нейтрального элемента по сложению | Существует элемент 0, такой что a + 0 = a |
| Существование обратного элемента по сложению | Для каждого элемента a существует элемент -a, такой что a + (-a) = 0 |
| Коммутативность умножения | a * b = b * a |
| Ассоциативность умножения | (a * b) * c = a * (b * c) |
| Существование нейтрального элемента по умножению | Существует элемент 1, такой что a * 1 = a |
| Существование обратного элемента по умножению | Для каждого ненулевого элемента a существует элемент 1/a, такой что a * (1/a) = 1 |
| Дистрибутивность умножения относительно сложения | a * (b + c) = (a * b) + (a * c) |
Примеры полей включают:
- Поле рациональных чисел Q, где сложение и умножение определены стандартным образом.
- Поле вещественных чисел R, которое включает все рациональные числа и их иррациональные числа, такие как корень из 2 или число \pi.
- Поле комплексных чисел C, которое включает в себя все вещественные числа и мнимую единицу i, такую что i^2 = -1.



