Геометрическое отображение - это процесс преобразования одной фигуры в другую с помощью определенных правил, сохраняющих некоторые свойства фигуры. В геометрии существуют различные типы геометрических отображений, такие как симметрия, сжатие, поворот и сдвиг.
Симметрия - это геометрическое отображение, при котором фигура сохраняется при отражении относительно прямой, называемой осью симметрии. Например, если мы отразим прямоугольник относительно его центральной вертикальной оси, то получим тот же самый прямоугольник, но в зеркальном отражении.
Сжатие - это геометрическое отображение, при котором все точки фигуры сжимаются или растягиваются вдоль определенной линии или относительно определенной точки. Например, если мы сжимаем круг, то он может стать эллипсом с большей осью, если мы растягиваем его вдоль оси OX.
Поворот - это геометрическое отображение, при котором фигура вращается вокруг определенной точки или оси на определенный угол. Например, если мы поворачиваем треугольник относительно точки O на 90 градусов против часовой стрелки, то получим новый треугольник, который будет выглядеть так, будто его вершины были повернуты на 90 градусов по часовой стрелке.
Сдвиг - это геометрическое отображение, при котором фигура сдвигается вдоль оси или вдоль прямой на определенное расстояние. Например, если мы сдвигаем прямоугольник вдоль оси OX на 5 единиц в положительном направлении, то получим новый прямоугольник, который будет смещен вправо на 5 единиц.
Определение геометрического отображения
Для примера, рассмотрим отображение точек на плоскости. Если каждой точке плоскости сопоставить ее отражение относительно заданной прямой, то получится отображение, которое сохраняет расстояния между точками (сохранение длин).
В геометрии для 7 класса существуют различные типы геометрических отображений, например, отражение, поворот и сдвиг. Они играют важную роль при исследовании свойств и особенностей геометрических фигур.
Понимание геометрических отображений помогает решать задачи, проводить конструкции и анализировать геометрические объекты.
Геометрическое отображение в геометрии для 7 класса

Параллельный перенос – это геометрическое отображение, при котором каждая точка фигуры смещается на одинаковое расстояние в определенном направлении. Например, если провести параллельный перенос четырехугольника вправо, каждая его точка переместится вправо на одно и то же расстояние.
Поворот – это геометрическое отображение, при котором фигура вращается вокруг заданной точки на определенный угол. Например, если повернуть треугольник на 90 градусов против часовой стрелки относительно его центра, его вершины поменяют местами и образуют новую фигуру.
Симметрия – это геометрическое отображение, при котором фигура отражается относительно заданной прямой, точки или плоскости. Например, если провести симметрию треугольника относительно его высоты, получится такой же треугольник, но с противоположной ориентацией.
Гомотетия – это геометрическое отображение, при котором фигура подобно исходной, но имеет другие размеры. Гомотетия определяется коэффициентом подобия, который указывает, во сколько раз увеличиваются (или уменьшаются) размеры фигуры. Например, если провести гомотетию треугольника с коэффициентом 2, его стороны увеличатся в два раза.
Геометрические отображения позволяют рассматривать геометрические фигуры как объекты, которые можно перемещать, поворачивать или изменять их размеры. Эти отображения помогают нам лучше понять геометрию и ее основные свойства.
Примеры геометрического отображения

1. Трансляция (сдвиг): это отображение, которое перемещает фигуру вдоль заданного направления. При трансляции все расстояния и углы между точками фигуры сохраняются.
2. Растяжение и сжатие: это отображение, которое изменяет размеры фигуры. Растяжение увеличивает все размеры фигуры в одинаковое число раз, в то время как сжатие уменьшает размеры фигуры.
3. Поворот: это отображение, которое вращает фигуру на заданный угол вокруг фиксированной точки. При повороте все расстояния и углы между точками фигуры сохраняются.
4. Отражение: это отображение, при котором фигура отражается относительно прямой, называемой осью отражения. Отраженная фигура похожа на оригинал, но зеркально отражена.
Это только некоторые из примеров геометрического отображения. В геометрии существует множество других типов отображений, каждое из которых имеет свои особенности и применение на практике.
Перемещение в плоскости
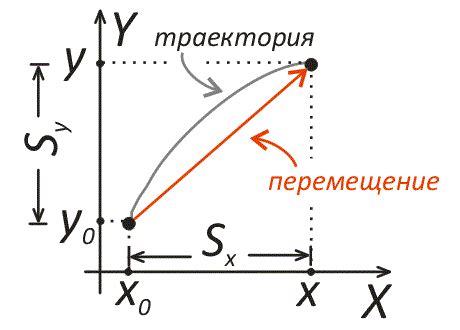
Перемещение задается двумя параметрами: вектором смещения и точкой, относительно которой происходит смещение. Вектор смещения - это направленный отрезок, длина которого равна расстоянию, на которое смещаются точки. При перемещении все точки плоскости смещаются параллельно по этому вектору.
Например, пусть дана точка с координатами (2, 3) и вектор смещения (4, -1). Чтобы переместить точку относительно этого вектора, нужно пройти 4 единицы по оси X в положительном направлении и 1 единицу по оси Y в отрицательном направлении. Итоговые координаты точки будут (6, 2).
Пример
Рассмотрим прямоугольник ABCD со сторонами AB = 4 и BC = 3, который находится в начале координат. Для перемещения прямоугольника вдоль оси X на 5 единиц в положительном направлении и вдоль оси Y на 2 единицы в отрицательном направлении, нужно переместить каждую точку прямоугольника соответственно. Так, AB сместится в точку A'B', где A'B' = AB + 5, а BC сместится в точку B'C', где B'C' = BC - 2. Получится прямоугольник A'B'C'D'.
Отражение относительно прямой
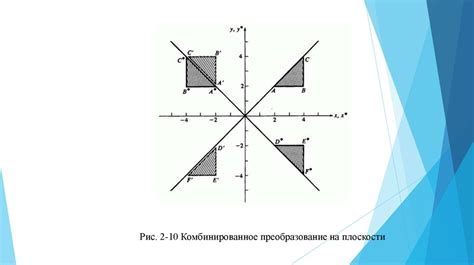
Для выполнения отражения относительно прямой можно использовать следующий алгоритм:
- Нарисуйте прямую отражения и точку, которую нужно отразить.
- Проведите перпендикуляр из точки до прямой.
- Измерьте расстояние от точки до прямой и откладывайте его от прямой, чтобы получить отраженную точку.
- Проведите прямую через исходную точку и отраженную точку.
- Исходная точка будет лежать на продолжении этой прямой.
Отражение относительно прямой имеет несколько свойств:
- Отображение сохраняет длины отрезков и углы между прямыми.
- Отображение меняет ориентацию фигуры на противоположную.
- Произведение коэффициентов наклона прямых до и после отражения равно -1.
Примером отражения относительно прямой может служить отбрасывание тени от объекта на поверхность. Тень отражается от поверхности, сохраняя форму и размеры объекта, но меняет его ориентацию.
Отражение относительно точки
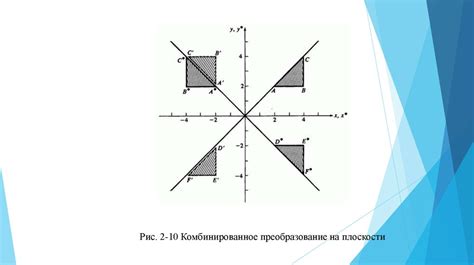
Для выполнения отражения относительно точки необходимо выполнить следующие шаги:
- Выберите точку, относительно которой будет выполняться отражение.
- Проведите линию, соединяющую выбранную точку с каждой точкой плоскости.
- На линиях, полученных на предыдущем шаге, отложите равные отрезки в противоположном отображении.
- Полученные точки являются отражением исходных точек относительно выбранной точки.
Пример:
Дана точка А(3,4) и точка О(0,0). Необходимо отразить точку А относительно точки О.
1. Выбираем точку О(0,0) в качестве центра отражения.
2. Проводим линию, соединяющую точку О с точкой А.
3. Откладываем на этой линии равные отрезки в противоположном отображении.
4. Получаем точку А' (-3,-4), которая является отражением точки А(3,4) относительно точки О(0,0).
Таким образом, отражение точки А(3,4) относительно точки О(0,0) равно точке А'(-3,-4).



