Описанная окружность в правильном многоугольнике - это окружность, которая проходит через все вершины многоугольника и является наибольшей окружностью, которую можно построить вокруг данного многоугольника.
Радиус описанной окружности может быть вычислен с использованием геометрических формул, зависящих от количества сторон в многоугольнике и от длины каждой стороны. Чем больше сторон у многоугольника, тем ближе радиус описанной окружности к его внешнему граничному радиусу. Радиус описанной окружности также связан с радиусом вписанной окружности и длиной сторон многоугольника.
Что такое описанная окружность в правильном многоугольнике?
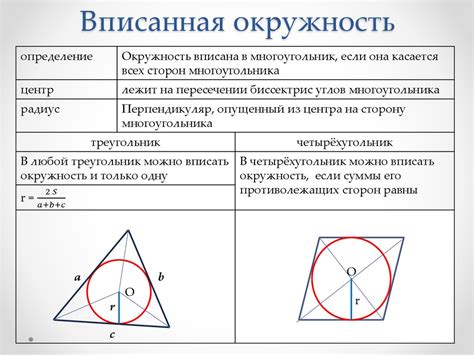
Окружность Эйлера в правильном многоугольнике имеет радиус, который может быть найден с использованием простой формулы. Радиус описанной окружности равен половине длины стороны многоугольника, деленной на синус угла между радиусом и половиной стороны.
Центр описанной окружности располагается в точке пересечения перпендикуляров, опущенных из середин каждой стороны многоугольника. Эта точка называется центром окружности.
Описанная окружность важна прежде всего для геометрических вычислений и наглядной демонстрации свойств и характеристик правильных многоугольников. Знание радиуса и центра окружности Эйлера позволяет решать задачи, связанные с многоугольниками, а также помогает в понимании их геометрических свойств.
Идея и определение

Для того чтобы найти радиус и центр описанной окружности в правильном многоугольнике, необходимо знать длину стороны многоугольника или его периметр. Кроме того, формула для вычисления радиуса и центра окружности в правильном многоугольнике зависит от количества сторон (вершин) многоугольника.
Существует несколько способов для вычисления радиуса и центра описанной окружности в правильном многоугольнике. Один из них - использование тригонометрических функций, таких как синус и косинус. Другой способ - использование геометрических свойств многоугольника, таких как равнобедренность треугольников и центральный угол.
Зная радиус и центр описанной окружности, можно решать различные задачи, связанные с многоугольником, такие как нахождение площади, периметра, углов и других характеристик.
| Количество сторон | Формула радиуса | Формула центра |
|---|---|---|
| 3 (равносторонний треугольник) | r = a / sqrt(3) | Центр совпадает с центром масс треугольника |
| 4 (квадрат) | r = a / 2 | Центр совпадает с центром масс квадрата |
| 5 (правильный пятиугольник) | r = a * sqrt((5 - sqrt(5)) / 10) | Центр - точка пересечения диагоналей |
| 6 (правильный шестиугольник) | r = a / 2 | Центр - точка пересечения диагоналей |
| n (правильный n-угольник) | r = (a / 2) * cot(π/n) | Центр - точка пересечения диагоналей |
Свойства и особенности описанной окружности
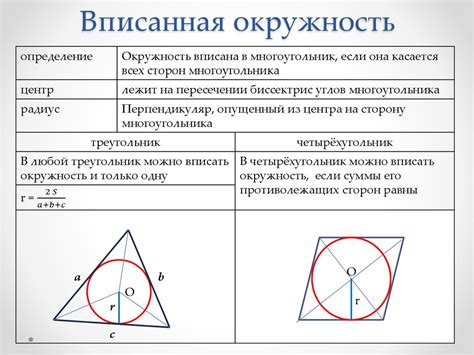
Описанная окружность имеет несколько особенностей и свойств, которые полезно знать:
- Центр окружности - это точка, лежащая на пересечении всех перпендикуляров, проведенных к сторонам многоугольника. Центр окружности равноудален от всех вершин многоугольника.
- Радиус окружности - это расстояние от центра окружности до любой вершины многоугольника.
- Теорема о радиусе окружности гласит, что радиус описанной окружности равен половине длины диагонали многоугольника.
- Касательная к описанной окружности ведет себя особенным образом. Она проходит через вершину многоугольника и перпендикулярна радиусу, проведенному в эту вершину.
- Диаметр окружности - наибольшее расстояние между двумя точками на окружности. В случае описанной окружности, диаметр равен двукратному радиусу.
Знание свойств описанной окружности позволяет упростить решение различных задач и находить различные параметры многоугольников, основанных на описанной окружности.
Как найти радиус описанной окружности?
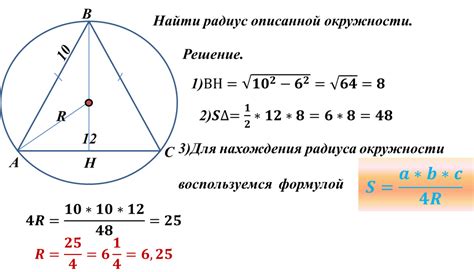
| Формулы радиуса описанной окружности: | |
|---|---|
| Радиус окружности: | R = a / (2 * sin(π/n)), |
| где a – длина стороны многоугольника, | |
| n – количество сторон многоугольника. |
Другой способ найти радиус описанной окружности – это используя формулу:
| Формула вписанной окружности: | |
|---|---|
| Радиус окружности: | R = a / (2 * tan(π/n)). |
Обратите внимание, что в обоих случаях результатом будет радиус окружности, описанной вокруг правильного многоугольника.
Способы нахождения координат центра окружности
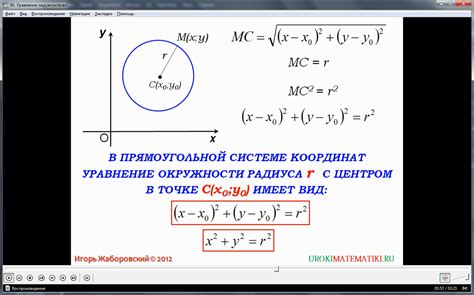
Способ 1: Для нахождения координат центра окружности в правильном многоугольнике можно использовать геометрический подход. В этом подходе мы знаем, что центр окружности лежит на пересечении биссектрис внутренних углов многоугольника. Для этого выбираем две произвольные стороны многоугольника и найденем их биссектрисы. Пересечение этих биссектрис и будет центром окружности.
Способ 2: Другой способ нахождения координат центра окружности заключается в использовании комплексных чисел. В этом способе каждая вершина многоугольника представляется в виде комплексного числа, где действительная часть соответствует оси OX, а мнимая - оси OY. Затем находим среднее арифметическое всех вершин многоугольника, и получаем координаты центра окружности.
Способ 3: Еще один способ нахождения координат центра окружности основан на применении trigonometry. Для этого вычисляются синусы и косинусы углов между центром многоугольника и его вершинами. Затем находится среднее арифметическое значений косинусов и синусов и получаем координаты центра окружности.
Выбор метода нахождения координат центра окружности зависит от доступных данных и предпочтений исследователя. Каждый из методов имеет свои преимущества и недостатки, и их выбор в конечном итоге определяется удобством и точностью вычислений.
Решение задачи описания окружности в правильном многоугольнике

Для начала, нам понадобится знать длину стороны многоугольника. Пусть S - это длина стороны, N - количество вершин многоугольника. Тогда радиус окружности можно вычислить по формуле:
Радиус = S / (2 * sin(π/N))
Центр окружности будет находиться в точке пересечения биссектрис всех углов многоугольника. Для правильного многоугольника это будет точка пересечения всех его диагоналей.
Итак, для решения задачи:
- Найдите длину стороны многоугольника.
- Вычислите радиус окружности по формуле.
- Постройте биссектрисы всех углов многоугольника и найдите точку их пересечения - это центр окружности.
Теперь вы знаете, что такое описанная окружность в правильном многоугольнике и как найти ее радиус и центр. Не забывайте применять эти знания при решении геометрических задач!
Полезные примеры и практические задачи

Описанная окружность в правильном многоугольнике имеет множество применений в геометрии и инженерии. Рассмотрим несколько полезных примеров и практических задач, связанных с этой темой.
Пример 1:
Пусть у нас есть правильный треугольник со стороной a. Чтобы найти радиус описанной окружности, можно воспользоваться следующей формулой:
r = a / (2 * sin(60°))
Где a - длина стороны треугольника, r - радиус описанной окружности.
Пример 2:
Допустим, у нас имеется правильный пятиугольник со стороной b. Чтобы найти радиус описанной окружности, можно использовать следующую формулу:
R = b / (2 * sin(36°))
Где b - длина стороны пятиугольника, R - радиус описанной окружности.
Практическая задача:
Пусть у нас есть вершины правильного семиугольника в трехмерном пространстве с координатами (x1, y1, z1), (x2, y2, z2) и (x3, y3, z3). Чтобы найти центр описанной окружности, можно воспользоваться следующей формулой:
xc = (x1 + x2 + x3) / 3
yc = (y1 + y2 + y3) / 3
zc = (z1 + z2 + z3) / 3
Где (xc, yc, zc) - координаты центра описанной окружности.
Это всего лишь несколько примеров использования описанной окружности в правильном многоугольнике. Зная радиус и центр окружности, можно решать разнообразные геометрические задачи, моделировать фигуры и создавать новые строения.



