Округление чисел является обычной задачей, которую приходится решать во многих сферах жизни. Его применение особенно важно, когда точность вычислений или представление данных имеют решающее значение. Одним из наиболее распространенных и полезных видов округления является округление до 3 значащих цифр.
Округление до 3 значащих цифр позволяет выразить число с максимально возможной точностью при сохранении практичности и удобства использования. Это особенно полезно в научных и инженерных расчетах, где точность является ключевым фактором. Округление до 3 значащих цифр позволяет избежать излишней детализации и облегчить восприятие результатов вычислений.
Правила округления до 3 значащих цифр достаточно просты. Если первая отбрасываемая цифра меньше 5, то следует оставить первые 3 цифры без изменений. Если первая отбрасываемая цифра больше или равна 5, то следует увеличить последнюю оставляемую цифру на единицу и отбросить все последующие цифры. Например, число 23.456 округляется до 23.5, а число 67.893 округляется до 67.9.
Округление чисел: важность и применение

Во-первых, округление чисел помогает при записи и представлении больших и маленьких чисел. Например, сложно и неудобно работать с числом 1234567890.123456789 в десятичной системе счисления, но если округлить его до 1.23e+09, становится гораздо проще и понятнее.
Во-вторых, округление чисел упрощает сравнение и анализ данных. Зачастую точность до двух или трех значащих цифр уже достаточна для получения нужной информации. Например, при анализе экономических показателей округление чисел позволяет быстро определить тренды и сравнить различные показатели.
В-третьих, округление чисел используется для представления результатов вычислений или измерений с определенной точностью. Например, в физике или инженерных расчетах округление чисел до определенного числа значащих цифр помогает учесть погрешности измерений и получить более точные и реалистичные результаты.
Однако, правила округления чисел могут различаться в зависимости от контекста и требований. Некоторые системы используют правила "вверх" или "вниз", где число округляется до ближайшего большего или меньшего числа. Другие системы могут использовать правила "к четному" или "отсечения", при которых число округляется до ближайшего четного числа или просто отбрасывается дробная часть.
Поэтому, при работе с округлением чисел важно всегда учитывать контекст и требования задачи, чтобы получить наиболее точные и правильные результаты.
Таким образом, округление чисел играет важную роль в различных областях науки и практического применения, облегчая работу с числовыми данными и обеспечивая точность и понятность результатов.
Выгоды округления чисел в повседневной жизни

Округление чисел до 3 значащих цифр имеет множество практических применений в повседневной жизни:
1. Финансы: Округление чисел – это один из способов упростить вычисления и снизить ошибки в финансовых операциях. Округляя суммы, множители или процентные ставки, мы легко считаем и делаем быстрые оценки своих расходов и доходов.
2. Математические модели: В научных и технических расчетах, особенно при использовании больших чисел или комплексных формул, округление чисел может помочь упростить моделирование и улучшить точность результатов.
4. Упрощение коммуникации: Округление чисел делает коммуникацию более ясной и понятной. Вместо сложных и нечетких десятичных дробей, мы можем использовать более простые и понятные целые числа или числа с несколькими десятичными знаками.
5. Улучшение дизайна и оформления: Округление чисел может сделать визуальные элементы, такие как диаграммы, графики и таблицы, более читабельными и привлекательными. Отображение чисел с меньшим количеством десятичных знаков может улучшить восприятие информации и упростить ее интерпретацию.
Округление чисел до 3 значащих цифр предлагает множество преимуществ и широко используется во многих сферах нашей повседневной жизни. Оно помогает улучшить точность вычислений, облегчить анализ данных и упростить коммуникацию. Понимание правил округления и его практических применений может быть полезным для нас всех.
Правила округления до трех значащих цифр
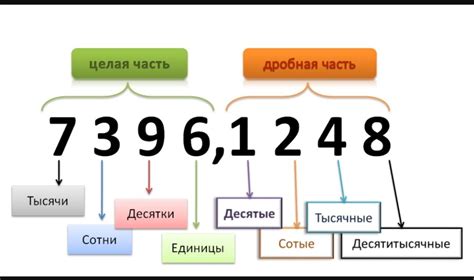
1. Если первая значащая цифра меньше 5, то все остальные цифры отбрасываются и число округляется в меньшую сторону. Например, число 3.14159 округляется до 3.14.
2. Если первая значащая цифра больше или равна 5, то она округляется в большую сторону, а остальные цифры отбрасываются. Например, число 6.75893 округляется до 6.76.
3. В случае, когда первая значащая цифра равна 5, округление происходит к ближайшему четному числу. Например, число 5.835 округляется до 5.84, а число 5.825 округляется до 5.82.
Правила округления до трех значащих цифр являются основными и широко применяются в научных и финансовых расчетах, а также в повседневной жизни. Они помогают упростить и уточнить результаты вычислений, делая их более удобными для использования.
Примеры округления чисел для наглядности
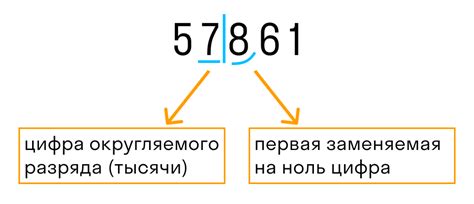
Округление чисел до 3 значащих цифр может использоваться в различных сферах, где требуется представление чисел более компактным и понятным образом. Рассмотрим несколько примеров округления чисел:
Пример 1: Рассмотрим число 1234.5678. Округление до 3 значащих цифр приведет к числу 1230. Это означает, что все числа после третьей значащей цифры (в случае данного числа - 4) будут отброшены, а третья значащая цифра будет округлена в сторону ближайшего целого числа. В данном случае, третья значащая цифра - 3, поэтому она округляется вверх до 4, а все остальные цифры отбрасываются.
Пример 2: Рассмотрим число 0.00056789. Округление до 3 значащих цифр приведет к числу 0.000568. В данном случае третья значащая цифра - 5, поэтому она округляется в сторону ближайшего целого числа. Цифры после третьей значащей цифры отбрасываются.
Пример 3: Рассмотрим число 987654. Округление до 3 значащих цифр приведет к числу 988000. В данном случае третья значащая цифра - 7, поэтому она округляется вверх до 8, а все остальные цифры становятся нулями.
Приведенные примеры показывают, как округление чисел до 3 значащих цифр может изменять представление чисел, делая их более компактными, но при этом сохраняя основную информацию.



