Числа - это одно из фундаментальных понятий в математике. С их помощью мы описываем мир, вычисляем, измеряем, прогнозируем. В математике существует несколько видов чисел, каждое из которых имеет свои особенности и связи с другими видами чисел.
Одним из таких видов чисел являются обратные числа. Обратным числом к данному числу называется такое число, произведение которого на данное число равно 1. Например, обратные числа к 2 и 1/2 равны 1/2 и 2 соответственно. Обратные числа имеют важное значение в различных областях науки и техники.
В то же время, противоположные числа являются понятием, обратным к понятию «число». Противоположным числом к данному числу называется число, которое находится на одинаковом расстоянии от нуля по числовой прямой, но с противоположным знаком. Например, противоположное число к 3 – это -3, а к -5 – это 5. Противоположные числа имеют свойства, позволяющие решать уравнения и выполнять различные операции в алгебре.
Различия между обратными и противоположными числами

Обратные числа представляют собой числа, в результате умножения которых на исходное число получается единица. Например, обратное число к двум будет равно 1/2, так как 2 * (1/2) = 1. Обратное число к нулю не существует, так как нельзя поделить на ноль.
Противоположные числа, с другой стороны, являются числами, которые находятся на разных сторонах от нуля на числовой прямой и, при сложении их значений, дают ноль. Например, противоположное число к 3 будет равно -3, так как 3 + (-3) = 0.
Главное различие между этими понятиями заключается в операции, которая используется. Обратные числа определяются через операцию умножения, а противоположные числа - через операцию сложения.
Также стоит отметить, что обратные числа применяются в различных областях математики, таких как алгебра, геометрия и физика, для решения уравнений и задач. Противоположные числа часто используются для определения относительных значений и направлений.
В общем, обратные и противоположные числа имеют свои уникальные свойства и применение, и их понимание является важным элементом в освоении основ математики.
Обратные числа и их свойства
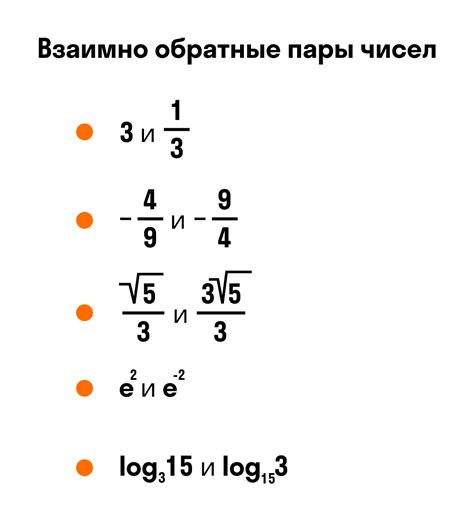
Свойства обратных чисел:
- Каждое число, кроме нуля, имеет обратное число.
- Обратное число для нуля не существует, так как деление на ноль неопределено.
- Сумма обратных чисел всегда равна нулю: a + (-a) = 0.
- Умножение обратного числа на само себя всегда дает единицу: a * (1/a) = 1.
Обратные числа широко используются в различных областях. Например, в математической физике они позволяют решать уравнения, связанные с движением и силами. В финансовой математике обратные числа помогают рассчитывать процентные ставки и валютные обмены.
Понимание обратных чисел является важным элементом математической грамотности и способствует развитию логического мышления. Знание и применение свойств обратных чисел позволяет более глубоко понять мир математики и его применение в реальной жизни.
Противоположные числа: определение и примеры
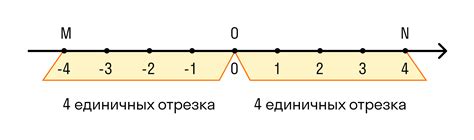
Например, числа 5 и -5 являются противоположными, так как их сумма равна нулю. Аналогично, 8 и -8, 13 и -13 – все эти пары чисел являются противоположными.
Противоположные числа используются в алгебре и математике для упрощения выражений и решения уравнений. Чтобы найти противоположное число данному, нужно поменять его знак на противоположный.
Важно помнить, что только действительные числа могут иметь противоположные значения, а нуль не имеет противоположного числа.
Связь между обратными и противоположными числами

Обратные числа - это числа, при умножении на которые получается единица. Например, обратным числом для 2 является 1/2, потому что 2 * (1/2) = 1. Обратные числа обладают свойством, что их произведение всегда равно единице.
Противоположные числа - это числа, которые имеют одинаковую абсолютную величину, но противоположный знак. Например, противоположное число для 5 -(-5), потому что 5 + (-5) = 0. Противоположные числа всегда складываются в ноль.
Связь между обратными и противоположными числами заключается в том, что обратное число противоположного числа равно самому числу. Например, обратное число для -3 это -1/3, потому что -3 * (-1/3) = 1. Это свойство позволяет использовать обратные числа вместо противоположных чисел при выполнении операций, таких как умножение и деление.
Использование обратных чисел и противоположных чисел позволяет упростить множество математических операций и вычислений. Они широко применяются в различных областях науки, инженерии и финансах для решения различных задач.
Практическое использование обратных и противоположных чисел
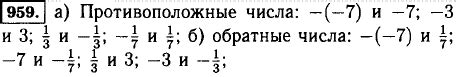
Обратные числа находят применение в различных областях математики и физики. Они позволяют описывать явления, обратные исходному, либо являющиеся противоположными.
Одним из примеров использования обратных чисел является решение уравнений. Если мы знаем, что при умножении двух чисел получается единица, то одно из них будет обратным к другому. Например, число 5 является обратным к 1/5, поскольку их произведение равно 1. Это помогает в решении уравнений, где требуется определить обратные значения для неизвестных.
Противоположные числа также находят свое применение в различных ситуациях. Они используются для описания разностей и противоположностей. Например, в математике противоположными числами являются пары чисел, сумма которых равна нулю. Такие числа называются антиподами. Например, -2 и 2 являются противоположными числами, поскольку их сумма равна нулю.
В физике противоположные числа используются для описания положительных и отрицательных зарядов, например, при описании электрических полей. Положительный и отрицательный заряды считаются противоположными, поскольку они имеют разные знаки и притягиваются друг к другу.
Таким образом, обратные и противоположные числа имеют важное практическое значение в различных областях науки и повседневной жизни. Их использование позволяет описывать явления, связанные с противоположностями, и решать разнообразные математические и физические задачи.



