В мире геометрии, прямые и параллельные плоскости являются основными понятиями, которые отражаются в разных сферах нашей жизни. Однако, существуют множество распространенных заблуждений и неверных утверждений, связанных с этими терминами. Часто люди сбиваются с пути, впадая в путаницу или просто не зная точного определения данных понятий.
Прямая – это линия, которая не имеет изгибов и сохраняет одинаковое направление на всем протяжении. Она состоит из бесконечного числа точек, отличается отрезком (конечным отрезком), которым связываются только две точки, а также от плоскости, которая располагается в трех измерениях.
Параллельные плоскости – это плоскости, которые никогда не пересекаются. Отличается одним из основных понятий геометрии, которое играет важную роль в математическом исследовании. Каждая пара параллельных плоскостей имеет определенное расстояние между ними, сохраняющееся при любых условиях.
Правила определения прямых и параллельных плоскостей
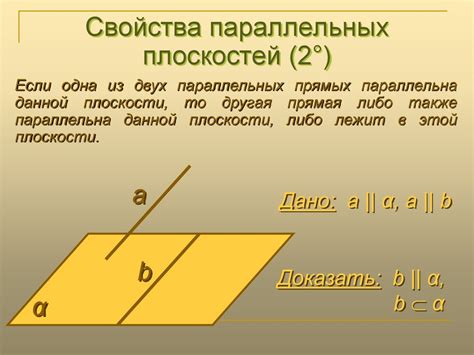
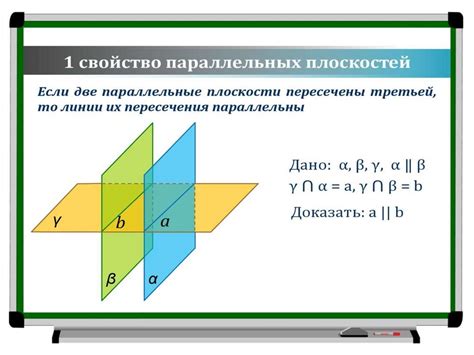
Правило 1: Две плоскости считаются параллельными, если они не пересекаются ни в одной точке и не лежат в одной плоскости.
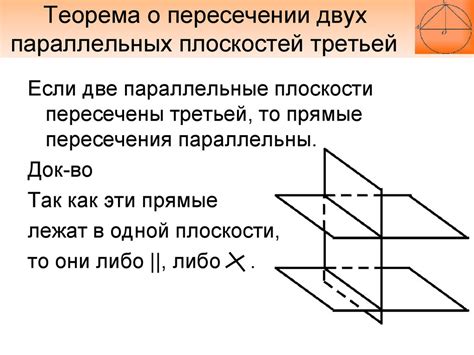
Правило 2: Две плоскости, лежащие в одной плоскости, считаются параллельными, если они имеют общую прямую линию.
Правило 3: Две прямые в пространстве считаются пересекающимися, если они имеют общую точку.
Правило 4: Две прямые считаются параллельными, если они не имеют общих точек и лежат в одной плоскости
Правило 5: Две прямые, не лежащие в одной плоскости, никогда не могут быть параллельными.
Знание этих правил позволяет определить взаимное расположение прямых и плоскостей в пространстве. Это может быть полезной информацией при решении геометрических задач или в практических задачах, связанных с построением и конструированием.
Последствия неверных утверждений о прямых и параллельных плоскостях
Неверные утверждения о свойствах прямых и параллельных плоскостей могут привести к серьезным ошибкам и непониманию при решении математических задач и проблем, а также в применении этих знаний в реальных ситуациях. Неправильное понимание и применение правил и свойств прямых и параллельных плоскостей может иметь следующие последствия:
1. Неверные вычисления и решения задач. Если в процессе решения задачи с заранее неверно заданными прямыми или плоскостями используется неправильная формула или алгоритм, то расчеты могут быть неверными, что может привести к неправильному результату и ошибке в ответе.
3. Неверное моделирование и проектирование. В области инженерии, архитектуры и других наук о строительстве и дизайне, неправильное представление о прямых и параллельных плоскостях может привести к неправильному моделированию и проектированию, что может иметь серьезные последствия в реальной жизни, включая разрушение строений или неэффективное использование ресурсов.
4. Возникновение противоречий и парадоксов. Неправильные утверждения о свойствах прямых и параллельных плоскостей могут противоречить другим математическим теоремам и приводить к логическим парадоксам, которые усложняют искомое решение задачи или делают его невозможным.
5. Потеря доверия к математике и наукам. Если неверные утверждения о прямых и параллельных плоскостях становятся повсеместными и принимаются как истина, это может вызывать сомнения в надежности и точности математических знаний и наук в целом. Это может привести к потере доверия к математике и уменьшению интереса к изучению предметов, связанных с этой областью знаний.
Математическое доказательство неправильности суждений о прямых и параллельных плоскостях

В математике существует ряд неверных утверждений о прямых и параллельных плоскостях, которые могут ввести в заблуждение и привести к неправильному решению задач. Для опровержения таких утверждений можно привести математическое доказательство на основе известных свойств и теорем.
Рассмотрим утверждение: "Если две прямые перпендикулярны к одной и той же плоскости, то они параллельны между собой". Это утверждение, на первый взгляд, кажется логичным и верным, однако оно является неверным.
Доказательство неправильности данного утверждения основывается на следующих фактах:
- Прямые, перпендикулярные к одной и той же плоскости, не обязательно лежат в одной плоскости.
- Параллельные прямые не обязательно перпендикулярны к одной и той же плоскости.
Таким образом, утверждение о параллельности прямых, перпендикулярных к одной плоскости, является неверным. Это доказывает, что при решении задач, связанных с прямыми и плоскостями, необходимо учитывать указанные факты и быть внимательным к постановке утверждений.
Распространенные ошибки в определении прямых и параллельных плоскостей

1. Путаница между параллельными и совпадающими прямыми
Одной из распространенных ошибок является путаница между параллельными и совпадающими прямыми. Параллельные прямые - это две прямые, которые никогда не пересекаются и всегда находятся на одной плоскости. Совпадающие прямые - это две прямые, которые совпадают и полностью совпадают друг с другом. Необходимо понимать, что параллельные прямые могут иметь одну общую точку, но не пересекаться, в то время как совпадающие прямые полностью сливаются в одну прямую.
2. Неправильное определение параллельных плоскостей
Еще одна распространенная ошибка связана с определением параллельных плоскостей. Параллельные плоскости - это две плоскости, которые никогда не пересекаются и всегда находятся на одном и том же расстоянии друг от друга. Ошибка заключается в том, что некоторые люди могут думать, что параллельные плоскости полностью совпадают, что неверно. Параллельные плоскости могут иметь общие точки, но они никогда не пересекаются и всегда остаются на постоянном расстоянии друг от друга.
3. Необходимость проверки углов
Одна из частых ошибок заключается в том, что люди считают, что прямые и плоскости, которые имеют одинаковые углы, являются параллельными. Однако это неверное утверждение, поскольку существуют различные конфигурации прямых и плоскостей, которые могут иметь одинаковые углы, но не являются параллельными. Для определения параллельных прямых и плоскостей необходимо проверить их взаимное расположение и отсутствие пересечений.
Итак, для правильного определения прямых и параллельных плоскостей важно помнить о различиях между параллельными и совпадающими прямыми, правильно определять параллельные плоскости и проверять углы для подтверждения параллельности. Избегая этих распространенных ошибок, можно гарантировать более точное понимание и применение этих концепций в геометрии.
Значение правильного определения прямых и параллельных плоскостей в геометрии
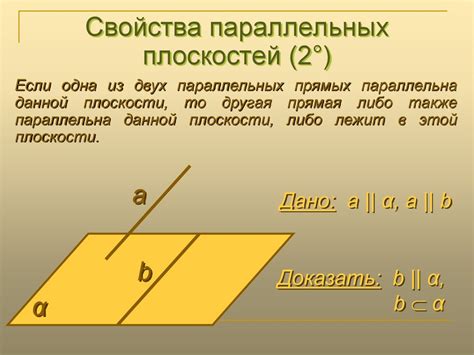
Прямая в геометрии - это линия, которая не имеет ни длины, ни ширины. Она обладает только направлением. Параллельные плоскости - это плоскости, которые не пересекаются и расположены на одинаковом расстоянии друг от друга на всей своей протяженности.
Правильное определение прямых и параллельных плоскостей позволяет изучать пространственные объекты и их взаимное расположение с большей точностью. Например, зная, что две плоскости параллельны, мы можем утверждать, что все прямые, лежащие в одной из этих плоскостей, будут параллельны прямым, лежащим в другой параллельной плоскости.
Также, зная, что две прямые перпендикулярны к одной и той же плоскости, мы можем утверждать, что они будут параллельны друг другу. Это можно использовать для решения задач на построение геометрических фигур или для определения взаимного положения объектов в пространстве.
В геометрии важно понимать смысл основных понятий и уметь их правильно определять, чтобы применять их в решении задач и построении геометрических фигур. Точное определение прямых и параллельных плоскостей является основой для дальнейшего изучения геометрии и применения ее результатов в различных областях науки и техники.
Возможности применения знания о прямых и параллельных плоскостях в реальной жизни

Строительство: Понимание прямых и параллельных плоскостей очень полезно в строительстве. Архитекторы, инженеры, и строители используют эти концепции для правильной разметки фундаментов, стен и потолков. Знание о строительных плоскостях позволяет создавать прочные и устойчивые постройки.
Геодезия: Геодезисты используют понятия прямых и параллельных плоскостей для измерения расстояний на земной поверхности и выстраивания точных геометрических моделей местности. Это знание важно при строительстве дорог, тоннелей, а также при проведении гидрографических изысканий.
Автомобильная промышленность: Инженеры, работающие в автомобильной промышленности, учитывают параллельные и пересекающиеся прямые при разработке конструкции подвески автомобилей. Это позволяет создавать автомобили с лучшей устойчивостью и управляемостью на дороге.
Дизайн интерьера: Дизайнеры, создающие интерьеры, часто используют знание о прямых и параллельных линиях для создания гармоничного и сбалансированного пространства. Правильное расположение мебели, рисунка на стенах и размещения светильников основывается на этих концепциях.
Графика и искусство: Художники и дизайнеры используют знание о прямых и параллельных линиях, чтобы создавать перспективу и глубину на своих работах. Они могут использовать эти концепции для создания эффекта глубинного пространства или для создания гармоничных композиций.
Картография: Параллельные и меридиональные линии используются на картах для указания широты и долготы. Изучение этих линий позволяет понять географическое расположение различных местностей и проводить навигацию.
Знание о прямых и параллельных плоскостях имеет широкий спектр применения в различных областях реальной жизни. Оно помогает строить надежные конструкции, создавать гармоничные интерьеры, разрабатывать инновационные автомобили и использовать геометрию для навигации и картографии. Понимание этих концепций позволяет нам лучше взаимодействовать с окружающим миром и расширяет наши возможности в разных областях деятельности.
Советы по правильному использованию лемм о прямых и параллельных плоскостях
Леммы о прямых и параллельных плоскостях используются в различных математических и геометрических задачах. Они позволяют устанавливать связи между прямыми и плоскостями, определять их взаимное расположение и исследовать их свойства.
Ниже приведены несколько советов, которые помогут правильно использовать леммы о прямых и параллельных плоскостях:
| 1. | Внимательно читайте и анализируйте условие задачи. Определите, какие прямые и плоскости заданы и что именно требуется найти. |
| 2. | Используйте леммы о перпендикулярных прямых и о параллельных плоскостях, чтобы установить необходимые связи между геометрическими объектами и получить дополнительные сведения. |
| 3. | Используйте свойства параллельных плоскостей, такие как равенство углов, параллельность соответствующих сторон, равенство площадей фигур и другие, чтобы решать задачи на нахождение неизвестных величин. |
| 4. | Применяйте леммы о прямых и плоскостях только в тех случаях, когда они действительно применимы и дают нужную информацию. Убедитесь, что вы правильно интерпретируете условия задачи и корректно применяете леммы. |
| 5. | При решении задач используйте дополнительные вспомогательные построения и доказательства, чтобы убедиться в правильности полученных результатов. |
| 6. | Не забывайте о проверке полученного ответа. Проверьте его на соответствие условиям задачи и правильность выполнения всех преобразований. |
Соблюдая эти советы, вы сможете правильно использовать леммы о прямых и параллельных плоскостях и успешно решать задачи, связанные с этой темой.



