Математика - это один из фундаментальных предметов, которые обучаются во втором классе. В этом возрасте дети начинают познавать различные геометрические фигуры, включая многоугольники. Многоугольник - это фигура, состоящая из трех или более сторон.
Одним из первых многоугольников, с которым дети сталкиваются, является треугольник. Треугольники - это многоугольники, имеющие три стороны и три угла. Во втором классе дети могут изучать различные типы треугольников, такие как прямоугольный треугольник, равнобедренный треугольник и равносторонний треугольник.
Кроме треугольников, дети также могут учиться распознавать и строить другие многоугольники, такие как четырехугольники (квадраты и прямоугольники) и пятиугольники. Знание этих фигур позволяет детям развивать логическое мышление, а также стимулирует их воображение и творческие способности.
Изучение многоугольников во втором классе математики помогает детям понимать формы и пространственные отношения между объектами. Это важные навыки, которые понадобятся им в дальнейшем, когда они будут изучать более сложные геометрические концепции в старших классах. Поэтому, второй класс является важным этапом в развитии математических навыков и понимания геометрии для молодых учеников.
Классификация многоугольников в математике
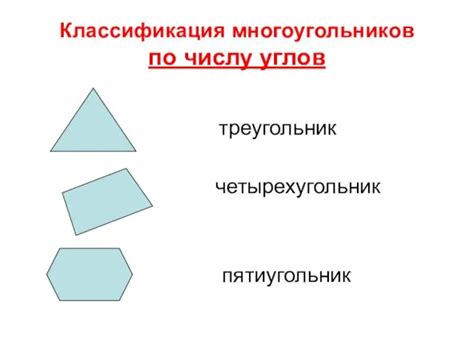
Многоугольники можно классифицировать по количеству сторон. Например:
1. Треугольник - многоугольник, состоящий из трех сторон и трех углов.
2. Четырехугольник - многоугольник, состоящий из четырех сторон и четырех углов. Примерами четырехугольников являются прямоугольник, квадрат и параллелограмм.
3. Пятиугольник - многоугольник, состоящий из пяти сторон и пяти углов. Примером пятиугольника является пентагон.
4. Шестиугольник - многоугольник, состоящий из шести сторон и шести углов. Примером шестиугольника является шестиугольник.
Также многоугольники можно классифицировать по своим свойствам:
1. Равносторонний многоугольник - многоугольник, у которого все стороны имеют одинаковую длину.
2. Равнобедренный многоугольник - многоугольник, у которого углы при основании и противоположные стороны равны.
3. Вписанный многоугольник - многоугольник, все вершины которого лежат на одной окружности.
4. Правильный многоугольник - многоугольник, который является и равносторонним, и равноугольным.
Классификация многоугольников позволяет лучше понять их свойства и использовать эти знания для решения различных геометрических задач и построений. Многоугольники имеют важное значение в математике и могут быть найдены во многих аспектах ежедневной жизни.
Определение и примеры многоугольников
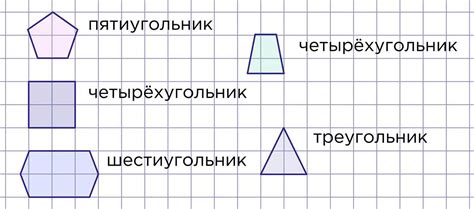
Многоугольники могут быть различных форм и размеров. Наиболее известными и распространенными многоугольниками являются треугольники, четырехугольники (квадраты, прямоугольники, параллелограммы), пятиугольники (пентагоны), шестиугольники (гексагоны) и многоугольники с большим числом сторон.
Примеры многоугольников:
- Треугольник: имеет три стороны.
- Прямоугольник: имеет четыре стороны и углы, прилежащие к двум сторонам, равные 90 градусов.
- Параллелограмм: имеет четыре стороны, противоположные стороны параллельны, и углы, прилежащие к двум сторонам, равные.
- Пентагон: имеет пять сторон.
- Гексагон: имеет шесть сторон.
Многоугольники встречаются повсеместно в природе, архитектуре и других областях, и их изучение широко распространено в математике.
Виды многоугольников
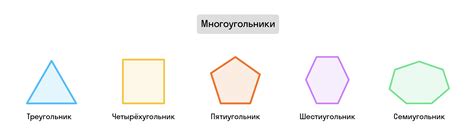
Многоугольник: это фигура, у которой есть закрытая линия, состоящая из отрезков. Количество отрезков в многоугольнике называется числом сторон.
Треугольник: это многоугольник с тремя сторонами.
Четырехугольник: это многоугольник с четырьмя сторонами. Известные примеры таких многоугольников - квадрат, прямоугольник и ромб.
Пятиугольник: это многоугольник с пятью сторонами. Примером пятиугольника может служить звезда с пятью вершинами.
Шестиугольник: это многоугольник с шестью сторонами. Пчелиный сот и снежинка - примеры шестиугольников.
Многоугольники с большим количеством сторон: семиугольник, восьмиугольник, девятиугольник и так далее. Такие многоугольники могут иметь различную форму и называются по числу сторон.
Простой многоугольник: это многоугольник, у которого все углы и стороны равны.
Сложный многоугольник: это многоугольник, у которого есть прямые углы и/или различные длины сторон.
Знание различных видов многоугольников помогает детям лучше понимать и классифицировать геометрические фигуры и развивает их математическое мышление.
Способы измерения и вычисления характеристик многоугольников
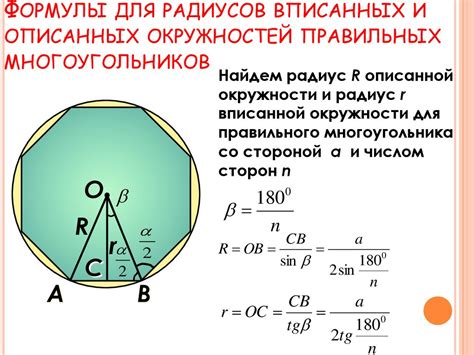
Одной из основных характеристик многоугольника является его периметр - сумма длин всех сторон. Для измерения периметра многоугольника нужно просуммировать длины всех его сторон. Например, для треугольника нужно сложить длины трех сторон, а для четырехугольника - длины четырех сторон.
Другой характеристикой многоугольника является его площадь. Площадь многоугольника показывает, сколько плоской фигуры можно поместить внутри него без наложений и пересечений. Есть несколько способов вычисления площади многоугольника. Один из них - разделение многоугольника на прямоугольники и треугольники, затем нахождение площади каждой фигуры и сложение их.
Если многоугольник правильный, то есть все его стороны и углы равны, можно вычислить его площадь по специальной формуле. Например, для правильного треугольника площадь можно вычислить по формуле S = a^2 * (√3 / 4), где a - длина стороны треугольника.
Также для многоугольника можно вычислить его диагонали - отрезки, соединяющие вершины многоугольника, не являющиеся его сторонами. Диагонали многоугольника могут иметь разные длины и углы.
Для измерения углов многоугольника нужно использовать градусную меру. Угол - это область плоскости, ограниченная двумя сторонами многоугольника. Углы многоугольника могут быть прямыми (90 градусов), острыми (меньше 90 градусов) или тупыми (больше 90 градусов).
| Характеристика | Измерение | Вычисление |
|---|---|---|
| Периметр | Сумма длин сторон | Сложение длин всех сторон многоугольника |
| Площадь | Квадратные единицы площади | Разделение многоугольника на фигуры и сложение их площадей или использование формулы для правильных многоугольников |
| Диагонали | Длина | Измерение отрезков, соединяющих вершины многоугольника |
| Углы | Градусы | Использование градусной меры для измерения углов многоугольника |
Применение многоугольников в реальной жизни

Одно из наиболее распространенных применений многоугольников - это строительство и архитектура. Благодаря своей форме, многоугольники используются для создания основных конструкций зданий. Например, треугольники являются основным строительным блоком для каркаса крыши, а квадраты используются в создании окон и дверей.
В географии также активно используются многоугольники для измерения и описания территорий. Так, границы стран и регионов могут быть заданы в виде многоугольников, что упрощает их обозначение и анализ. Кроме того, многоугольники применяются для построения карт и планов, позволяя наглядно представлять различные объекты и ландшафты.
Также, многоугольники находят применение в графике и дизайне. Они используются для создания форм и фигур, которые используются в различных логотипах, упаковках, мебели и других предметах. Многоугольники помогают придать объектам уникальность, эстетичность и оригинальность.
Кроме того, многоугольники играют важную роль в компьютерной графике и программировании. Они используются для определения форм объектов и их отображения на экране. Геометрические алгоритмы на основе многоугольников позволяют создавать трехмерные модели и создавать реалистичные визуальные эффекты в фильмах, компьютерных играх и анимации.
Таким образом, многоугольники являются неотъемлемой частью нашей жизни и применяются практически во всех областях, связанных с геометрией, строительством и дизайном. Изучение многоугольников помогает улучшить наши навыки анализа форм, вычислений площадей и периметров, а также развивает пространственное мышление и творческие способности.



