Первый принцип, который лежит в основе нашего доказательства, - это закон сохранения массы. Согласно этому закону, масса газа в замкнутой системе остается постоянной при всех изменениях его состояния. Это значит, что если мы возьмем определенное количество газа и изменим его давление, объем или температуру, то масса газа останется неизменной.
Второй принцип, на котором базируется наше доказательство, - это закон Бойля-Мариотта. Он устанавливает обратную зависимость между давлением и объемом газа при постоянной температуре: при увеличении давления объем газа уменьшается, а при уменьшении давления - увеличивается. Этот закон может быть проверен путем эксперимента с помощью устройства, называемого манометром.
Третий принцип, который мы используем в нашем доказательстве, - это закон Шарля. Он гласит, что объем газа при постоянном давлении изменяется пропорционально его температуре: при увеличении температуры объем газа увеличивается, а при уменьшении температуры - уменьшается. Этот закон может быть проверен с помощью специального устройства, называемого мерной колбой.
Принцип доказательства уравнения состояния газа

В основе доказательства лежит модель идеального газа, которая удовлетворяет уравнению состояния PV = nRT, где P - давление газа, V - объем газа, n - количество вещества газа, R - универсальная газовая постоянная, T - абсолютная температура газа.
Для доказательства уравнения состояния газа можно использовать различные методы и опыты. Одним из наиболее простых и надежных методов является опыт с газом в ограниченном объеме. В этом опыте газ заключается в сосуде с подвижным поршнем или воздушном шаре.
В ходе опыта газ подвергается изменению давления, объема и температуры. При этом измеряются соответствующие значения величин и устанавливаются связи между ними. Например, при постоянной температуре и изменении объема, давление газа будет изменяться пропорционально. Эти наблюдения подтверждают уравнение состояния газа.
Таким образом, принцип доказательства уравнения состояния газа основан на изучении зависимости между давлением, объемом и температурой газа. Этот принцип играет важную роль в изучении газов и является основой для решения различных задач и проблем, связанных с газовой динамикой и термодинамикой.
Формула и ее надежность
| Уравнение состояния газа: | PV = nRT |
|---|
где:
- P - давление газа
- V - объем газа
- n - количество вещества газа
- R - универсальная газовая постоянная
- T - температура газа в кельвинах
Это уравнение позволяет рассчитать состояние газа при заданных параметрах или определить один из параметров, если известны остальные. Например, можно рассчитать давление газа при заданном объеме, количестве вещества и температуре.
Надежность уравнения состояния газа подтверждается его использованием для описания поведения газов в различных системах. Величина универсальной газовой постоянной R является константой и имеет одни и те же значения для всех газов. Это позволяет применять уравнение состояния газа также для сравнения разных газов между собой.
Однако, следует учитывать, что уравнение состояния газа считается верным только при определенных условиях, таких как низкое давление и высокая температура, или когда газы находятся в идеальном состоянии. В реальности, существуют некоторые отклонения от идеального поведения газов, которые не учитываются этим уравнением. Для более точного описания поведения газов, можно использовать модифицированные уравнения состояния, такие как уравнение Ван-дер-Ваальса и другие.
Учет влияния температуры и давления
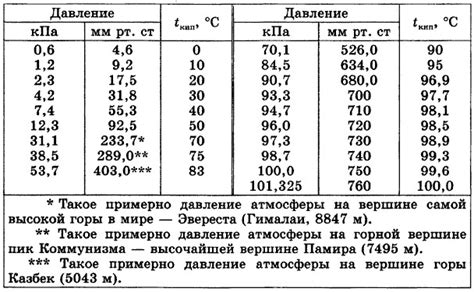
Уравнение состояния газа учитывает влияние температуры и давления на поведение газовой смеси. При изменении температуры или давления газ изменяет свои свойства, включая объем, давление и температуру.
Учет влияния температуры осуществляется путем введения температуры в уравнение состояния газа. Температура измеряется в градусах Цельсия (°C) или Кельвинах (K) и указывает на среднюю кинетическую энергию молекул газа. По мере увеличения температуры, молекулы газа приобретают большую кинетическую энергию и начинают двигаться быстрее, что приводит к увеличению объема газа.
Учет влияния давления осуществляется путем введения давления в уравнение состояния газа. Давление измеряется в паскалях (Па), барах (bar) или атмосферах (атм). Высокое давление означает, что на газ действует большая сила, что приводит к уменьшению его объема. Низкое давление, наоборот, позволяет газу расширяться и занимать больший объем.
- При повышении температуры и постоянном давлении объем газа увеличивается.
- При повышении давления и постоянной температуре объем газа уменьшается.
- При повышении температуры и повышении давления влияние на объем газа будет определяться компромиссом между двумя факторами.
Учет влияния температуры и давления в уравнении состояния газа позволяет более точно описывать поведение газовой смеси и проводить различные расчеты, например, рассчитывать изменение объема газа при изменении температуры или давления.
Основные предположения уравнения состояния газа

Однако, прежде чем перейти к рассмотрению самого уравнения, необходимо ознакомиться с некоторыми основными предположениями, на которых оно основано. Вот основные предположения уравнения состояния газа:
- Идеальность газа: В уравнении состояния газа предполагается, что газ является идеальным, то есть не имеет силы притяжения или отталкивания молекул. Это предположение обосновано в случае разреженных газов и высоких температур, когда межмолекулярные взаимодействия становятся незначительными.
- Молекулярная структура: Уравнение состояния газа основано на представлении о газе как состоящем из молекул, которые движутся хаотически. Однако, для упрощения расчетов, предполагается, что движение молекул нерегулярно и предсказать точные траектории молекул невозможно.
- Постоянство количества вещества: Уравнение состояния газа предполагает, что количество вещества газа остается неизменным. Это означает, что в процессе изменения давления, объема и температуры газа, количество молекул газа остается постоянным.
- Закон сохранения энергии: Уравнение состояния газа основано на законе сохранения энергии, который утверждает, что энергия не создается и не уничтожается, а только переходит из одной формы в другую. Это предположение позволяет рассчитывать изменение энергии газа при изменении его состояния.
Используя эти основные предположения, уравнение состояния газа позволяет математически описать зависимость между давлением, объемом и температурой газа и использовать его в различных сферах науки и техники.
Примеры практического применения уравнения состояния газа

1. Расчет давления и объема газа в реакционных сосудах: Уравнение состояния газа позволяет определить давление и объем газа в реакционных сосудах при различных условиях температуры и давления. Это важно для контроля и оптимизации химических реакций, происходящих в таких сосудах.
2. Расчет объема сжатого газа: Уравнение состояния газа также используется для определения объема газа после его сжатия при известной температуре и давлении. Это помогает в инженерии и строительстве, где необходимо знать конечный объем газа после его сжатия.
3. Оценка физических свойств газов: Уравнение состояния газа полезно для оценки различных физических свойств газов, таких как плотность, молярная масса, теплоемкость и вязкость. Это позволяет проводить расчеты и моделирование различных процессов и явлений, связанных с газами.
4. Расчет состава газовой смеси: Уравнение состояния газа позволяет определять состав газовых смесей, основываясь на их температуре, давлении и объеме. Это важно в промышленности, где необходимо контролировать и оптимизировать состав газовых смесей для различных процессов.
5. Прогнозирование поведения газов: Уравнение состояния газа используется для прогнозирования поведения газов, например, при изменении температуры или давления. Это позволяет предсказывать, как газ будет себя вести в различных условиях и планировать соответствующие меры безопасности.
В конечном счете, уравнение состояния газа имеет широкий спектр применения и является основным инструментом для анализа и понимания поведения газов в различных условиях.
Ограничения и проблемы уравнения состояния газа

Одним из главных ограничений уравнения состояния газа является его применимость только к идеальным газам. Идеальный газ представляет собой гипотетическую модель, в которой атомы или молекулы газа не взаимодействуют друг с другом и не занимают объем. В реальности же такое поведение газа наблюдается только при высоких температурах и низких давлениях.
Другой проблемой уравнения состояния газа является его неприменимость к ситуациям, когда газ находится в критическом состоянии или близко к нему. В критической точке свойства газа изменяются настолько сильно, что уравнение состояния становится неприменимым.
Кроме того, уравнение состояния газа не учитывает влияние межмолекулярных сил на поведение газа. В реальности молекулы газа взаимодействуют друг с другом, что может приводить к изменению их объема и давления. Для учета этих эффектов необходимо использовать более сложные модели.
Также следует отметить, что уравнение состояния газа основано на предположении, что газ является одноатомным или двухатомным. Для более сложных молекул необходимо использовать модифицированные версии уравнения.
| Ограничение/проблема | Важность |
|---|---|
| Применимость только к идеальным газам | Средняя |
| Неприменимость к критическому состоянию газа | Высокая |
| Незаметность межмолекулярных взаимодействий | Высокая |
| Ограниченность для сложных молекул | Средняя |
Не смотря на эти ограничения, уравнение состояния газа все же остается полезным инструментом для описания поведения и предсказания свойств газовых смесей во многих практических приложениях.



