В геометрии параллелограмм - это четырехугольник, у которого противоположные стороны параллельны. Существует несколько методов доказательства того, что данный четырехугольник является параллелограммом.
Один из самых простых методов - это доказательство с использованием свойств параллельных прямых. Если две противоположные стороны параллельны, то их углы при пересечении с третьей стороной будут смежными и равными, а также сумма противоположных углов будет равна 180 градусам. Это свойство можно использовать для доказательства параллелограмма.
Еще один метод - это доказательство с использованием свойств диагоналей. Для параллелограмма характерно то, что диагонали пересекаются на серединах и делятся пополам. Таким образом, можно показать, что диагонали параллелограмма имеют равную длину, и их точка пересечения делит каждую диагональ пополам.
Также можно использовать метод доказательства с использованием векторов. Если для векторов, соответствующих сторонам параллелограмма, выполнено условие равенства модуля, направления и суммы данных векторов, то это является доказательством параллелограмма.
В данной статье будут рассмотрены подробности этих и других методов доказательства параллелограмма в геометрии.
Параллелограмм: определение и основные свойства
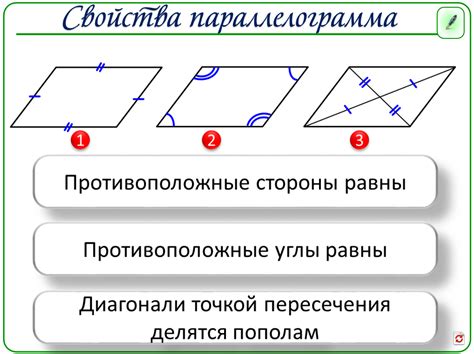
Основные свойства параллелограмма:
- Противоположные стороны параллельны: параллелограмм имеет две противоположные стороны, которые являются параллельными прямыми.
- Противоположные стороны равны: длины противоположных сторон параллелограмма равны между собой.
- Противоположные углы равны: углы, образованные параллельными сторонами и другими сторонами параллелограмма, равны между собой.
- Соседние углы дополнительны: соседние углы параллелограмма дополняют друг друга до 180 градусов.
- Диагонали делятся пополам: диагонали параллелограмма делятся пополам и пересекаются в точке, которая является серединой каждой диагонали.
Параллелограммы широко используются в геометрии и имеют множество применений. Они являются основой для изучения многих других фигур и моделей, а также используются в различных областях, включая инженерию, архитектуру и физику.
Свойства и конструкция параллелограмма
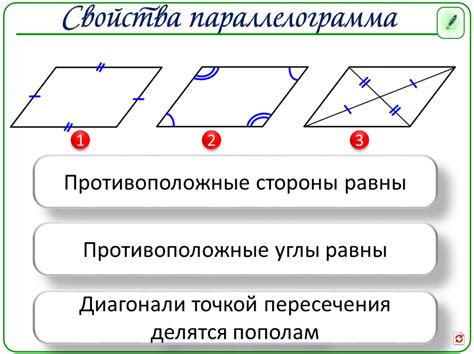
У параллелограмма есть несколько свойств:
- Противоположные стороны параллельны и равны: AB‖CD и AB = CD, BC‖AD и BC = AD.
- Противоположные углы параллелограмма равны: ∠A = ∠C, ∠B = ∠D.
- Сумма углов параллелограмма равна 360°: ∠A + ∠B + ∠C + ∠D = 360°.
- Диагонали параллелограмма делятся пополам и пересекаются в точке О, которая является серединой каждой диагонали.
- Стороны параллелограмма образуют две пары равных и подобных треугольников.
Параллелограмм можно построить с помощью различных способов:
- Способ 1: Начертите отрезок AB (сторону параллелограмма) заданной длины. На одном из концов А постройте угол, равный одному из углов параллелограмма (используя циркуль и неразмеченную линейку). Проведите из второго конца В угла линию BC (другую сторону параллелограмма) такую, чтобы она пересекла отрезок АС. Проведите из точки А параллельную линию к BC (прямую отрезка BC), а из точки С – параллельную AB. Полученный четырехугольник ABCD является параллелограммом.
- Способ 2: Начертите отрезок AC (диагональ параллелограмма) заданной длины. На одном из концов А постройте угол, равный одному из углов параллелограмма (используя циркуль и неразмеченную линейку). Опишите окружность радиусом, равным диагонали АС. Проколите центр окружности. Постройте вторую диагональ BD, проведя её из точки А до пересечения с окружностью. Полученный четырехугольник ABCD является параллелограммом.
- Способ 3: Начертите отрезок AB (сторона параллелограмма) заданной длины. На одном из концов А постройте угол, равный одному из углов параллелограмма (используя циркуль и неразмеченную линейку). Окружность радиусом, равным диагонали АС, опишите так, чтобы ее центр совпадал с противоположной точкой B. Проколите центр окружности. Из центра окружности проведите вторую диагональ CD. Полученный четырехугольник ABCD является параллелограммом.
Зная свойства и методы построения параллелограмма, можно успешно применять их в геометрических задачах и доказательствах.
Методы доказательства параллелограмма через равенство сторон и углов

1. Метод равных сторон. Он основан на том, что если в параллелограмме две стороны равны, то противоположные стороны также равны. Если стороны AB и BC параллелограмма равны, то и стороны AD и CD равны. Аналогично, если стороны BC и AD равны, то и стороны AB и CD равны.
2. Метод равных углов. В этом методе используется факт, что если в параллелограмме два угла равны, то противоположные углы также равны. Если угол A равен углу C, то и угол B также равен углу D. Аналогично, если угол B равен углу D, то и угол A равен углу C.
3. Метод равных сторон и углов. В этом методе используются как равные стороны, так и равные углы параллелограмма. Если в параллелограмме две стороны равны и прилежащие им углы равны, то все стороны и углы параллелограмма равны.
Таким образом, существует несколько методов доказательства параллелограмма, которые позволяют установить его свойства через равенство сторон и углов: метод равных сторон, метод равных углов и метод равных сторон и углов.
Методы доказательства параллелограмма через середины сторон

Если у нас имеется четырехугольник ABCD, то чтобы доказать, что он является параллелограммом, необходимо убедиться в выполнении двух условий:
- Середина отрезка AB совпадает с серединой отрезка CD;
- Середина отрезка BC совпадает с серединой отрезка AD.
Чтобы это доказать, можно использовать таблицу для представления данных:
| Условие | Доказательство |
|---|---|
| Середина AB = середина CD | Для доказательства этого условия можно использовать следующие шаги: |
| 1. Обозначим точку M как середину отрезка AB. | |
| 2. Обозначим точку N как середину отрезка CD. | |
| 3. Используя свойство серединного перпендикуляра, докажем, что отрезок MN перпендикулярен отрезку AB. | |
| 4. Используя свойство серединного перпендикуляра, докажем, что отрезок MN перпендикулярен отрезку CD. | |
| 5. Из полученных результатов следует, что отрезок AB параллелен отрезку CD. | |
| Середина BC = середина AD | Доказательство этого условия аналогично доказательству первого условия, только с заменой отрезков AB и CD на отрезки BC и AD соответственно. |
Таким образом, доказательство параллелограмма ABCD с использованием метода через середины сторон заключается в доказательстве равенства серединных точек сторон четырехугольника. Если оба указанных условия выполняются, мы можем утверждать, что ABCD является параллелограммом.
Методы доказательства параллелограмма с использованием векторов
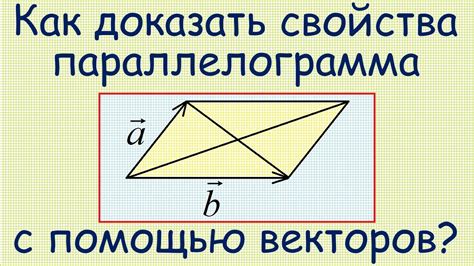
Для доказательства параллельности сторон параллелограмма с использованием векторов можно воспользоваться следующими шагами:
Вычислить векторы каждой из сторон параллелограмма при помощи формулы вектора: AB = B - A, где А и В – координаты концов стороны.
Установить, являются ли векторы, соответствующие противоположным сторонам параллелограмма, равными по модулю и противоположными по направлению. Если это так, то стороны параллелограмма параллельны.
Проверить, являются ли диагонали параллелограмма равными и попарно средними линиями. Для этого можно вычислить векторы диагоналей и проверить их равенство. Если векторы равны, то диагонали параллелограмма равны и попарно средние линии.
Векторный метод доказательства параллелограмма позволяет проверить параллельность сторон и равенство диагоналей с помощью анализа векторов. Он экономит время и усилия, особенно при работе с большими числами или сложными четырехугольниками. Однако, для его использования требуется хорошее знание векторной алгебры и умение применять соответствующие формулы.



