Среднее арифметическое является наиболее распространенной мерой центральной тенденции. Оно рассчитывается путем сложения всех значений в совокупности данных и деления полученной суммы на количество значений. Среднее арифметическое позволяет получить общую картину о данных, хотя оно может быть смещено выбросами.
Медиана является другой мерой центральной тенденции. Она представляет собой значение, которое располагается посередине в упорядоченных данных. Если число значений нечетное, медиана представляет собой значение, которое точно находится в середине. Если число значений четное, медиана представляет собой среднее арифметическое двух средних значений.
В этом полном руководстве мы рассмотрим различные меры центральной тенденции, их особенности и методы расчета. Мы покажем важность правильного выбора меры центральной тенденции в зависимости от типа данных и целей исследования. Вы узнаете, как интерпретировать и использовать полученные результаты для принятия обоснованных решений. Приступим к изучению мер центральной тенденции и повышению Ваших навыков в статистике!
Зачем нужны меры центральной тенденции данных?

Основная задача мер центральной тенденции данных - описать распределение данных, определить наиболее типичные значения и предоставить общую "картину" данной совокупности. Эти меры могут быть использованы для принятия решений, проведения сравнений и выявления отклонений в данных.
Одной из наиболее распространенных мер центральной тенденции является среднее арифметическое или среднее значение. Оно показывает среднюю величину всех данных в выборке и используется во многих областях, таких как экономика, наука, физика и социология. Другой распространенной мерой является медиана, которая является центральным значением данных и разделяет выборку на две равные части. Мода, третья мера центральной тенденции, показывает наиболее часто встречающееся значение в выборке.
Меры центральной тенденции данных также могут помочь в выявлении аномалий, выбросов или ошибок в данных. Если какое-то значение является значительно отличающимся от других значений в выборке, это может указывать на наличие ошибки или важную информацию, которую следует рассмотреть отдельно.
Различные виды мер центральной тенденции

Меры центральной тенденции используются в статистике для определения среднего значения или типичного значения набора данных. Они позволяют суммировать и анализировать информацию о совокупности данных, учитывая все ее значения.
Существует несколько видов мер центральной тенденции, каждый из которых имеет свое значение и применение:
Среднее арифметическое (среднее) - это наиболее распространенная и простая мера центральной тенденции. Оно вычисляется путем суммирования всех значений и деления полученной суммы на количество значений. Среднее арифметическое представляет "среднюю" величину в наборе данных.
Медиана - это значение, которое занимает центральное место в упорядоченном списке значений. Для вычисления медианы набор данных сортируется по возрастанию или убыванию, и затем находится значение, которое находится посередине списка. Медиана является робастной мерой центральной тенденции, что означает, что она менее чувствительна к выбросам или экстремальным значениям.
Мода - это значение, которое встречается чаще всего в наборе данных. Если есть несколько значений, которые встречаются с одинаковой частотой и чаще других, то такие значения называются "модальными". Мода позволяет исследовать наиболее типичное или часто встречающееся значение в наборе данных.
Каждая из этих мер центральной тенденции имеет свои преимущества и предпочтения в конкретных ситуациях. Выбор меры зависит от целей и особенностей анализа данных.
Как выбрать подходящую меру центральной тенденции?

Существует несколько различных мер центральной тенденции, и выбор подходящей зависит от различных факторов и характеристик данных. Вот несколько важных вопросов, о которых нужно задуматься при выборе меры центральной тенденции:
- Тип данных: Нужно определить тип данных, с которым вы работаете. Если у вас непрерывные данные, то среднее арифметическое значение (среднее) может быть хорошим выбором. Если ваши данные являются категориальными или номинальными, то мода (наиболее частое значение) может быть предпочтительной мерой центральной тенденции.
- Распределение данных: Изучение формы распределения данных также поможет определить подходящую меру центральной тенденции. Для симметрично распределенных данных среднее значение (среднее) может быть хорошим выбором. Если данные имеют асимметричное распределение, то медиана (середина набора данных, разделяющая половины) может более точно представлять центральную тенденцию.
- Чувствительность к выбросам: Если в ваших данных есть выбросы (выдающиеся значения), то выбор меры центральной тенденции также может зависеть от чувствительности к выбросам. Среднее значение может быть чувствительно к выбросам, так как оно учитывает все значения в совокупности данных. Медиана, с другой стороны, более устойчива к выбросам, так как она основана только на серединном значении.
Итак, при выборе подходящей меры центральной тенденции необходимо учитывать тип данных, форму распределения данных и чувствительность к выбросам. Кроме того, иногда может быть полезно рассмотреть несколько мер центральной тенденции, чтобы получить полноту картину о данных.
Применение мер центральной тенденции в практике
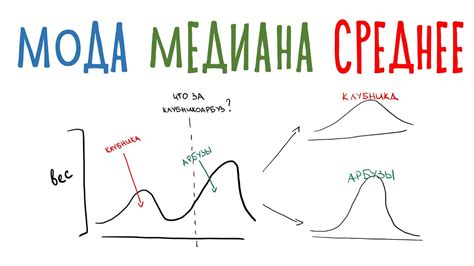
Одной из основных мер центральной тенденции является среднее арифметическое значение, или средняя. Она вычисляется путем суммирования всех значений и деления на количество наблюдений. Среднее позволяет получить представление о типичном значении в совокупности данных.
Еще одной важной мерой центральной тенденции является медиана. Медиана представляет собой значение, разделяющее совокупность данных на две равные части - 50% значений находятся выше медианы, и 50% значений - ниже. Медиана позволяет оценить "середину" данных и не зависит от выбросов в данных.
Модуль - это еще одна мера центральной тенденции, представляющая значение, которое встречается наиболее часто. Мода может быть полезна, когда необходимо определить наиболее популярное значение в данных.
В зависимости от типа данных и цели анализа, различные меры центральной тенденции могут быть применены. Например, среднее и медиана часто используются в экономической и социологической статистике для оценки доходов или распределения доходов в совокупности населения. В медицинских исследованиях может быть полезна мода для определения наиболее частых симптомов или диагнозов.



