Математика - это одна из самых фундаментальных и универсальных наук, которая изучает свойства и взаимоотношения чисел, фигур и абстрактных объектов. Во многих учебниках и программных средах программирования существует правило, что операции умножения и деления выполняются одновременно и выполняются слева направо. Однако, существует множество споров и несогласий касательно того, какая операция выполняется первой: деление или умножение?
Когда в математическом выражении встречаются операции умножения и деления, важно понимать, что сначала выполняется операция, которая встречается первой слева. Например, в выражении "6 ÷ 2 × 3" сначала выполняется деление 6 на 2, а затем умножение полученного результата на 3. Таким образом, результат выражения будет равен 9.
На самом деле, операции умножения и деления имеют одинаковый приоритет и выполняются в том порядке, в котором они встречаются в выражении. То есть, если умножение встречается перед делением, оно будет выполнено первым. Если же деление встречается перед умножением, оно будет выполнено первым. Это правило помогает избежать путаницы и получить правильный результат вычисления.
Математика - деление или умножение
Ответ на этот вопрос дает нам установленная в математике порядок выполнения операций, известный как правило "больше, меньше". Это правило гласит, что умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Таким образом, при выполнении выражения или задачи, содержащей оба этих знака, сначала выполняются деление и умножение, а затем сложение и вычитание.
Если в выражении присутствуют только умножение и деление без других операций, то выполняются они слева направо. Например, в выражении 4 / 2 * 3 будет выполнено деление 4 / 2, что равно 2, а затем умножение 2 * 3, что равно 6.
Однако существуют случаи, когда порядок операций можно изменить с помощью использования скобок. Если в выражении есть скобки, то сначала выполняются операции внутри скобок, а затем уже остальные действия.
Поэтому для того, чтобы точно определить, что выполняется первым - деление или умножение, необходимо помнить о правиле "больше, меньше" и учитывать наличие скобок в выражении. Таким образом, математика предлагает нам четкий порядок действий, который позволяет получить верный результат вычислений.
Первоначальные понятия в математике

Одним из первоначальных понятий в математике является операция сложения. Сложение позволяет объединить два или более числа в одно и представляет собой основной способ комбинирования и увеличения величин. При совершении операции сложения, результат называется суммой или их суммой. Для изображения сложения в математике используют знак "+".
Другой важной операцией в математике является операция вычитания. Вычитание используется для нахождения разности между двумя числами. При совершении операции вычитания, результат называется разностью. Для изображения операции вычитания в математике используется знак "-".
Умножение - это операция, которая позволяет умножить два числа, называемые множителями, для получения их произведения. Результат операции умножения называется произведением. Умножение может быть представлено с помощью знака "*".
Деление - это операция, которая позволяет разделить одно число на другое. Результат операции деления называется частным. Для изображения операции деления в математике используется знак "/".
Порядок выполнения операций в математике определяется приоритетом операций. Обычно умножение и деление выполняются раньше сложения и вычитания. Однако, при необходимости можно использовать скобки для изменения порядка выполнения операций.
| Операция | Знак | Пример | Результат |
|---|---|---|---|
| Сложение | + | 5 + 3 | 8 |
| Вычитание | - | 7 - 4 | 3 |
| Умножение | * | 2 * 6 | 12 |
| Деление | / | 10 / 2 | 5 |
Понимание этих первоначальных понятий в математике является фундаментальным для дальнейшего изучения и применения математических концепций в решении различных задач.
Определение деления и умножения
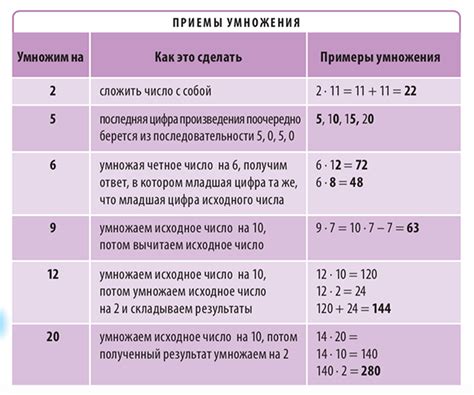
Деление - это процесс разделения одного числа на другое равными частями. В делении присутствуют четыре основных компонента: делимое, делитель, частное и остаток. Делимое - это число, которое нужно разделить, делитель - число, на которое делится делимое, частное - результат деления, а остаток - число, которое остается после деления делимого на делитель.
Умножение - это процесс, при котором одно число увеличивается в разы, указанные другим числом. Умножение также состоит из трех основных компонентов: множитель, умножаемое и произведение. Множитель - это число, на которое умножается умножаемое, умножаемое - число, которое увеличивается, а произведение - результат умножения.
Порядок выполнения операций в математике определен для обеспечения однозначности результатов. По соглашению, в выражениях смешанных операций деление обычно выполняется первым, а затем следует умножение.
Приоритет операций в математике

Математика включает в себя различные операции, такие как сложение, вычитание, умножение и деление. Однако, при выполнении математических выражений, существует правила приоритета операций, которые определяют порядок выполения операций.
Согласно правилам приоритета операций:
- Выполняются операции в скобках;
- Затем выполняются операции умножения и деления, в порядке их появления;
- Наконец, выполняются операции сложения и вычитания, также в порядке их появления.
Это означает, что операции в скобках имеют самый высокий приоритет и выполняются первыми. Затем умножение и деление выполняются перед сложением и вычитанием.
Например, если у нас есть выражение: 3 + 4 * 2, сначала умножение выполняется первым (4 * 2 = 8), а затем сложение (3 + 8 = 11).
Эти правила приоритета операций помогают обеспечить однозначность и правильное выполнение математических выражений.
Выполнение операций слева направо

При выполнении математических операций, включая деление и умножение, общепринято правило выполнения операций слева направо.
Это означает, что при наличии нескольких операций умножения и деления в одном выражении, они выполняются по порядку, начиная с самого левого оператора.
Например, в выражении 6 ÷ 3 × 2, сначала выполняется деление 6 ÷ 3, что дает результат 2, а затем происходит умножение 2 × 2, результатом которого является 4.
Таким образом, при выполнении операций слева направо мы получаем последовательность шагов, которая определяет конечный результат.
Важно помнить, что при использовании скобок мы можем изменить порядок выполнения операций, приоритетности операторов или группировки чисел.
Правило выполнения операций слева направо является одним из основных принципов математики и позволяет получать точный результат при выполнении сложных выражений.
Примеры выполнения операций
Рассмотрим некоторые примеры выполнения операций деления и умножения:
1) Приоритет операций: расчет выполняется слева направо. Например, в следующем примере:
- 10 / 2 * 5 = 25
Сначала выполняется деление 10 на 2, получаем 5. Затем это значение умножается на 5, и в итоге получаем 25.
2) При использовании скобок можно изменить порядок выполнения операций. Например:
- (10 / 2) * 5 = 25
- 10 / (2 * 5) = 1
В первом примере скобки указывают, что сначала нужно выполнить операцию деления, затем умножения. Во втором примере скобки указывают, что сначала нужно выполнить операцию умножения, затем деления.
3) При использовании одновременно разных операций, приоритет может быть определен по правилу "умножение и деление выполняются до сложения и вычитания". Например:
- 10 + 2 * 5 = 20
- 10 - 2 / 5 = 9.6
В первом примере умножение выполняется раньше сложения, а во втором примере деление выполняется раньше вычитания.
Операции деления и умножения выполняются по правилам математики, которые позволяют добиться однозначности выполнения выражений. Правильное понимание порядка выполнения операций позволяет правильно решать математические задачи и получать корректные результаты.
Влияние скобок на приоритет операций
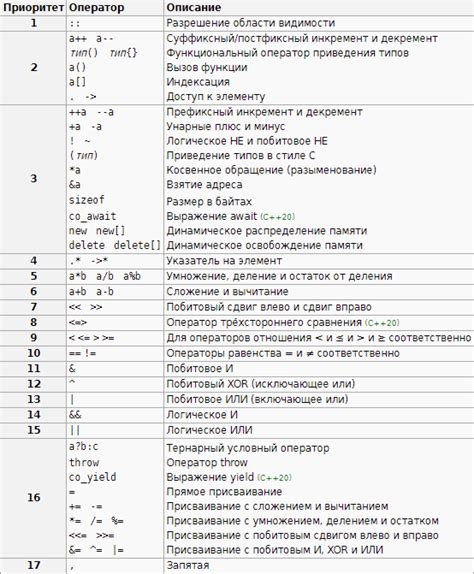
Использование скобок позволяет явно указать, какие операции должны быть выполнены первыми, а какие - последними. Применение скобок позволяет избежать путаницы и неоднозначности при интерпретации математического выражения.
Например, рассмотрим выражение 4 * 2 + 3. Без скобок это выражение может быть интерпретировано двумя способами: либо сначала умножение, затем сложение (4 * 2 + 3 = 11), либо сначала сложение, затем умножение (4 * (2 + 3) = 20). Однако если мы явно укажем порядок операций с помощью скобок, например, (4 * 2) + 3, то станет очевидно, что сначала нужно выполнить умножение, а затем сложение (4 * 2 + 3 = 11).
Итак, скобки позволяют контролировать порядок выполнения операций и обеспечивают ясность и однозначность математических выражений. Правильное использование скобок является важным аспектом успешного решения математических задач и избегания ошибок.
Механизм работы компьютерных программ
Компьютерные программы представляют собой набор инструкций, написанных на языке программирования, которые компьютер может понять и выполнить. Работа программы основана на последовательном выполнении команд компьютером.
Когда программа запускается, она загружается в оперативную память компьютера. Затем происходит ее исполнение, то есть компьютер последовательно выполняет каждую команду в программе.
Важно понимать, что компьютеры работают со множеством различных типов данных, таких как числа, строки, булевы значения и другие. Используя операторы и функции языка программирования, программист может производить операции над этими данными.
При выполнении программы компьютер проходит по ее инструкциям, выполняя арифметические операции, сравнения, условные ветвления, циклы и другие конструкции. Программист может использовать различные алгоритмы и структуры данных для решения конкретных задач.
Очень важно следить за порядком выполнения операций в программе. Например, в математике и программировании есть правила приоритета операций. Например, умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Это значит, что при выполнении программы компьютер сначала выполнит умножение и деление, а затем сложение и вычитание.
Механизм работы компьютерных программ весьма сложен и требует от программиста четкого понимания процесса выполнения программы. Но когда все инструкции программы выполняются последовательно и правильно, можно достичь желаемого результата.



