Криволинейное движение – одно из наиболее сложных явлений в физике, которое изучает движение объектов по траекториям, не являющимся прямыми линиями. В отличие от прямолинейного движения, криволинейное движение происходит по изогнутым или волнистым путям, что требует дополнительных знаний и навыков для его анализа и описания.
Понимание криволинейного движения имеет важное значение в физике, так как многие естественные и технические процессы в реальном мире происходят именно по криволинейным траекториям. Например, это может быть движение частицы в магнитном поле, траектория падения тела под углом или движение автомобиля по извилистой дороге.
Для полного понимания криволинейного движения необходимо знать основные понятия и законы физики, связанные с этим явлением. Важно учесть скорость и ускорение объекта, а также направление и модуль этих величин на каждый момент времени. В зависимости от характера траектории и зависимости этих параметров, криволинейное движение может быть разделено на несколько типов: равномерное и неравномерное, прямолинейное и криволинейное, и т.д.
Изучение криволинейного движения позволяет получить более полное представление о физических явлениях и процессах, происходящих в нашем мире. Благодаря анализу и математическому описанию такого движения физики могут прогнозировать поведение тел и создавать более эффективные и точные модели для объяснения явлений в природе и технике.
Определение и основные понятия

Основными понятиями, связанными с криволинейным движением, являются:
| Траектория | Путь, по которому движется тело. В криволинейном движении траектория может быть закрытой (как, например, в случае движения по окружности) или открытой (как, например, в случае движения по эллипсу). |
| Скорость | Величина, определяющая изменение пути за единицу времени. В криволинейном движении скорость может меняться в зависимости от направления движения. |
| Ускорение | Величина, определяющая изменение скорости за единицу времени. В криволинейном движении ускорение может иметь как направление, так и величину. |
| Радиус кривизны | Величина, определяющая кривизну траектории движения. В криволинейном движении радиус кривизны может меняться, что приводит к изменению характера движения. |
Изучение криволинейного движения позволяет более точно описывать и предсказывать движение тела в различных ситуациях, таких как движение спутников, движение автомобилей по дорогам, движение электронов в атомах и многих других.
Траектория движения в криволинейной системе координат

В криволинейной системе координат траектория движения может быть представлена в виде кривой линии, которая описывает путь движения объекта. Такая кривая линия может иметь различные формы, например, окружность, эллипс, параболу или гиперболу.
Траектория движения в криволинейной системе координат может быть определена с помощью уравнений, которые связывают координаты объекта в различные моменты времени. Такие уравнения могут быть дифференциальными или интегральными и зависят от конкретной задачи и условий движения.
Анализ и изучение траектории движения в криволинейной системе координат позволяет определить различные характеристики движения, такие как скорость, ускорение и т.д. Кроме того, знание траектории позволяет предсказывать путь движения объекта в будущем и прогнозировать его поведение в различных ситуациях.
Векторное представление криволинейного движения
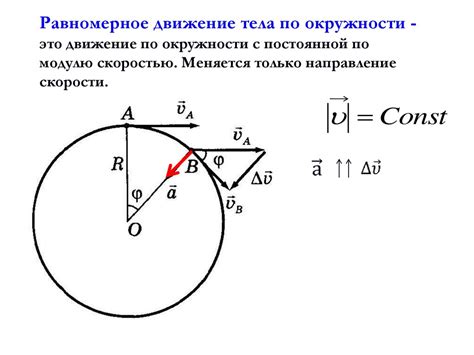
Для описания криволинейного движения необходимо задать два вектора: радиус-вектор, указывающий положение тела относительно начала координат, и вектор скорости, указывающий направление и величину скорости тела.
Радиус-вектор обычно обозначается символом r и задается в виде векторной функции от времени: r(t) = x(t)i + y(t)j + z(t)k, где x(t), y(t) и z(t) - функции времени, определяющие положение тела по координатам x, y и z соответственно, а i, j и k - единичные векторы, указывающие направление осей координат.
Вектор скорости обычно обозначается символом v и задается как производная радиус-вектора по времени: v(t) = dx(t)/dt i + dy(t)/dt j + dz(t)/dt k. Вектор скорости указывает направление и величину скорости тела в каждый момент времени.
Векторное представление криволинейного движения позволяет более точно описать движение тела по сложной кривой траектории. Оно учитывает изменение скорости и направления движения, что является необходимым для анализа многих физических процессов.
Примеры криволинейного движения
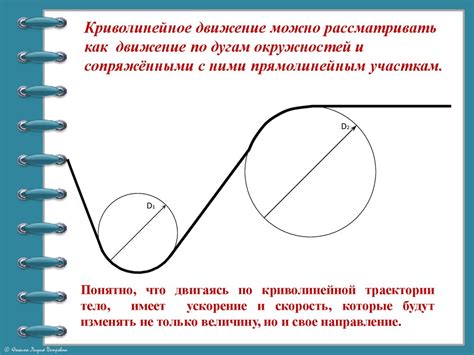
Один из примеров криволинейного движения - это движение планет вокруг своих осей. Например, Земля вращается вокруг своей оси, при этом траектория точки на поверхности Земли будет криволинейной. Кроме того, планеты движутся по эллиптическим орбитам вокруг Солнца, что также является примером криволинейного движения.
Второй пример криволинейного движения - это движение автомобиля по изогнутой дороге. При движении по изгибам и поворотам, автомобиль изменяет свою траекторию и движется по криволинейной траектории. Это происходит из-за того, что силы трения и центробежные силы воздействуют на автомобиль и изменяют его направление движения.
Третий пример криволинейного движения - это движение проектайла. Проектайл - это объект, который брошен в воздух под углом к горизонту. Он движется по параболической траектории, которая является криволинейной. Такое движение проектайла можно наблюдать, например, при броске мяча или пули.
Это лишь несколько примеров криволинейного движения, которые можно встретить в реальной жизни. Криволинейное движение является важным понятием в физике и позволяет описывать различные процессы и явления.
Применение криволинейного движения в физике
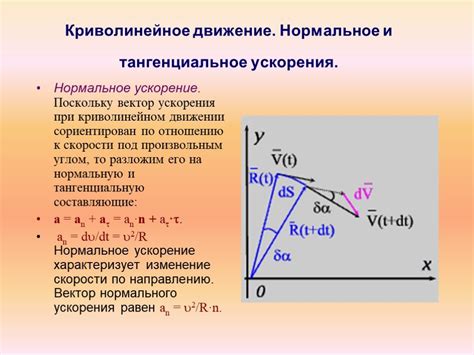
Одно из основных применений криволинейного движения – моделирование движений реальных объектов. Многие движения в природе и в технике происходят по криволинейным траекториям, и изучение их позволяет нам лучше понять поведение физических систем и предсказывать их будущее состояние.
Например, при изучении движения планет вокруг Солнца физики применяют модели криволинейного движения, чтобы объяснить наблюдаемые изменения скорости и направления движения планет. Также, криволинейное движение используется при изучении движения электронов в атомах и молекулах, что позволяет предсказывать и объяснять их химические свойства.
В технике криволинейное движение находит широкое применение при проектировании и управлении сложными системами. Например, при разработке роботов и автоматизированных систем используется криволинейное движение для оптимального перемещения и манипулирования объектами.
Кроме того, понимание принципов криволинейного движения позволяет решать задачи по динамике, механике и описывать различные явления в физике, такие как вращение тел и деформация материала.
Таким образом, знание и применение криволинейного движения являются важными компонентами физического образования и позволяют нам лучше понять и объяснить разнообразные явления и процессы в природе и технике.



