Смежные углы - это два угла, которые имеют общую вершину и одну общую сторону. Другими словами, смежные углы расположены рядом друг с другом и имеют общую вершину и сторону, но не пересекаются друг с другом. В геометрии смежные углы часто встречаются при работе с параллельными линиями или на пересечении линий.
Вертикальные углы - это два угла, которые образуются пересечением двух прямых линий. Они расположены напротив друг друга и имеют общую вершину. Вертикальные углы равны между собой и имеют одинаковую меру. Также важно отметить, что вертикальные углы не должны путаться с параллельными углами, которые образуются пересечением параллельных линий и не имеют общей вершины.
Знание основных понятий и свойств смежных и вертикальных углов является важным при изучении геометрии и решении задач. Понимание этих концепций помогает определить соотношения между углами и применять их в решении геометрических задач. Также знание свойств смежных и вертикальных углов может быть полезно при конструировании, настройке и анализе геометрических фигур и объектов.
Понятие смежных углов и их свойства

Смежные углы могут быть различных видов:
- Смежные углы прилежащие - это два угла, которые имеют общую сторону и одну общую вершину, причем они лежат по одну сторону от общей стороны и образуют линию.
- Смежные углы вертикальные - это два угла, которые имеют общую вершину, но стороны этих углов расположены на пересекающихся прямых и направлены в противоположные стороны.
Свойства смежных углов:
- Сумма смежных углов всегда равна 180 градусов.
- Если один из смежных углов является прямым, то другой угол будет также прямым.
- Если один из смежных углов является острым, то другой угол будет тупым.
- Смежные углы, которые имеют общую вершину и лежат по одну сторону от общей стороны, образуют пару углов, дополняющихся до прямого угла (угол, равный 180 градусам).
Знание о понятии смежных углов и их свойствах позволяет производить расчеты и применять их в решении геометрических задач.
Смежные углы: определение и примеры

Основные свойства смежных углов:
- Сумма смежных углов всегда равна 180 градусов.
- Если углы смежные, значит они дополнительные друг к другу. То есть, если сумма смежных углов равна 180 градусов, то каждый из них является дополнением другого.
- Смежные углы имеют общую вершину и общую сторону, но не пересекаются внутри фигуры.
Примеры смежных углов:
На рисунке показаны смежные углы АВС и ВСD. Они имеют общую вершину В и общую сторону ВС.
Свойства смежных углов и их применение

Свойства смежных углов:
| Свойство | Описание |
|---|---|
| Сумма смежных углов | Сумма двух смежных углов всегда составляет 180 градусов. Это следует из того, что угол является частью прямой или полного вращения, которые составляют 180 градусов. |
| Образование пар вертикальных углов | Смежные углы, образуемые пересекающимися прямыми, являются вертикальными углами. Такие углы равны между собой и обозначаются одной буквой, за которой ставятся две точки. |
Применение свойств смежных углов:
Знание свойств смежных углов позволяет решать задачи на построение, нахождение неизвестного угла, доказывать равенство углов и многое другое. Например, если известны значения одного из смежных углов и сумма смежных углов, можно определить значение другого смежного угла.
Смежные углы являются важными элементами в геометрии и находят широкое применение в решении задач различной сложности.
Понятие вертикальных углов и их свойства
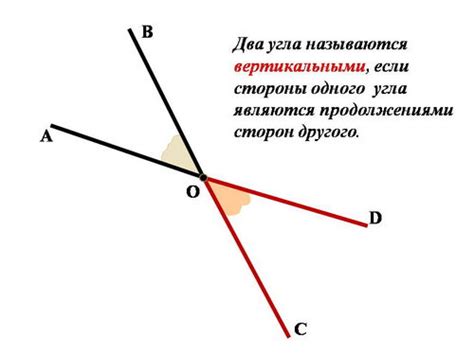
Вертикальные углы определяются взаимной перпендикулярностью двух прямых, которые пересекаются в одной точке. То есть, вертикальные углы образуются параллельными линиями, когда одна из прямых пересекает другую.
Основное свойство вертикальных углов заключается в их равенстве. Если две прямые пересекаются, то вертикальные углы, образованные этими прямыми, будут равными друг другу. Это свойство можно легко доказать, используя теорему о параллельных линиях. Также стоит отметить, что вертикальные углы обладают свойством симметрии: если один из вертикальных углов имеет определенную меру, то другой вертикальный угол также будет иметь ту же меру.
Знание понятия вертикальных углов и их свойств позволяет нам решать различные задачи в геометрии, такие как нахождение углов или доказательство равенства углов. Поэтому понимание вертикальных углов является важным аспектом в изучении геометрии и математики в целом.




