Косинус угла – это математическая функция, определяющая отношение прилежащего катета прямоугольного треугольника к гипотенузе. Значение косинуса угла всегда находится в диапазоне от -1 до 1. Важно понимать, что при значении косинуса равного 0, угол обладает определенными свойствами и играет особую роль в геометрии и тригонометрии.
Когда косинус угла равен нулю, это означает, что прилежащий катет прямоугольного треугольника равен нулю, то есть угол прилегает к гипотенузе. Это является специальным случаем, когда прямоугольный треугольник вырождается в линию. При этом угол становится прямым, и его косинус равен нулю.
Однако, следует отметить, что существуют несколько углов, значения косинуса которых также равны нулю. Например, половинное деление окружности на 4 равные части дает нам 4 угла, по 90 градусов каждый. Во всех этих углах косинус также равен нулю. Эти углы являются кратными прямых углов и называются комульсаками углами.
Косинус угла в геометрии

Косинус угла в геометрии позволяет нам расчитывать различные параметры треугольников, такие как длины сторон, углы между сторонами и площадь треугольника.
Используя косинус угла, мы можем определить угол между двумя векторами в трехмерном пространстве. Это дает нам возможность решать различные геометрические задачи, включая построение проекций векторов и нахождение угла между двумя плоскостями.
Косинус угла также применяется в различных областях науки и техники, например, на физике, астрономии и компьютерной графике. Он используется для моделирования и визуализации объектов в пространстве, определения расстояния между точками и нахождения направления движения.
В целом, косинус угла играет важную роль в геометрии и имеет широкий спектр применений. Понимание его значения и свойств помогает нам решать различные задачи, связанные с изучением геометрии и анализом пространственных объектов.
Определение и значение

Значение косинуса угла может варьироваться от -1 до 1, где -1 означает, что угол является тупым, 1 - прямым, а 0 - прямым углом.
Косинус угла также может быть интерпретирован как мера сходства двух векторов в многомерном пространстве. Если косинус угла между векторами равен 1, это означает, что векторы направлены в одном направлении, а если косинус равен -1, векторы направлены в противоположных направлениях.
В математике косинус угла широко используется для решения геометрических задач, а в физике он играет важную роль при расчетах траекторий движения тел.
Свойства косинуса

Основные свойства косинуса:
- Значения косинуса: косинус угла всегда принимает значения в диапазоне от -1 до 1.
- Углы с равными значениями косинуса: если два угла имеют одинаковые значения косинуса, то эти углы называются сопряженными.
- Угол нулевого косинуса: когда косинус угла равен нулю, это означает, что данный угол равен 90 градусам или кратен 180 градусам.
- Угол единичного косинуса: когда косинус угла равен единице, это означает, что данный угол равен 0 градусам или кратен 360 градусам.
- Угол минимального косинуса: для двух углов, сумма которых равна 180 градусам, сумма их косинусов всегда равна -1.
- Отношение косинуса к синусу: косинус угла делится на синус угла прямоугольного треугольника равно отношению прилежащего катета к гипотенузе.
Знание и использование свойств косинуса позволяет проводить различные вычисления и решать задачи, связанные с геометрией, физикой и другими науками.
Аналитические формулы для вычисления косинуса

Существуют аналитические формулы, которые помогают вычислить косинус угла без необходимости измерять его физически. Ниже приведены некоторые из наиболее часто используемых формул:
| Тип формулы | Формула |
|---|---|
| Теорема Пифагора | \( \cos(\alpha) = \frac{c^2 - a^2 - b^2}{-2ab} \) |
| Формула половинного угла | \( \cos\left(\frac{\theta}{2} ight) = \sqrt{\frac{1 + \cos(\theta)}{2}} \) |
| Формула тройного угла | \( \cos(3\theta) = 4\cos^3(\theta) - 3\cos(\theta) \) |
Эти формулы позволяют вычислить значение косинуса угла в зависимости от известных параметров. Они особенно полезны, когда точные значения углов неизвестны или трудно измерить.
Зная аналитические формулы, вы можете легко вычислить косинус угла и использовать его для решения различных задач и вычислений в математике и физике.
Косинус углов особых значений
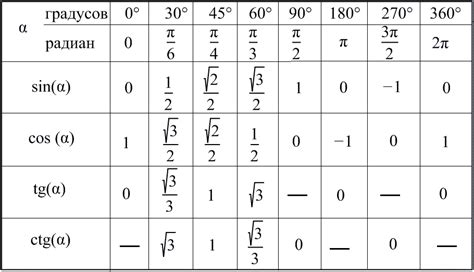
1. Косинус нулевого угла: косинус нулевого угла равен 1. Это означает, что когда два вектора совпадают, косинус угла между ними равен 1.
2. Косинус 90 градусов: косинус 90 градусов равен 0. Это означает, что когда два вектора перпендикулярны друг другу, косинус угла между ними равен 0.
3. Косинус 180 градусов: косинус 180 градусов равен -1. Это означает, что когда два вектора направлены в противоположных направлениях, косинус угла между ними равен -1.
4. Косинус угла больше 180 градусов: косинус угла больше 180 градусов также равен -1. Это связано с тем, что косинус является периодической функцией с периодом 360 градусов.
Таким образом, косинус углов особых значений имеет важное значение в геометрии и тригонометрии, и помогает нам понять отношение между векторами в пространстве.



