Косинус, тангенс, котангенс, синус - это тригонометрические функции, которые широко используются в математике, физике и других науках. Они отображают соотношение между углом двух сторон правильного треугольника и позволяют определить значения этих функций для любого угла.
Косинус (cos) - это отношение прилежащего катета к гипотенузе треугольника. Значение косинуса может быть от -1 до 1. Если угол равен 0, косинус будет равен 1, а если угол равен 90 градусам, косинус будет равен 0.
Тангенс (tan) - это отношение противолежащего катета к прилежащему катету треугольника. Значение тангенса может быть любым числом, включая бесконечность и минус бесконечность. Если угол равен 0, тангенс будет равен 0.
Котангенс (ctg) - это обратная функция к тангенсу, то есть отношение прилежащего катета к противолежащему. Значение котангенса также может быть любым числом. Если угол равен 0, котангенс будет равен бесконечности.
Синус (sin) - это отношение противолежащего катета к гипотенузе треугольника. Значение синуса также может быть от -1 до 1. Если угол равен 0, синус будет равен 0, а если угол равен 90 градусам, синус будет равен 1.
Ниже приведена таблица со значениями косинуса, тангенса, котангенса и синуса для некоторых углов:
Косинус, тангенс, котангенс, синус: таблица и значения Русский язык
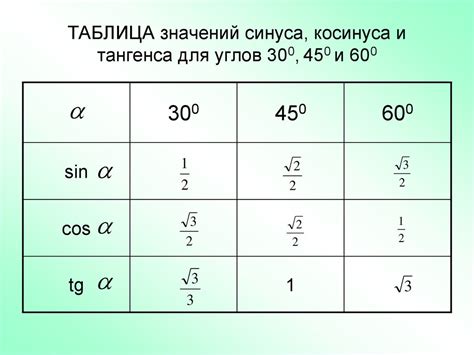
Косинус, тангенс и котангенс являются отношениями двух сторон прямоугольного треугольника, а синус представляет собой отношение противолежащего катета к гипотенузе.
Значения косинуса, тангенса, котангенса и синуса зависят от угла, измеряемого в радианах или градусах. Обычно эти значения представлены в виде таблиц, где указаны соответствующие значения функций для различных углов.
В таблице можно найти значения косинуса, тангенса, котангенса и синуса для углов от 0 до 90 градусов или от 0 до π/2 радиан.
Примеры значений тригонометрических функций:
| Угол (градусы) | Угол (радианы) | Косинус | Тангенс | Котангенс | Синус |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | ∞ | 0 |
| 30 | π/6 | √3/2 | √3 | 1/√3 | 1/2 |
| 45 | π/4 | 1/√2 | 1 | 1 | 1/√2 |
| 60 | π/3 | 1/2 | √3/2 | √3/√3 | √3/2 |
| 90 | π/2 | 0 | ∞ | 0 | 1 |
Зная значения этих функций, можно решать различные задачи, связанные с геометрией, механикой, физикой и другими научными областями.
Таблица значений косинуса, тангенса, котангенса и синуса
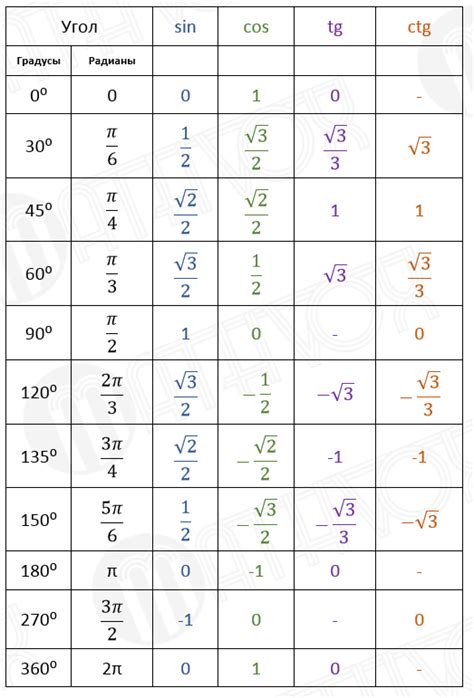
В данной таблице представлены значения косинуса (cos), тангенса (tan), котангенса (cot) и синуса (sin) для углов в градусах:
| Угол | Косинус (cos) | Тангенс (tan) | Котангенс (cot) | Синус (sin) |
|---|---|---|---|---|
| 0° | 1 | 0 | ∞ | 0 |
| 30° | √3/2 | √3 | 1/√3 | 1/2 |
| 45° | √2/2 | 1 | 1 | √2/2 |
| 60° | 1/2 | √3/3 | √3 | √3/2 |
| 90° | 0 | ∞ | 0 | 1 |
| 180° | -1 | 0 | ∞ | 0 |
| 270° | 0 | ∞ | 0 | -1 |
| 360° | 1 | 0 | ∞ | 0 |
Значения градусов могут быть преобразованы в радианы, умножив их на π/180.
Значение косинуса, тангенса, котангенса и синуса в математике

Значения косинуса, тангенса, котангенса и синуса в таблице могут быть представлены в виде:
- Косинус (cos):
- 0°: 1
- 30°: √3/2
- 45°: √2/2
- 60°: 1/2
- 90°: 0
- Синус (sin):
- 0°: 0
- 30°: 1/2
- 45°: √2/2
- 60°: √3/2
- 90°: 1
- Тангенс (tan):
- 0°: 0
- 30°: √3/3
- 45°: 1
- 60°: √3
- 90°: не существует
- Котангенс (cot):
- 0°: не существует
- 30°: √3
- 45°: 1
- 60°: √3/3
- 90°: 0
Значения этих функций могут быть использованы для нахождения неизвестных сторон и углов в треугольнике или для решения задач физики, геометрии и других научных дисциплин.
Как получить значения косинуса, тангенса, котангенса и синуса для угла
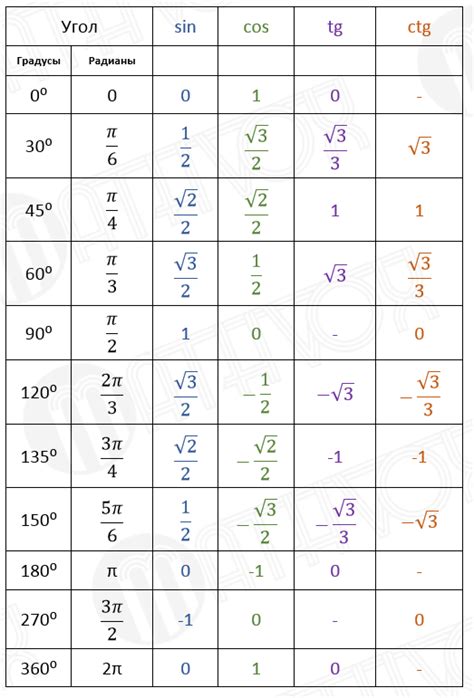
Значения косинуса, тангенса, котангенса и синуса для угла можно получить с помощью таблицы значений или с использованием математических формул. В таблице представлены основные значения для углов от 0 до 90 градусов.
Таблица значений:
- Угол 0°: косинус (cos) = 1, синус (sin) = 0, тангенс (tan) = 0, котангенс (cot) = не определен;
- Угол 30°: косинус (cos) = \(\frac{\sqrt{3}}{2}\), синус (sin) = \(\frac{1}{2}\), тангенс (tan) = \(\frac{\sqrt{3}}{3}\), котангенс (cot) = \(\sqrt{3}\);
- Угол 45°: косинус (cos) = \(\frac{\sqrt{2}}{2}\), синус (sin) = \(\frac{\sqrt{2}}{2}\), тангенс (tan) = 1, котангенс (cot) = 1;
- Угол 60°: косинус (cos) = \(\frac{1}{2}\), синус (sin) = \(\frac{\sqrt{3}}{2}\), тангенс (tan) = \(\sqrt{3}\), котангенс (cot) = \(\frac{1}{\sqrt{3}}\);
- Угол 90°: косинус (cos) = 0, синус (sin) = 1, тангенс (tan) = не определен, котангенс (cot) = 0.
Для получения значений косинуса, тангенса, котангенса и синуса для других углов можно использовать математические формулы и тригонометрические соотношения. Например, косинус угла можно вычислить с помощью функции cos(x), где x - значение угла в радианах.
Отношения синуса и косинуса определяются по формуле: sin(x) = \(\frac{opposite}{hypotenuse}\), cos(x) = \(\frac{adjacent}{hypotenuse}\), где opposite - противолежащий катет, adjacent - прилежащий катет, hypotenuse - гипотенуза прямоугольного треугольника.
Значения тангенса и котангенса также определяются через синус и косинус: tan(x) = \(\frac{sin(x)}{cos(x)}\), cot(x) = \(\frac{cos(x)}{sin(x)}\).
Применение косинуса, тангенса, котангенса и синуса в русском языке

Например, значение косинуса может быть использовано для описания угла наклона или направления движения. Если мы говорим о ком-то, что он "идет под углом к оси X", то это может означать, что его движение не прямолинейно, а имеет определенное отклонение, подобно косинусу. Тангенс и котангенс также используются для описания углов и направлений, но в других контекстах.
Синус часто используется для описания колебаний, волн и ритмов. Если мы говорим о человеке или музыкальном инструменте, что он "выдающийся синусоидальный сигнал", то это означает, что он способен производить гармоничные и ритмичные звуки.
Косинус, тангенс, котангенс и синус также имеют свое место в различных выражениях и пословицах. Например, выражение "мой косинус с тобой - нуль" может означать, что мы не сходимся во мнении или не понимаем друг друга. А выражение "у него котангенс - бесконечность" может описывать необычные или экстремальные характеристики человека или ситуации.
Таким образом, косинус, тангенс, котангенс и синус нашли свое применение не только в математике и физике, но и в русском языке. Их значения и свойства используются для описания различных явлений и характеристик, а также в различных выражениях и пословицах.
Как использовать таблицу значений косинуса, тангенса, котангенса и синуса
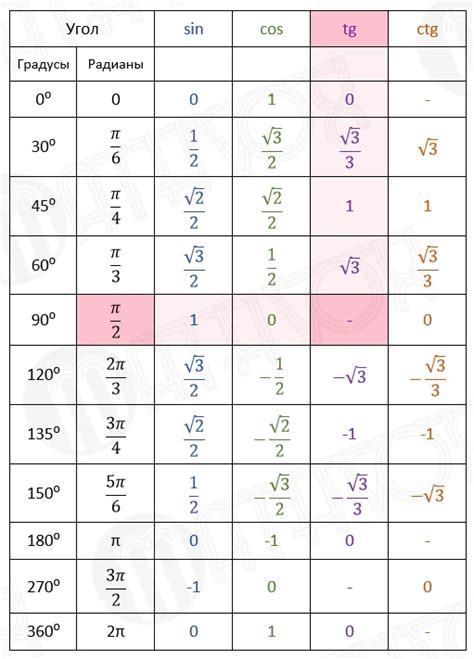
Для использования таблицы значений необходимо знать значение угла, для которого вы хотите найти косинус, тангенс, котангенс или синус. В таблице значения представлены для различных углов в градусах.
Пример использования таблицы:
| Угол (градусы) | Косинус | Тангенс | Котангенс | Синус |
|---|---|---|---|---|
| 0° | 1 | 0 | ∞ | 0 |
| 30° | √3/2 | √3 | 1/√3 | 1/2 |
| 45° | 1/√2 | 1 | 1 | 1/√2 |
| 60° | 1/2 | √3/3 | √3 | √3/2 |
| 90° | 0 | ∞ | 0 | 1 |
Найдите в таблице значение косинуса, тангенса, котангенса или синуса для нужного вам угла и используйте его в своих вычислениях или задачах.
Зная значения этих функций для различных углов, вы можете с легкостью проводить математические расчеты, решать задачи или применять их в научных и инженерных вычислениях.



