Косинус 0.75 — простой способ нахождения угла и его применение в математике и физике

Углы являются одним из основных понятий геометрии, и они играют важную роль во многих научных и инженерных областях.

Одним из способов определения угла является его тригонометрическая функция - косинус.

Если известно значение косинуса угла, то можно найти сам угол. В данной статье мы рассмотрим, как найти угол, если косинус равен 0.75.

Косинус угла определяется как отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.

Он может принимать значения от -1 до 1.

В данном случае, косинус равен 0.75, что говорит о том, что прилежащий катет составляет 0.75 от длины гипотенузы.

Чтобы найти угол, соответствующий данному значению косинуса, необходимо воспользоваться обратной функцией - арккосинусом.

На многих научных калькуляторах это обозначается как cos^-1.

В нашем случае, арккосинус 0.75 равен примерно 41.41 градусов.

Таким образом, угол, соответствующий косинусу 0.75, составляет приблизительно 41.41 градусов.

Этот метод нахождения угла может быть полезен при решении различных задач, связанных с треугольниками и применением тригонометрии.

Неравенство треугольника и его применение при поиске углов

Это неравенство можно использовать для нахождения углов треугольника, основываясь на известных значениях сторон и косинусов противоположных углов. В данной задаче, косинус угла равен 0.75, что означает, что смежные стороны угла имеют отношение 3:4.

Зная это, мы можем использовать неравенство треугольника, чтобы найти остальные углы треугольника. Например, если сторона A соответствует углу A, а сторона B соответствует углу B, то сумма углов треугольника будет равна 180 градусам:

Угол A + Угол B + Угол C = 180°

Таким образом, если мы знаем угол A и угол B, мы можем найти угол C, вычитая сумму углов A и B из 180 градусов. Используя известные значения углов, мы можем решить данную задачу и найти отсутствующий угол треугольника.

Примечание: При решении задачи важно помнить, что неравенство треугольника работает только для невырожденных треугольников, то есть треугольников, у которых каждая сторона больше 0.

Определение косинуса угла, его значения от 0 до 1

Если косинус угла равен 0.75, это означает, что отношение прилегающей катеты к гипотенузе равно 0.75. Для определения самого угла можно использовать обратную функцию косинуса - арккосинус (cos^-1 или arccos). Применив арккосинус к значению 0.75, мы найдем значение угла.

В данном случае, если cos^-1(0.75) ≈ 0.7227 радиан или около 41.41 градусов. Это означает, что угол, косинус которого равен 0.75, примерно равен 41.41 градусам.

Расчет значения косинуса угла по формуле

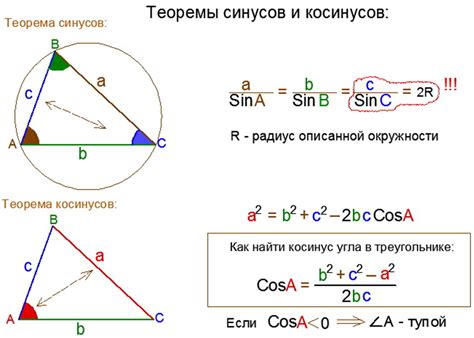
Для расчета значения косинуса угла можно использовать следующую формулу:

• Угол, для которого мы хотим найти значение косинуса, обозначим как α.
• Известное значение косинуса угла α обозначим как cos(α).
• Находим объемлющий прямоугольный треугольник, у которого катет, примыкающий к углу α, равен 1 (это возможно, так как косинус угла принимает значения от -1 до 1).
• Находим гипотенузу треугольника заданного косинуса, используя теорему Пифагора: гипотенуза в квадрате равна сумме квадратов катетов; в нашем случае один из катетов равен 1.
• Находим гипотенузу треугольника: гипотенуза = sqrt(1^2 - cos(α)^2).

Таким образом, значение косинуса угла α может быть найдено путем подстановки известного значения и решения уравнения для гипотенузы.

Решение уравнения для нахождения угла с заданным косинусом

Уравнение для нахождения угла с заданным косинусом выглядит следующим образом:

cos(x) = 0.75

Чтобы найти угол x, нужно применить арккосинус к обоим частям уравнения:

x = arccos(0.75)

Подставляя значение косинуса, мы получаем:

x = arccos(0.75) ≈ 0.7227 радиан

Таким образом, угол x, косинус которого равен 0.75, составляет примерно 0.7227 радиан.

Пример нахождения угла с косинусом 0,75

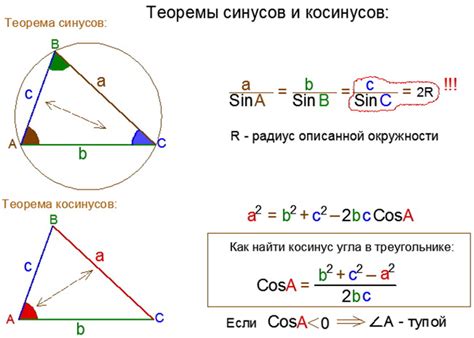
Чтобы найти угол, если его косинус равен 0,75, можно воспользоваться обратной функцией косинуса, называемой арккосинусом.

Математический символ арккосинуса обозначается как acos(). Если передать в функцию значение 0,75, она вернет значение угла в радианах. Чтобы получить значение угла в градусах, необходимо умножить результат на 180 и разделить на π.

В данном случае, чтобы найти угол, подставим значение 0,75 в функцию арккосинуса:

Результатом будет угол в радианах. Чтобы получить значение угла в градусах, нужно выполнить следующее вычисление:

Таким образом, для косинуса 0,75 угол будет равен примерно 41,41 градусов.

Связь значения косинуса угла и его направления

Когда косинус угла равен 1, это означает, что угол равен 0 градусов. При этом катет совпадает с гипотенузой, и треугольник является вырожденным - прямой линией.

В случае, когда косинус угла равен 0, это означает, что катет перпендикулярен гипотенузе. Угол в таком случае составляет 90 градусов, и треугольник является прямоугольным.

Если косинус угла меньше 0, то значит, что косинус отрезан от синуса вертикальной осью. Это значит, что угол находится в третьем или четвертом квадранте, где значения косинуса отрицательны.

В случае, когда косинус угла больше 0, это означает, что косинус расположен в положительном полуплоскости оси абсцисс. Такие углы находятся в первом или втором квадранте, где значения косинуса положительны.

Используя значение косинуса угла равного 0.75, можно определить его направление и узнать, что угол находится в первом квадранте. Относительно начальной оси (оси абсцисс), угол будет располагаться в положительном направлении.

Заданное значение косинуса, равное 0.75, позволяет нам определить возможные углы, для которых значение косинуса будет равно этой величине.

Косинус угла является отношением прилежащего катета и гипотенузы в треугольнике. Используя это определение и значение косинуса, мы можем найти соответствующий угол.

Таким образом, угол, для которого косинус равен 0.75, может быть найден с помощью обратного косинуса (арккосинуса) от данного значения. В данном случае, арккосинус от 0.75 равен примерно 41.4096 градусов.

С другой стороны, косинус является периодической функцией с периодом 360 градусов, поэтому существует бесконечное множество углов, для которых косинус равен 0.75. Они могут быть найдены путем добавления или вычитания кратного периода 360 градусов от найденного угла.

Таким образом, возможные значения угла при заданном значении косинуса 0.75 будут:

Угол 1: 41.4096 градусов

Угол 2: 41.4096 + 360 = 401.4096 градусов

Угол 3: 41.4096 - 360 = -318.5904 градусов

Эти значения представляют основные возможные углы с косинусом 0.75. Однако, можно найти и другие значения, добавляя или вычитая кратное периода 360 градусов.