Косинус и синус являются двумя основными тригонометрическими функциями, которые широко используются в математике и физике. Они связаны с геометрией и позволяют изучать различные свойства и закономерности, касающиеся углов и соотношений между сторонами треугольников.
Косинус угла равен отношению длины прилежащего катета к длине гипотенузы прямоугольного треугольника. Изучение значений косинуса позволяет определить, какую часть гипотенузы составляет прилежащий катет при данном угле.
Синус угла определяется как отношение длины противоположного катета к длине гипотенузы прямоугольного треугольника. Он также позволяет определить, какую часть гипотенузы составляет противоположный катет при данном угле.
Отношение косинуса к синусу называется тангенсом. Тангенс угла равен отношению синуса к косинусу этого угла. Величина тангенса позволяет определить, насколько при вращении объекта относительно начальной точки его вертикальная координата будет меняться по сравнению с горизонтальной координатой.
Что такое косинус и синус?
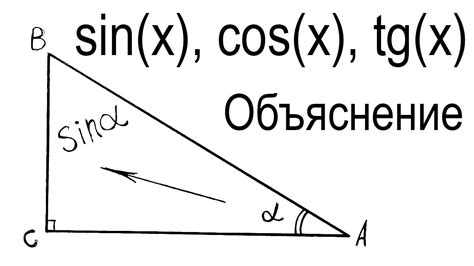
Косинус и синус определяются для любых вещественных чисел и измеряются в радианах.
Косинус (cos) угла – это отношение длины прилегающего катета прямоугольного треугольника к гипотенузе этого треугольника. Косинус угла также можно интерпретировать как абсциссу точки на единичной окружности, образующей данный угол с положительной полуосью оси абсцисс.
Синус (sin) угла – это отношение длины противолежащего катета прямоугольного треугольника к гипотенузе этого треугольника. Синус угла также можно интерпретировать как ординату точки на единичной окружности, образующей данный угол с положительной полуосью оси абсцисс.
Косинус и синус связаны между собой соотношением, которое называется тригонометрическим тождеством:
cos^2α + sin^2α = 1
Это соотношение позволяет выразить одну тригонометрическую функцию через другую и использовать их вместе для решения различных математических задач.
Определение и основные свойства

Синус также является тригонометрической функцией, которая определяется отношением противоположного катета прямоугольного треугольника к гипотенузе. Синус применяется для нахождения углов по их синусам и в различных математических и физических задачах.
Косинус 0.6 обозначает значение косинуса угла, равного 0.6 радиан или примерно 34.38 градусов. Косинус 0.6 является численным значением равным отношению длины прилежащего катета к длине гипотенузы в прямоугольном треугольнике с углом 0.6 радиан.
Основные свойства косинуса и синуса:
- Периодичность: Косинус и синус являются периодическими функциями с периодом 2π (или 360 градусов), то есть значения функций повторяются каждые 2π радиан (или 360 градусов).
- Значения функций: Косинус и синус могут принимать значения от -1 до 1. Косинус 0 равен 1, а синус 0 равен 0.
- Ортогональность: Косинус и синус ортогональны друг другу. Это означает, что скалярное произведение косинуса и синуса равно нулю.
Знание косинуса и синуса имеет значение во многих областях, включая математику, физику, инженерию и компьютерную графику. Они используются для решения уравнений, моделирования движения, анализа сигналов и других задач.
Геометрическая интерпретация
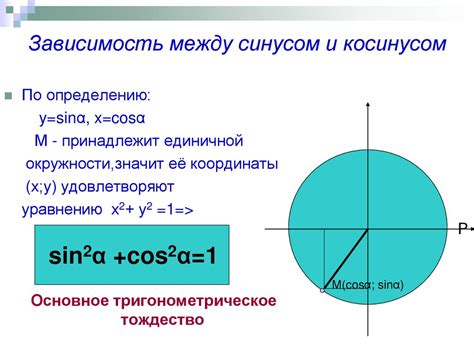
Геометрическая интерпретация косинуса и синуса заключается в следующем:
Пусть у нас есть прямоугольный треугольник со сторонами a, b и гипотенузой c. Угол между стороной a и гипотенузой c обозначим α.
Тогда косинус угла α равен отношению длины катета a к длине гипотенузы c, то есть cos(α) = a / c.
А синус угла α равен отношению длины катета b к длине гипотенузы c, то есть sin(α) = b / c.
Таким образом, косинус угла представляет собой отношение прилежащего катета к гипотенузе, а синус угла - отношение противоположного катета к гипотенузе треугольника.
Соотношение между косинусом и синусом угла определяется теоремой Пифагора. Согласно этой теореме, сумма квадратов длин катетов треугольника равна квадрату длины гипотенузы, то есть a^2 + b^2 = c^2.
Отношение катетов к гипотенузе возводится в квадрат и складывается, а затем извлекается корень: cos^2(α) + sin^2(α) = 1.
Это соотношение известно как тригонометрическое тождество, которое является основной формулой тригонометрии.
Соотношение между косинусом и синусом
Косинус угла определяется как отношение прилежащего катета к гипотенузе в прямоугольном треугольнике. Синус угла, в свою очередь, равен отношению противоположного катета к гипотенузе. Обозначения для косинуса и синуса соответственно - cos и sin.
Соотношение между косинусом и синусом выражается через треугольник на единичной окружности. Сумма квадратов косинуса и синуса угла всегда равна единице: cos^2(α) + sin^2(α) = 1.
Это соотношение, известное как тригонометрическое тождество, следует из теоремы Пифагора и является фундаментальным свойством косинуса и синуса. Оно позволяет нам вычислять одну функцию, зная значение другой, и использовать их в различных прикладных задачах.
Тригонометрическая формула

Косинус (cos) и синус (sin) являются функциями, которые определены для всех действительных чисел. Косинус выражает отношение длины прилегающего катета к длине гипотенузы прямоугольного треугольника, а синус - отношение длины противоположного катета к длине гипотенузы.
Тригонометрическая формула связывает косинус и синус следующим образом:
cos^2(x) + sin^2(x) = 1
Эта формула справедлива для любого значения x. Она является основой для многих других тригонометрических и геометрических выкладок и связей.



