В современном мире многие явления и процессы связаны между собой, и понимание природы этих связей является важной задачей для научного исследования. Одним из способов определения связи между двумя явлениями является анализ корреляции. Корреляция – это числовой показатель, который позволяет оценить степень взаимосвязи между двумя переменными. Методы определения корреляции используются во множестве научных областей, включая статистику, психологию, экономику, медицину и другие.
Одним из основных принципов определения корреляции является сбор и анализ данных. Для этого необходимо получить информацию о значениях двух переменных, которые мы хотим сравнить. Например, если мы хотим узнать, есть ли связь между количеством часов, которые студенты тратят на учебу, и их академической успеваемостью, мы должны провести опрос и получить данные о количестве часов, которые студенты тратят на учебу, и о их оценках.
После сбора данных можно приступать к анализу корреляции. Существуют разные методы для определения корреляции, но одним из наиболее распространенных является метод Пирсона. Метод Пирсона позволяет измерить линейную связь между двумя переменными. В результате анализа получается коэффициент корреляции, который принимает значения от -1 до 1. Значение коэффициента корреляции ближе к -1 или 1 указывает на сильную связь между переменными, а значение ближе к 0 указывает на слабую или отсутствующую связь.
Корреляция может быть положительной, когда две переменные движутся в одном направлении (увеличение одной переменной сопровождается увеличением другой), или отрицательной, когда две переменные движутся в противоположных направлениях (увеличение одной переменной сопровождается уменьшением другой). Значение коэффициента корреляции позволяет определить не только наличие связи между явлениями, но и ее направление и силу.
Что такое корреляция
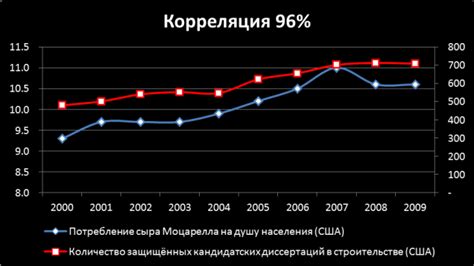
Значение корреляции находится в диапазоне от -1 до 1. Если корреляция равна 1, это означает полную прямую зависимость между переменными. Если же корреляция равна -1, это указывает на полную обратную зависимость. Значение близкое к нулю указывает на отсутствие связи между переменными.
Для определения корреляции между переменными используется коэффициент корреляции. Наиболее распространенный коэффициент корреляции - это коэффициент Пирсона. Он измеряет линейную связь между двумя переменными и может принимать значения от -1 до 1.
| Значение коэффициента Пирсона | Степень корреляции |
|---|---|
| 0 | Очень слабая или отсутствующая корреляция |
| 0 - 0,3 | Слабая положительная или отрицательная корреляция |
| 0,3 - 0,7 | Умеренная положительная или отрицательная корреляция |
| 0,7 - 1 | Сильная положительная или отрицательная корреляция |
Корреляция полезна для определения связи между различными переменными и позволяет выявить закономерности и тенденции. Она используется в различных областях, включая экономику, психологию, медицину и другие науки.
Определение и основные понятия

Основными понятиями при изучении корреляции являются:
- Коэффициент корреляции – числовая мера, описывающая степень линейной связи между двумя переменными. Коэффициент корреляции принимает значения от -1 до 1. Значение 1 означает положительную линейную связь, значение -1 – отрицательную линейную связь, а значение 0 – отсутствие связи.
- Корреляционная матрица – таблица, в которой значениями являются коэффициенты корреляции между переменными. Корреляционная матрица позволяет визуально оценить взаимосвязи между переменными.
- Статистическая значимость – показатель, определяющий, насколько вероятно то, что наблюдаемая корреляция является случайной. Статистическая значимость позволяет оценить достоверность полученных результатов и их применимость к генеральной совокупности.
Использование принципов и методов определения корреляции позволяет выявлять и изучать связь между явлениями, что является важным инструментом в различных областях знания, таких как социология, экономика, медицина и другие.
Методы измерения корреляции

2. Коэффициент корреляции Спирмена. Данный метод также оценивает связь между переменными, но не требует линейности этой связи. Вместо этого он основывается на рангах значений переменных. Коэффициент корреляции Спирмена, обозначаемый как ρ, может принимать значения от -1 до 1. Он также позволяет определить тип и силу связи между переменными.
3. Коэффициент корреляции Кендалла. Этот метод также основывается на рангах значений переменных, но в отличие от коэффициента Спирмена, он учитывает пару значений и их порядок. Коэффициент корреляции Кендалла, обозначаемый как τ, также может принимать значения от -1 до 1. Он позволяет определить силу и направление связи между переменными.
4. Коэффициент детерминации. Данный метод позволяет оценить, насколько одна переменная может быть предсказана по другой. Коэффициент детерминации, обозначаемый как R², может принимать значения от 0 до 1. Значение R² близкое к 1 указывает на то, что одна переменная хорошо предсказывается по другой, а значение близкое к 0 - на отсутствие предсказательной силы.
Коэффициент Пирсона

Коэффициент Пирсона вычисляется путем деления ковариации двух переменных на произведение их стандартных отклонений. Он принимает значения от -1 до 1, где -1 означает полную отрицательную корреляцию, 0 – отсутствие корреляции и 1 – положительную корреляцию.
Для вычисления коэффициента Пирсона необходимо иметь значения двух переменных для каждого наблюдения. Затем осуществляется расчет ковариации, которая измеряет направление и силу линейной связи между переменными. Ковариация равна среднему значению произведения отклонений значений переменных от их средних. Затем вычисляются стандартные отклонения каждой переменной. Финальный результат получают путем деления ковариации на произведение стандартных отклонений.
Коэффициент Пирсона позволяет определить, насколько две переменные взаимосвязаны и в какой степени они влияют друг на друга. Величина коэффициента позволяет оценить силу связи между переменными, а его знак указывает направление связи: положительное или отрицательное.
Преимуществами коэффициента Пирсона являются его простота и широкое использование. Он позволяет определить наличие линейной связи между переменными, что является важным во многих областях науки и бизнесе. Однако коэффициент Пирсона не способен выявлять нелинейные связи и устойчив к выбросам. Кроме того, он может быть неприменим в случае наличия категориальных переменных или отсутствия нормального распределения данных.
Коэффициент Спирмена

Для расчета коэффициента Спирмена необходимо присвоить каждому значению каждой переменной ранг, отсортировав их по возрастанию. Затем посчитывается разность рангов для каждой пары значений и рассчитывается значение коэффициента.
Значение коэффициента Спирмена может быть в диапазоне от -1 до 1. Значение близкое к 1 свидетельствует об уклоне к прямой положительной корреляции, а значение близкое к -1 указывает на уклон к прямой отрицательной корреляции. Значение близкое к нулю говорит о слабой или отсутствующей связи между переменными.
Коэффициент Спирмена позволяет оценить не только линейную связь между переменными, но и любую другую монотонную зависимость. Это делает его предпочтительным методом, когда данные не подчиняются нормальному распределению или когда связь между переменными не является линейной.
Коэффициент Кендалла

Для вычисления коэффициента Кендалла необходимо отсортировать значения каждой переменной по возрастанию ранга, затем сравнить пары значений и посчитать количество согласованных и несогласованных пар. Затем вычисляется статистика, которая принимает значения от -1 до 1. Значение 1 означает идеальную положительную корреляцию, -1 – идеальную отрицательную корреляцию, а 0 – отсутствие корреляции.
Коэффициент Кендалла имеет ряд преимуществ перед другими методами определения корреляции. Во-первых, он устойчив к выбросам, то есть небольшие изменения в данных не окажут значительного влияния на результат. Во-вторых, этот коэффициент можно использовать для выявления не только линейной корреляции, но и других видов зависимостей между переменными.
Однако коэффициент Кендалла имеет свои ограничения. Он требует больше вычислительных ресурсов и времени при обработке больших объемов данных. Также этот коэффициент может не дать точного результата, если данные имеют нестандартные распределения или имеют пропуски.
Принципы анализа корреляции

Для определения связи или корреляции между явлениями используются различные методы и принципы анализа. Вот основные из них:
- Коэффициент корреляции - это статистическая мера, которая позволяет определить, насколько две переменные связаны друг с другом. Коэффициент корреляции может быть положительным, отрицательным или равным нулю, что указывает на степень и направление связи.
- Диаграмма рассеяния - это графическое представление данных, которое помогает визуализировать отношение между двумя переменными. Диаграмма позволяет увидеть, как изменяется одна переменная в зависимости от другой, и выявить наличие или отсутствие связи.
- Тестирование гипотезы - это метод, позволяющий проверить статистическую значимость связи или корреляции между переменными. На основе статистических данных можно принять или отвергнуть гипотезу о наличии или отсутствии связи.
- Интерпретация коэффициента корреляции - для анализа корреляции важно уметь интерпретировать значения коэффициента. Коэффициент корреляции близкий к 1 или -1 указывает на сильную связь между переменными, значения близкие к 0 - на отсутствие связи, а значения близкие к 0.5 или -0.5 - на слабую связь.
- Учет внешних факторов - при анализе корреляции необходимо учитывать влияние внешних факторов, которые могут искажать результаты. Например, если две переменные имеют корреляцию, но при этом влияют на них третьи переменные, то связь между ними может быть некорректной.
С использованием этих принципов и методов анализа корреляции можно более точно определить связь между явлениями и использовать эту информацию для принятия решений в различных областях, например в научных исследованиях, бизнесе или медицине.
Выборка и исследуемые данные

Исследуемые данные могут быть различной природы в зависимости от конкретной задачи. Это могут быть числовые данные, такие как статистические показатели или результаты измерений, или категориальные данные, представленные номинальными или порядковыми переменными.
Для проведения анализа корреляции важно, чтобы исследуемые данные были доступны в достаточном объеме и имели достаточную дисперсию. Это позволит выявить статистически значимую связь между явлениями и получить надежные результаты исследования.



