Параллелограмм - это четырехугольник, все стороны которого параллельны по парам. Он имеет несколько интересных свойств, одно из которых - равенство противоположных сторон и параллельность этих сторон.
Изучение координат точек в параллелограмме позволяет решать различные задачи, связанные с геометрией. Особенно интересно находить координаты точек, если известны координаты других точек параллелограмма.
Пусть 𝑎 (𝑥₁, 𝑦₁), 𝑏 (𝑥₂, 𝑦₂), 𝑐 (𝑥₃, 𝑦₃) - вершины параллелограмма 𝐴𝐵𝐶𝐷 соответственно. Тогда для нахождения координат точки 𝑑 (𝑥₄, 𝑦₄) в параллелограмме мы можем воспользоваться следующими соотношениями:
𝑥₄ = 𝑥₁ + 𝑥₃ - 𝑥₂
𝑦₄ = 𝑦₁ + 𝑦₃ - 𝑦₂
Таким образом, если у нас известны координаты трех вершин параллелограмма, мы можем легко найти координаты четвертой вершины. Это может быть полезно, например, при решении задач по физике или применении геометрии в программировании.
Определение параллелограмма
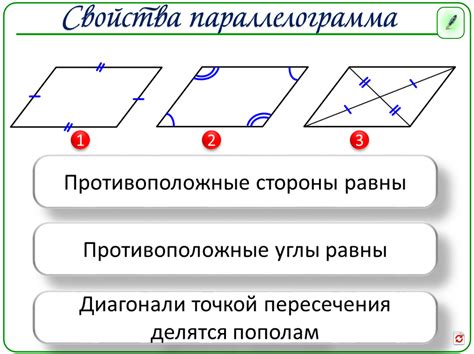
- Все углы параллелограмма равны между собой.
- Сумма противоположных углов параллелограмма равна 180 градусов.
- Диагонали параллелограмма делятся пополам.
- Сумма длин двух диагоналей равна.
Из определения следует, что параллелограмм является особым случаем трапеции, у которой все стороны параллельны друг другу. Параллелограммы встречаются во многих областях, в том числе в геометрии, физике, архитектуре и дизайне.
Свойства параллелограмма
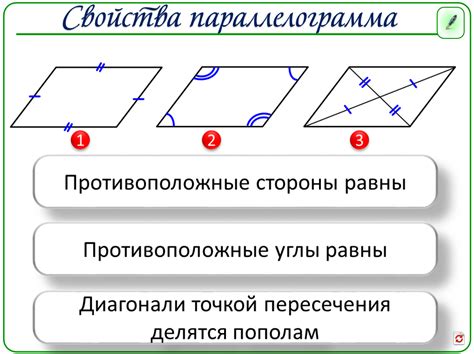
Стороны и углы:
- Противоположные стороны параллельны и равны
- Противоположные углы параллельны и равны
- Смежные углы дополнительны, то есть их сумма равна 180 градусов
Диагонали:
- Диагонали параллелограмма делят его на две равные и подобные фигуры
- Диагонали параллелограмма пересекаются в точке, которая делит каждую диагональ пополам
Симметрия:
- Перпендикуляры, проведенные к противоположным сторонам, пересекаются в серединах этих сторон
- Параллельные противоположные стороны лежат на одной прямой, называемой осью параллелограмма
Координаты точки 𝑑
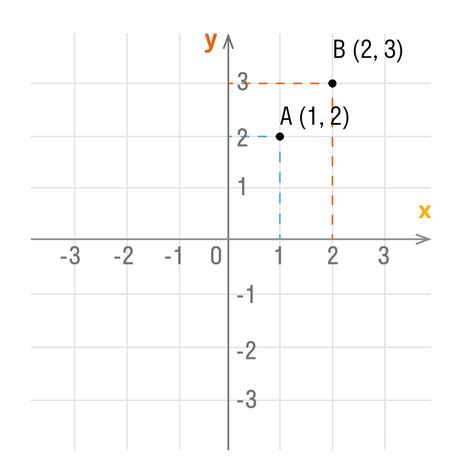
В параллелограмме 𝑨𝑩𝑪𝑫 координаты точки 𝑑 можно вычислить с помощью следующих формул:
- Найдем координаты точки 𝐶, которая находится в середине отрезка 𝐴𝐵. Для этого сложим координаты точек 𝐴 и 𝐵 и поделим полученную сумму на 2. Получим координаты точки 𝐶:
- 𝑪𝑿 = (𝑨𝑿 + 𝑩𝑿) / 2
- 𝑪𝒀 = (𝑨𝒀 + 𝑩𝒀) / 2
- 𝑹𝑿 = 𝑩𝑿 - 𝑨𝑿
- 𝑹𝒀 = 𝑩𝒀 - 𝑨𝒀
- 𝑫𝑿 = 𝑪𝑿 + 𝑹𝑿
- 𝑫𝒀 = 𝑪𝒀 + 𝑹𝒀
Таким образом, мы найдем координаты точки 𝑑 в параллелограмме 𝑨𝑩𝑪𝑫.
Пример решения

Для нахождения координат точки 𝑑 в параллелограмме 𝑎𝑏𝑐𝑑, можно воспользоваться свойствами параллелограмма.
Пусть точка 𝑑 имеет координаты (𝑥, 𝑦). Так как 𝑎𝑏 и 𝑐𝑑 – параллельные стороны параллелограмма, то 𝑑𝑐 параллельно оси 𝑥, а значит, координата 𝑑𝑐 равна координате 𝑐 (𝑥, 𝑦𝑐 = 𝑥).
Также известно, что 𝑎𝑏 и 𝑏𝑐 – равны, а значит, координата 𝑏 равна разности координат 𝑎 и 𝑐 (𝑥𝑎 − 𝑥𝑐 = 𝑦).
Из этих двух равенств можно составить систему уравнений:
{
𝑦 = 𝑥 - 𝑥𝑐,
𝑦 + 𝑦1 = 𝑦2,
}
Где координаты 𝑎 = (𝑥𝑎, 𝑦1) и 𝑐 = (𝑥𝑐, 0), а координата 𝑏 = (𝑥𝑏, 𝑦2) – искомая координата.
Решая эту систему, можно найти значения координат 𝑟.



