Геометрия треугольника – одна из основных разделов математики, которая изучает фигуру, образованную тремя отрезками, соединяющими три точки, не лежащие на одной прямой. В геометрии треугольника существуют различные понятия и определения, одно из которых – катет.
Катет – это одна из сторон прямоугольного треугольника, расположенная под прямым углом. В прямоугольном треугольнике можно найти два катета: прилежащий и противолежащий. Прилежащий катет расположен рядом с углом, из которого проведена высота, а противолежащий – напротив прямого угла.
Катеты являются важными элементами прямоугольного треугольника и играют важную роль при решении различных задач и заданий по геометрии. Они применяются для нахождения площадей, длин, углов и других параметров треугольников, а также во множестве задач с физики, механики и других наук.
Катет в геометрии треугольника: основные понятия
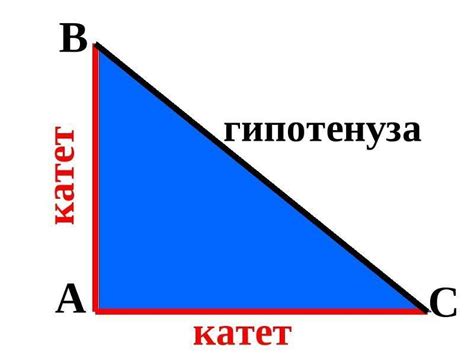
В геометрии треугольника одна из сторон, соединяющих вершины, называется катетом. Катеты образуют прямой угол в прямоугольном треугольнике, а в общем случае могут иметь разные длины и углы. Катеты применяются для решения различных задач и научных исследований.
Каждый треугольник имеет два катета. В прямоугольном треугольнике катеты называются прямыми, так как соединяют вершину прямого угла с остальными вершинами. Один катет лежит рядом с углом прямого угла, а другой – напротив.
Катеты имеют важное значение в оценке длины и углов треугольника. Они могут быть использованы для вычисления площади треугольника, нахождения гипотенузы или других свойств треугольника. Поэтому понимание и применение катетов является существенным аспектом геометрического изучения треугольников.
| Вид треугольника | Стороны треугольника | Катеты | Гипотенуза |
|---|---|---|---|
| Прямоугольный треугольник | Три | Прямые | Нет |
| Равносторонний треугольник | Три | Каждая сторона является катетом | Нет |
| Равнобедренный треугольник | Три | Два катета равны | Нет |
| Общий треугольник | Три | Могут быть разные | Нет |
Цель использования катетов в геометрии треугольника состоит в том, чтобы расширить наши знания о треугольниках и их свойствах. Они помогают нам понять форму и размер треугольника, а также вычислить различные характеристики треугольника, которые могут быть полезными в реальных ситуациях.
Определение катета
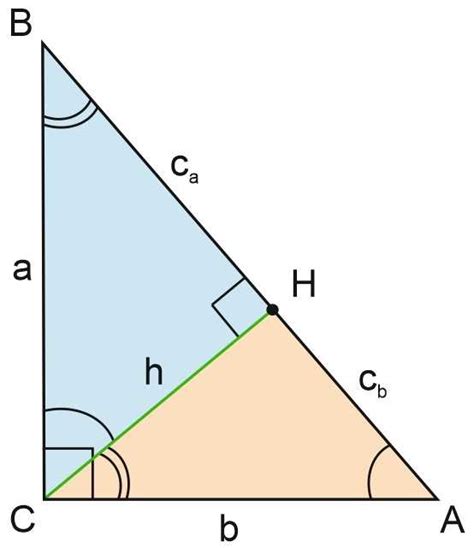
Катеты в прямоугольном треугольнике связаны согласно теореме Пифагора. Согласно этой теореме, квадрат длины гипотенузы равен сумме квадратов длин катетов: c² = a² + b².
Обозначения для катетов часто используют латинскими буквами a и b. Также вместо a и b можно использовать другие буквы, главное, чтобы обозначения были понятны и не вызывали путаницу.
Зная длину одного катета и длину гипотенузы, можно найти длину другого катета с помощью теоремы Пифагора или с использованием тригонометрических функций.
Особенности катетов в прямоугольном треугольнике
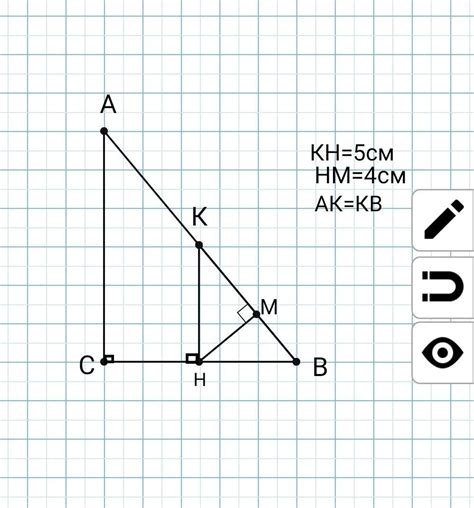
- Катеты перпендикулярны друг другу - они образуют прямой угол и лежат на противоположных сторонах гипотенузы.
- Катеты равны по длине - это следует из определения прямоугольного треугольника. Также можно сказать, что катеты являются равногранными катетами.
- Катеты служат основанием для определения гипотенузы, которая является наибольшей стороной прямоугольного треугольника.
- Катеты образуют прямоугольный треугольник, который используется в различных математических и геометрических задачах.
Знание особенностей катетов в прямоугольном треугольнике позволяет более полно понимать геометрические свойства этой фигуры и использовать его в решении задач различной сложности.
Роль и свойства катетов
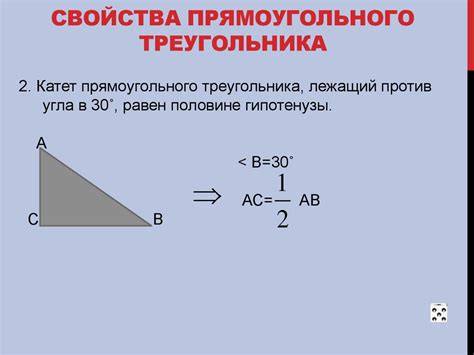
Одним из важных свойств катетов является их длина. Катеты всегда имеют положительное значение и могут быть разной длины. В прямоугольном треугольнике с катетами a и b гипотенуза c всегда больше каждого из катетов: c > a и c > b.
Также, катеты обладают следующим свойством: квадрат гипотенузы равен сумме квадратов катетов. Это выражается в известной формуле Пифагора: c² = a² + b². Это свойство позволяет нам находить длину одного из катетов или гипотенузы, зная длины других сторон треугольника.
Катеты также определяют углы треугольника. В прямоугольном треугольнике, катеты равны синусам острых углов. То есть для данного треугольника sin A = a / c и sin B = b / c, где A и B – острые углы, a и b – катеты, c – гипотенуза.
Катеты играют важную роль в решении задач на прямоугольные треугольники. Зная длины катетов, можно находить длину гипотенузы и углы треугольника, а также решать другие задачи, связанные с этой геометрической фигурой.
Длина катетов в зависимости от других сторон треугольника
Теорема Пифагора устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Таким образом, длина катетов может быть найдена как корень квадратный из разности квадрата гипотенузы и квадрата другого катета. Формула для нахождения длины катетов:
| Катет 1 | Катет 2 | Гипотенуза |
|---|---|---|
| √(гипотенуза² - катет²) | √(гипотенуза² - катет²) | гипотенуза |
Зная длину гипотенузы и одного катета, можно использовать формулу для вычисления второго катета. Обратное также верно - если известны длины двух катетов, можно найти длину гипотенузы по теореме Пифагора.
Знание длины катетов позволяет решать различные задачи в геометрии, в том числе находить площадь треугольника, его периметр и углы.
Закон синусов
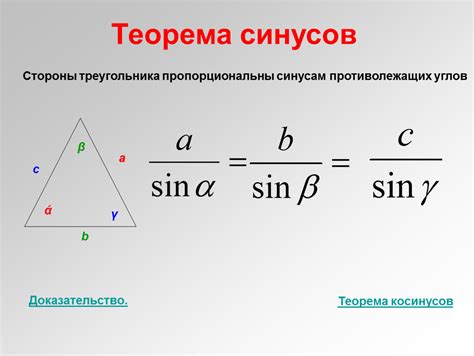
В треугольнике отношение любой стороны к синусу противолежащего ей угла равно отношению другой стороны к синусу противолежащего ей угла:
a/sin A = b/sin B = c/sin C
где a, b, c - стороны треугольника, A, B, C - противолежащие им углы.
Закон синусов позволяет решать треугольники, если известны две стороны и угол между ними, или три стороны треугольника и угол между двумя из них.
Важно помнить, что для применения закона синусов треугольник должен быть неравносторонним, то есть стороны и углы не должны быть равными друг другу.
Закон синусов удобен и применим в различных задачах геометрии, например, вычисление высоты треугольника, нахождение площади треугольника, нахождение углов треугольника по сторонам и другие.



