Синус минус первой степени - это математическая функция, которая вычисляет значение синуса аргумента, умноженное на -1. То есть, если значение синуса некоторого угла равно x, то значение синуса минус первой степени этого угла будет равно -x.
Знание синуса минус первой степени может быть полезно в различных областях, включая тригонометрию, физику, инженерные и научные расчеты. Например, при решении задач по оптике, электронике, механике или астрономии может возникнуть необходимость использования этой функции для точного вычисления значений углов.
Это математическое свойство синуса минус первой степени можно использовать для упрощения вычислений в некоторых случаях. Например, при работе с тригонометрическими формулами, где требуется выражение синуса аргумента с отрицательной степенью, можно использовать это свойство для перехода к положительной степени синуса и изменения знака результата.
Основные свойства синуса минус первой степени

Основные свойства синуса минус первой степени:
- Диапазон значений: синус минус первой степени может принимать любое значение между -1 и 1.
- Периодичность: функция синус минус первой степени имеет период 2π, то есть ее значения повторяются каждые 2π радиан или 360 градусов.
- Симметрия: синус минус первой степени симметричен относительно начала координат. Это означает, что если для некоторого значения x синус минус первой степени равен y, то для значения -x синус минус первой степени также равен -y.
- Пересечение с осями: синус минус первой степени пересекает ось x в точках, где угол равен 0, π, -π, 2π и т.д., и пересекает ось y в точке (0,0).
Использование синуса минус первой степени позволяет находить значения углов, синус которых известен, и позволяет анализировать колебательные явления, гармонические функции и другие математические модели.
Смысл синуса минус первой степени
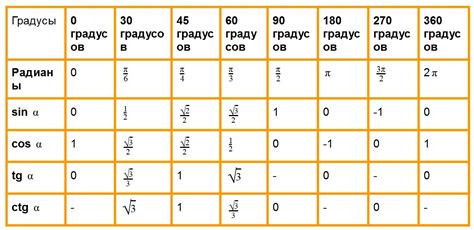
Основное значение синуса минус первой степени заключается в его способности представлять периодические процессы и колебания. Эта функция может принимать значения от -1 до 1 и в зависимости от угла входит в расчеты различных задач и моделей.
В геометрии синус минус первой степени используется при решении задач, связанных с определенными углами. Он позволяет находить значения углов в треугольниках, а также проводить дополнительные вычисления в угловых системах координат.
В физике синус минус первой степени применяется при решении задач, связанных с колебанием и волнами. Например, он используется для описания гармонических колебаний, звуковых волн, электромагнитных колебаний и других явлений в природе.
В технике синус минус первой степени широко применяется в электронике, радиотехнике, светотехнике и других областях. Он используется для анализа и моделирования сигналов, синтеза звука, расчёта электрических цепей и др.
Кроме того, синус минус первой степени входит в различные математические формулы и уравнения, что дает возможность осуществлять сложные вычисления и решать разнообразные задачи.
Специфика использования синуса минус первой степени
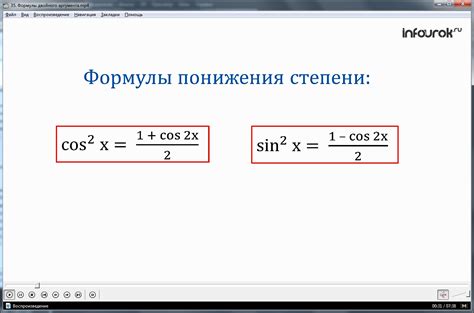
Синус минус первой степени может быть интерпретирован как обратная функция к обычному синусу. Другими словами, если угол а имеет синус равный b, то sin(-1)b будет равным а. Этот интересный факт делает синус минус первой степени важным инструментом для решения некоторых математических и физических задач.
В применении к геометрии, синус минус первой степени позволяет нам находить значение угла, если известен его синус. Это может быть полезно, например, при решении задач по тригонометрии, в которых требуется найти угол по заданным сторонам треугольника.
В физике синус минус первой степени может использоваться для нахождения начального угла при отражении света от поверхности или для решения задач, касающихся колебаний и волн.
Если использовать синус минус первой степени в качестве аргумента для функций научного калькулятора, необходимо учесть, что обычный синус оперирует значениями от -1 до 1, в то время как синус минус первой степени может принимать значения от -∞ до ∞. Поэтому, при использовании этой функции, особое внимание следует уделить правильному выбору границ и интерпретации результатов.
График синуса минус первой степени
Синус минус первой степени, обозначаемый как sin(-1), представляет собой обратную функцию к синусу. На графике данной функции каждая точка представляет значение синуса минус первой степени от аргумента.
График синуса минус первой степени симметричен по оси OX и принимает значения в диапазоне от -π/2 до π/2. Наибольшее значение равно 1 при аргументе 0, а наименьшее значение равно -1 при аргументе π/2 или -π/2.
Синус минус первой степени может быть выражен через обратную функцию arcsin(x) или asin(x), где x - значение синуса минус первой степени. Формула выглядит следующим образом: sin(-1) = arcsin(x).
График синуса минус первой степени имеет форму плавно меняющейся кривой, период которой равен 2π. Также можно заметить, что график проходит через точку (0, 0), что означает, что sin(-1) при аргументе 0 равен 0.
Использование графика синуса минус первой степени помогает в анализе и решении различных математических проблем, а также может быть полезно в физике, инженерии и других науках.
Расчет значения синуса минус первой степени
Синус минус первой степени (sin(-1)) представляет собой обратную функцию синуса. Чтобы рассчитать значение синуса минус первой степени для заданного угла, необходимо следовать определенному алгоритму.
Алгоритм расчета значения синуса минус первой степени:
- Найдите значение угла, для которого нужно рассчитать синус минус первой степени.
- Проверьте, что значение угла лежит в диапазоне от -1 до 1. Если значение угла выходит за этот диапазон, значит синус минус первой степени не существует.
- Если значение угла находится в диапазоне от -1 до 1, примените обратную функцию синуса к этому значению.
- Результатом будет значение синуса минус первой степени.
Пример расчета значения синуса минус первой степени:
| Значение угла | Значение синуса минус первой степени |
|---|---|
| -0.5 | -30° |
| 0 | 0° |
| 0.5 | 30° |
Таким образом, расчет значения синуса минус первой степени зависит от заданного значения угла и его соответствия указанному диапазону. Важно следовать алгоритму и убедиться, что угол находится в допустимом диапазоне для успешного расчета значения синуса минус первой степени.
Свойства синуса минус первой степени в математическом анализе

Основное свойство синуса минус первой степени - это его способность находить угол, значение синуса которого равно заданному числу. То есть, если sin(theta) = x, то arcsin(x) = theta. Отсюда следует, что значение аргумента arcsin(x) находится в диапазоне [-pi/2, pi/2], где pi/2 - половина периода функции синуса.
Другое важное свойство синуса минус первой степени - это его конечные значения на отрезке [-1, 1]. Если x принадлежит к этому отрезку, то arcsin(x) также принимает значение из этого отрезка, то есть [-pi/2, pi/2]. Если x не принадлежит отрезку [-1, 1], то arcsin(x) не имеет действительных значений.
Свойство синуса минус первой степени, которое нельзя игнорировать в математическом анализе, связано с его однозначностью. Так как функция синуса - периодическая функция, то существует бесконечное количество значений угла синуса, равное заданному числу. Однако, функция синус минус первой степени определена таким образом, чтобы возвращать только одно значение аргумента theta, такое что sin(theta) = x, и значение этого аргумента находится в пределах от [-pi/2, pi/2]. Возможны другие обозначения, которые гарантируют однозначность, такие как sin-1(x) или arcsin(x).
Важно отметить, что свойства синуса минус первой степени применяются не только в математическом анализе, но и в других областях, таких как физика, инженерия и компьютерная графика. Знание этих свойств позволяет решать различные задачи, связанные с тригонометрическими функциями и углами.



