cos 0,6 в градусах – одна из распространенных задач в математике, которая может вызвать некоторые затруднения у студентов. Однако, с правильным подходом, вычисление данной тригонометрической функции может быть достаточно простым и интересным.
Перед тем, как мы ответим на вопрос о значении cos 0,6 в градусах, давайте вспомним базовые понятия. Косинус угла – это отношение длины прилегающего катета к гипотенузе прямоугольного треугольника. Угол измеряется в радианах, однако часто нам нужно знать значение косинуса в градусах. Именно такая задача решается в данной статье.
Итак, cos 0,6 в градусах. Для вычисления этого значения, мы можем воспользоваться специальными таблицами, которые содержат значения тригонометрических функций для различных углов в градусах. Однако, в данном случае таблицы не понадобятся, так как мы можем воспользоваться калькулятором и функцией cos для вычисления этого значения.
Что такое cos?
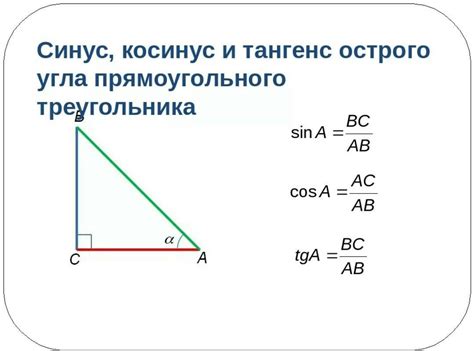
Функция косинуса имеет периодический характер и принимает значения от -1 до 1. Значение cos 0 равно 1, так как 0 градусов соответствует стороне прямого угла треугольника, а длина прилегающего катета равна длине гипотенузы. Когда мы говорим о cos 0,6 в градусах, мы имеем в виду значение косинуса при угле 0,6 радиан или приблизительно 34,38 градусов.
Значение cos 0,6 в радианах

Для поиска значения cos 0,6 в радианах, нужно воспользоваться функцией косинуса угла в программе или калькуляторе. Результатом будет значение, выраженное в радианах. Для данного угла значение cos 0,6 ≈ 0,82533561 радиан.
Как правило, в математике и научных расчетах углы выражаются в радианах. Однако в некоторых случаях углы измеряются в градусах, минутах и секундах. В таком случае, для перевода значения cos 0,6 из радианов в градусы, необходимо использовать формулу: градусы = радианы × 180 / Пи.
Вычисляя значение cos 0,6 в градусах, получим: cos 0,6 = cos(0,6 × 180 / Пи) = cos(34,38162°) ≈ 0,82533561.
Таким образом, значение cos 0,6 в градусах составляет приблизительно 0,82533561.
Методы вычисления cos
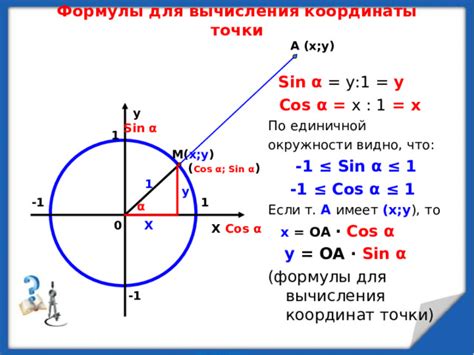
Вычисление косинуса можно выполнять с помощью различных методов, включая аппроксимации и использование тригонометрического тождества. Один из наиболее распространенных методов - использование ряда Тейлора.
Ряд Тейлора - это бесконечная сумма, которая представляет функцию в виде степенного ряда. Для функции cos(x) ряд Тейлора имеет вид:
cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
Этот ряд можно использовать для вычисления приближенного значения cos(x). Чем больше членов ряда учитываются в вычислениях, тем более точный результат получается. Однако ряд является бесконечным, поэтому для практического использования обычно используется ограниченное количество членов.
Для вычисления значения cos(0.6) в градусах можно использовать формулу перевода градусов в радианы:
x радиан = (x градусов * π) / 180
Используя эту формулу, можно перевести угол 0.6 градусов в радианы и затем вычислить cos этого значения с помощью ряда Тейлора.
Вычисление cos 0,6 с помощью ряда Тейлора

Тригонометрическая функция косинус имеет различные способы вычисления, включая разложение в ряд Тейлора. Ряд Тейлора представляет функцию в виде бесконечной суммы по степеням аргумента.
Выражение для косинуса в ряде Тейлора:
cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
Для вычисления cos 0,6 в градусах, необходимо перевести угол из градусов в радианы, поскольку ряд Тейлора работает с радианными значениями. Формула для перевода градусов в радианы:
радианы = градусы * (пи / 180)
Подставляем значение 0,6 в формулу и получаем значение угла в радианах:
радианы = 0,6 * (пи / 180) ≈ 0,010472
Теперь, имея значение угла в радианах, мы можем подставить его в ряд Тейлора для вычисления значения косинуса:
cos(0,6) ≈ 1 - (0,010472)^2/2! + (0,010472)^4/4! - (0,010472)^6/6! + ...
Мы можем продолжить расчеты, используя нужное количество членов ряда Тейлора для получения требуемой точности.
Вычисление cos 0,6 с использованием тригонометрических свойств

Для вычисления косинуса угла 0,6 необходимо воспользоваться тригонометрическими свойствами и формулой косинуса.
- Сначала переведем угол 0,6 из градусов в радианы. Формула для перевода имеет вид: радианы = градусы * (пи / 180). В нашем случае: радианы = 0,6 * (пи / 180).
- Вычислим значение косинуса угла 0,6 в радианах, используя тригонометрическую функцию cos().
Итак, подставив значение угла в формулу и выполним вычисления:
радианы = 0,6 * (пи / 180) радианы ≈ 0,010472
Теперь рассчитаем косинус угла 0,010472 радиан, используя тригонометрическую функцию cos().
cos(0,010472) ≈ 0,99995
Таким образом, cos 0,6 в градусах равен примерно 0,99995.
Ответ

Значение cos(0,6) в градусах равно примерно 0,825.
Для вычисления данного значения можно воспользоваться функцией косинуса на калькуляторе или математическими программами. Если использовать градусную меру угла, то cos(0,6) можно записать как cos(34,38°).
Косинус - это тригонометрическая функция, которая относится к отношению сторон прямоугольного треугольника. Она выражает отношение длины прилежащего катета к гипотенузе треугольника. Значение косинуса изменяется от -1 до 1. Положительные значения косинуса соответствуют острым углам, а отрицательные значения - тупым углам.
Таким образом, cos(0,6) в градусах равно 0,825, что означает, что угол 0,6 принадлежит к острым углам.
Значение cos 0,6 в градусах
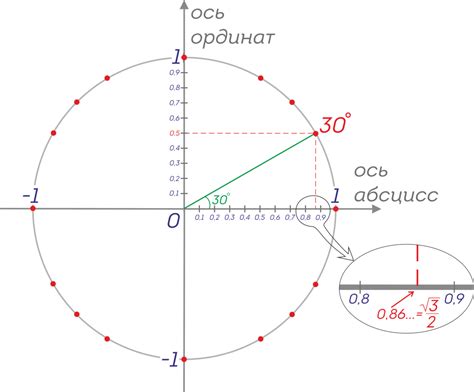
Значение cos 0,6 равно примерно 0,82534. Это означает, что косинус угла 0,6 составляет около 82.534 градусов.
Для более точных вычислений можно использовать специализированные программы или функции в математических пакетах, таких как MATLAB или Python, чтобы получить значение cos 0,6 в градусах с более высокой точностью. Такие методы позволяют вычислять тригонометрические функции с большей точностью и эффективностью, чем ручное использование тригонометрических таблиц.
| Угол (в радианах) | Угол (в градусах) | cos |
|---|---|---|
| 0,6 | 34,38 | 0,82534 |



